RSA加密算法计算原理｜RSA algorithm computation principles

一、RSA简介 | Introduction to RSA

RSA是一种非对称加密算法，由Rivest、Shamir和Adleman三人于1977年提出。该算法的核心思想是：加密和解密分别使用不同的密钥——公钥和私钥。其中公钥公开用于加密，私钥保密用于解密。

RSA is an asymmetric encryption algorithm proposed by Rivest, Shamir, and Adleman in 1977. The core idea of RSA is to use a pair of different keys for encryption and decryption—a public key and a private key. The public key is shared openly for encryption, while the private key is kept secret for decryption.

二、RSA算法的计算过程 | Computational Steps of RSA

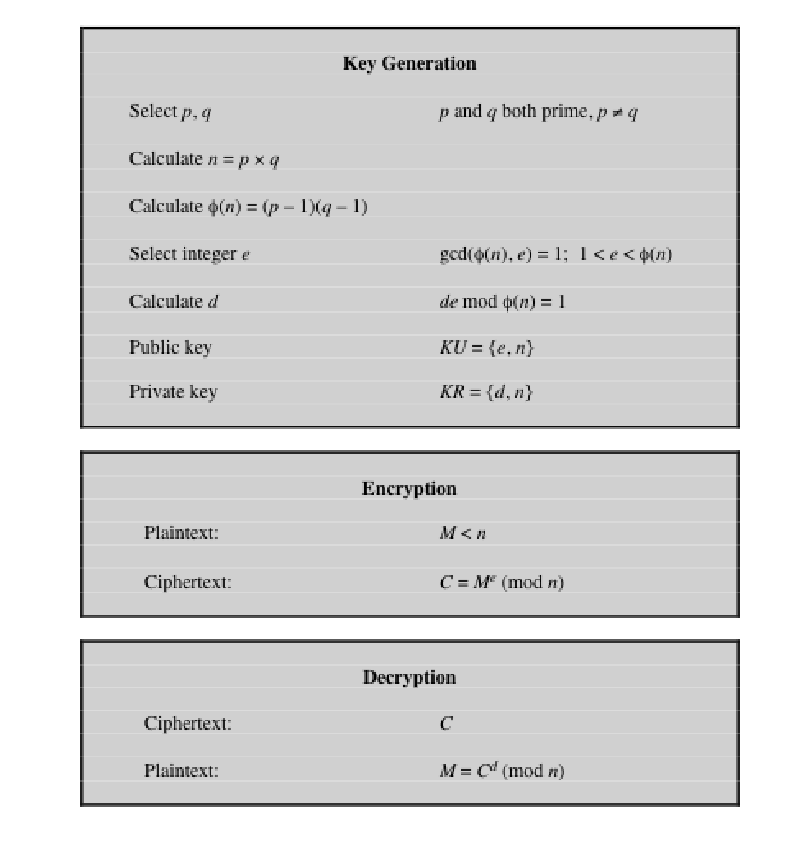
1. 密钥生成（Key Generation）

• 选择两个大素数 p 和 q，且 p≠q
  Select two large prime numbers p and q, where p≠q

• 计算 n=p×q
  Compute n=p×q

• 计算欧拉函数 φ(n)=(p−1)(q−1)
  Compute Euler’s totient function φ(n)=(p−1)(q−1)

• 选择整数 e，满足 1<e<φ(n)，且 gcd⁡(e,φ(n))=1
  Select an integer e such that 1<e<φ(n) and gcd⁡(e,φ(n))=1

• 求解 d，满足 d⋅e≡1(mod  φ(n))
  Compute d such that d⋅e≡1mod  φ(n)

• 公钥为 (e,n)，私钥为 (d,n)
  The public key is (e,n), and the private key is (d,n)

三、加密与解密过程 | Encryption and Decryption

加密（Encryption）

• 明文 P 满足 P<n
  Plaintext P such that P<n

• 密文 C≡P^e mod  n
  Ciphertext C≡P^e mod  n

解密（Decryption）

• 明文 P≡C^d mod  n
  Plaintext P≡C^d mod  n

四、RSA算法例子1 | Example 1

已知：

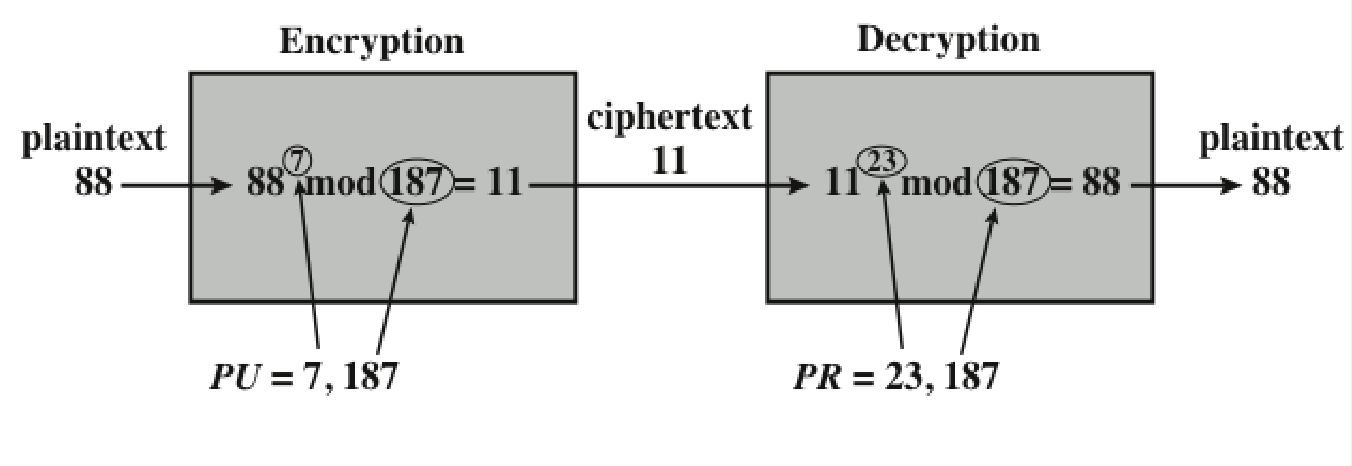
• 公钥 e=7,n=187

• 私钥 d=23,n=187

• 明文 P=88

加密过程：

C=88⁷ mod  187 = 11

解密过程：

P=11²³ mod  187 = 88

通过加密和解密可以看到，明文得以还原，验证了RSA算法的有效性。

五、RSA算法例子2 | Example 2

1. 密钥生成

• p=3，q=11

• n=3×11=33

• φ(n)=(3−1)(11−1)=2×10=20

• 选择 e=7，满足 gcd⁡(7,20)=1

接下来求 d，满足：

d⋅7 ≡ 1 mod  20

采用试探法：

• 7⋅1=7mod  20=7≠1

• 7⋅2=14mod  20=14≠1

• 7⋅3=21mod  20=1⇒ d = 3

也可以使用扩展欧几里得算法：

1. 20=2⋅7+6

2. 7=1⋅6+1

3. 6=6⋅1+0

回代求得：

1=3⋅7−1⋅20⇒ d=3

因此，公钥为 (e=7,n=33)，私钥为 (d=3,n=33)

2. 加密过程

明文 P=4

C=4⁷ mod  33 = 16384 mod  33 = 16

3. 解密过程

密文 C=31

P=16³ mod  33 = 4096 mod  33 = 4

明文成功还原。

六、RSA中的安全性问题 | Security Considerations

RSA的安全性依赖于大整数分解的困难性，即从n推导出 p 和 q 是不可行的。当密钥长度足够大时，这一任务在当前计算条件下是无法完成的。

但RSA并非绝对安全，它可能受到以下几种攻击方式：

• 数学攻击（Mathematical attacks）：尝试通过算法改进来因式分解大整数

• 时间攻击（Timing attacks）：通过测量解密操作的时间来推测私钥

• 选择密文攻击（Chosen ciphertext attacks）：通过特制的密文引导解密端泄露信息

在实际应用中，通常会配合填充方案（如OAEP）来增强RSA的安全性。

七、总结 | Conclusion

RSA算法的基本流程如下：

1. 生成两个素数 p,q

2. 计算 n=pq、φ(n)

3. 选择 e，求得 d

4. 利用公钥加密：C=P^e mod  n

5. 利用私钥解密：P=C^d mod  n

RSA作为一种经典的公钥密码体制，在数字签名、加密通信、身份认证等方面发挥着重要作用。

RSA is a cornerstone of modern cryptography, providing robust solutions for secure communication, digital signatures, and authentication.