一、偏差和方差的拟合对比

这张图片通过房价预测(Price vs. Size)的回归问题,展示了不同多项式回归模型的拟合情况,重点对比了高偏差(欠拟合)和理想拟合和高方差(过拟合)的模型表现,并涉及训练误差(Jtrain)和交叉验证误差(Jcv)的变化。
1. 左侧:高偏差(欠拟合)模型
模型方程:

(线性回归,多项式阶数 d=1)
关键观察:
训练误差(Jtrain)高:模型过于简单,无法拟合数据的真实趋势(如二次关系)。
交叉验证误差(Jcv)高:在验证集上表现同样差,说明模型泛化能力弱。
尝试调整模型复杂度(提高 d):
当 d=2 时,误差仍然高 → 说明模型仍欠拟合(可能因特征不足或模型选择不当)。
结论:模型欠拟合,需要增加特征或使用更复杂的模型(如 d≥2)。
2. 中间:理想拟合模型
模型方程:

(二次多项式回归,多项式阶数 d=2)
关键观察:
训练误差(Jtrain)低:模型能够较好拟合训练数据。
交叉验证误差(Jcv)低:在验证集上表现良好,泛化能力强。
结论:模型复杂度恰到好处(d=2),平衡了偏差和方差。
3. 右侧:高方差(过拟合)模型
模型方程:

关键观察:
训练误差(Jtrain)极低:模型完美拟合训练数据(甚至噪声)。
交叉验证误差(Jcv)很高:泛化能力差,验证集表现大幅下降。
结论:模型过拟合,需要减少特征或使用更简单的模型(如 d≦4)。
总结图示的核心信息
二、偏差与方差:误差曲线诊断

这张图片展示了训练误差(Jtrain)和交叉验证误差(Jcv)随多项式阶数(degree of polynomial)变化的趋势,用于诊断模型的偏差(Bias)和方差(Variance)。
关键元素说明
横轴(degree of polynomial):
表示模型复杂度(多项式阶数 d),从低(如 d=1)到高(如 d=4 或更高)。
纵轴(误差值):
Jtrain(W,b):训练集误差,反映模型对训练数据的拟合程度。
Jcv(W,b):交叉验证集误差,反映模型泛化能力。
曲线趋势(图中未绘制但隐含):
低阶(如 d=1):
Jtrain 和 Jcv 均高 → 高偏差(欠拟合)。
中阶(如 d=2):
Jtrain 和 Jcv 均较低且接近 → 理想拟合。
高阶(如 d≥4):
Jtrain 极低,Jcv 显著升高 → 高方差(过拟合)。
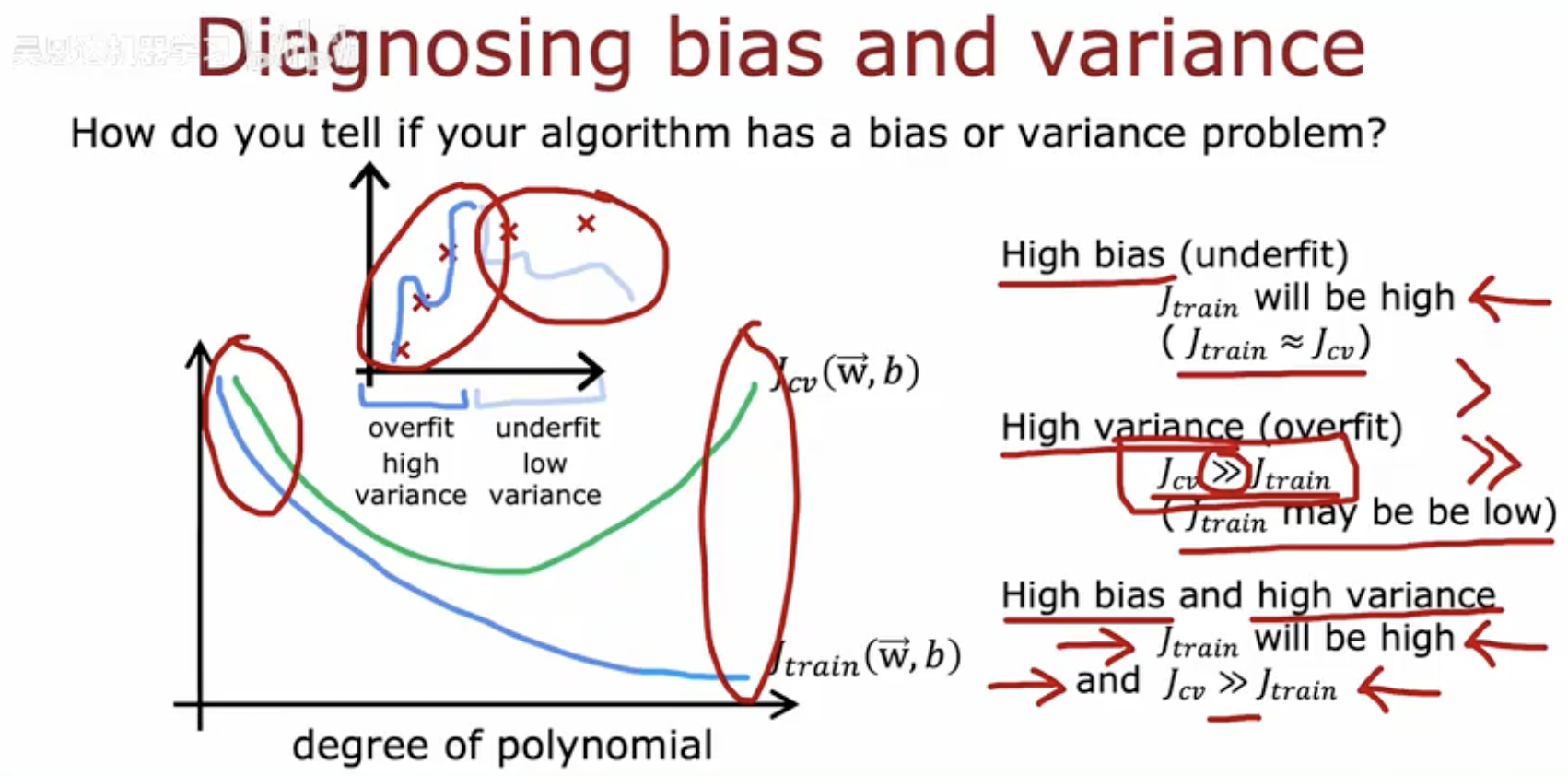
这张图片系统性地展示了如何通过训练误差(J_train)和交叉验证误差(J_cv)来判断算法存在高偏差(欠拟合)还是高方差(过拟合)问题,以及两者的组合情况。
核心诊断逻辑
高偏差(欠拟合)特征:
Jtrain 很高(模型无法拟合训练数据)
Jcv 也很高(泛化能力差)
典型表现:简单模型(如低阶多项式)
高方差(过拟合)特征:
Jtrain 可能很低(完美拟合训练数据)
Jcv 显著高于 Jtrain(泛化能力差)
典型表现:复杂模型(如高阶多项式)
高偏差+高方差特殊情况:
Jtrain 很高(欠拟合训练数据)
Jcv 比 Jtrain 更高(同时存在泛化问题)
典型场景:模型既不够灵活又过度适应噪声
诊断步骤
比较Jtrain和Jcv的相对大小
观察两者随模型复杂度变化的趋势
根据表格中的特征匹配问题类型
