一、前向传播简介

前向传播是神经网络中数据从输入层流向输出层的过程，每一层对输入数据进行加权求和并通过激活函数转换，最终得到预测结果。通俗来说，就像“信息在神经网络中一步步前向传递，每一层加工一点，最后给出答案”。

通俗理解

想象你在一家汉堡店点餐：

1. 输入层：你选择食材（输入数据）。

2. 隐藏层：厨师按食谱（权重）加工食材，并加调料（偏置和激活函数）。

3. 输出层：最终做出汉堡（预测结果）。
   前向传播就是“按顺序做汉堡”的过程！

二、前向传播过程

这张图片展示了一个咖啡烘焙模型（coffee roasting model）的前向传播（forward prop）过程，使用NumPy实现了一个简单的两层神经网络。以下是关键点解析：

1. 输入数据

• x = np.array([200, 17])
  输入特征向量，表示咖啡烘焙的时长（200秒）和温度（17°C）。

2. 第一层（隐藏层）的计算

• 3个神经元，分别计算 a₁^[1],a₂^[1],a₃^[1]：

  • 每个神经元的计算分为两步：

    1. 线性变换：z=W⋅x+b

    2. 激活函数：a=g(z)（图中 g 为 sigmoid）。

  • 示例（第一个神经元）：

    python

    w1_1 = np.array([1, 2])  # 权重
    b1_1 = np.array([-1])     # 偏置
    z1_1 = np.dot(w1_1, x) + b1_1  # 线性变换
    a1_1 = sigmoid(z1_1)      # 激活输出

3. 第二层（输出层）的计算

• 1个神经元，计算 a₁^[2]：

  • 输入是第一层的输出 a^[1]=[a1_1, a1_2, a1_3]。

  • 公式与第一层类似，但权重和偏置不同：

    python

    w2_1 = np.array([-7, 8])  # 注意维度与第一层输出匹配
    b2_1 = np.array([3])
    z2_1 = np.dot(w2_1, a1) + b2_1
    a2_1 = sigmoid(z2_1)

4. 符号说明

• 上标 [1]、[2] 表示层数，下标 _1、_2 表示神经元序号。

• 公式中的 x 和 a ^[1] 是输入和上一层的输出向量。

三、在NumPy中实现神经网络的前向传播

这张图片展示了如何在 NumPy 中实现神经网络的前向传播（Forward Propagation），包含一个通用的 dense 层函数和一个 sequential 顺序模型。以下是关键点解析：

1. dense 函数（单层计算）

• 功能：实现一个全连接层的前向传播。

• 参数：

  • a_in：输入向量（上一层的输出）。

  • W：权重矩阵（shape = (输入维度, 单元数)）。

  • b：偏置向量。

  • g：激活函数（如 sigmoid）。

• 计算步骤：

  1. 对每个神经元 j，提取权重列向量 W[:,j]。

  2. 计算线性变换：z = np.dot(w, a_in) + b[j]。

  3. 应用激活函数：a_out[j] = g(z)。

示例：

python

a_out = dense(a_in, W, b, sigmoid)  # 输出激活值向量

2. sequential 函数（多层模型）

• 功能：按顺序堆叠多个 dense 层（4层）。

• 流程：

  python

  a1 = dense(x, W1, b1)   # 第1层
  a2 = dense(a1, W2, b2)  # 第2层
  a3 = dense(a2, W3, b3)  # 第3层
  a4 = dense(a3, W4, b4)  # 第4层
  f_x = a4                # 最终输出

3. 权重与偏置的定义

• 权重矩阵 W：

  • 第一层的权重（示例）：

    

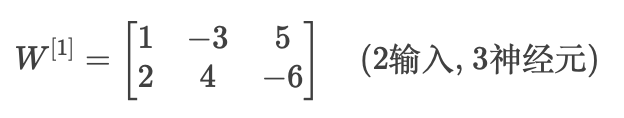
    python

    W = np.array([[1, -3, 5], [2, 4, -6]])  # shape (2, 3)

• 偏置向量 b：

  python

  b = np.array([-1, 1, 2])  # 对应3个神经元

4. 输入数据

• 初始输入向量：

  

  python

  a_in = np.array([-2, 4])

5. 符号说明

• 大写 W 表示权重矩阵，小写 b 表示偏置向量。

• 上标 [l] 表示层号（如 W^{[1]} 是第一层权重）。