一、线性回归的含义

线性回归（Linear Regression）是统计学和机器学习中最基础、最常用的预测模型之一，用于分析因变量（目标变量）与一个或多个自变量（特征变量）之间的线性关系。其核心思想是通过拟合一条最佳直线（或超平面）来描述变量之间的关系，并据此进行预测。

通俗理解：
想象你在卖冰淇淋，发现一个规律：天气越热，卖出的冰淇淋越多。你想量化这个关系，比如：
气温每升高1℃，大概会多卖多少支？
如果明天35℃，预测能卖多少？
线性回归就是帮你找一条“最合适”的直线，来描述这种规律。

例子(一)

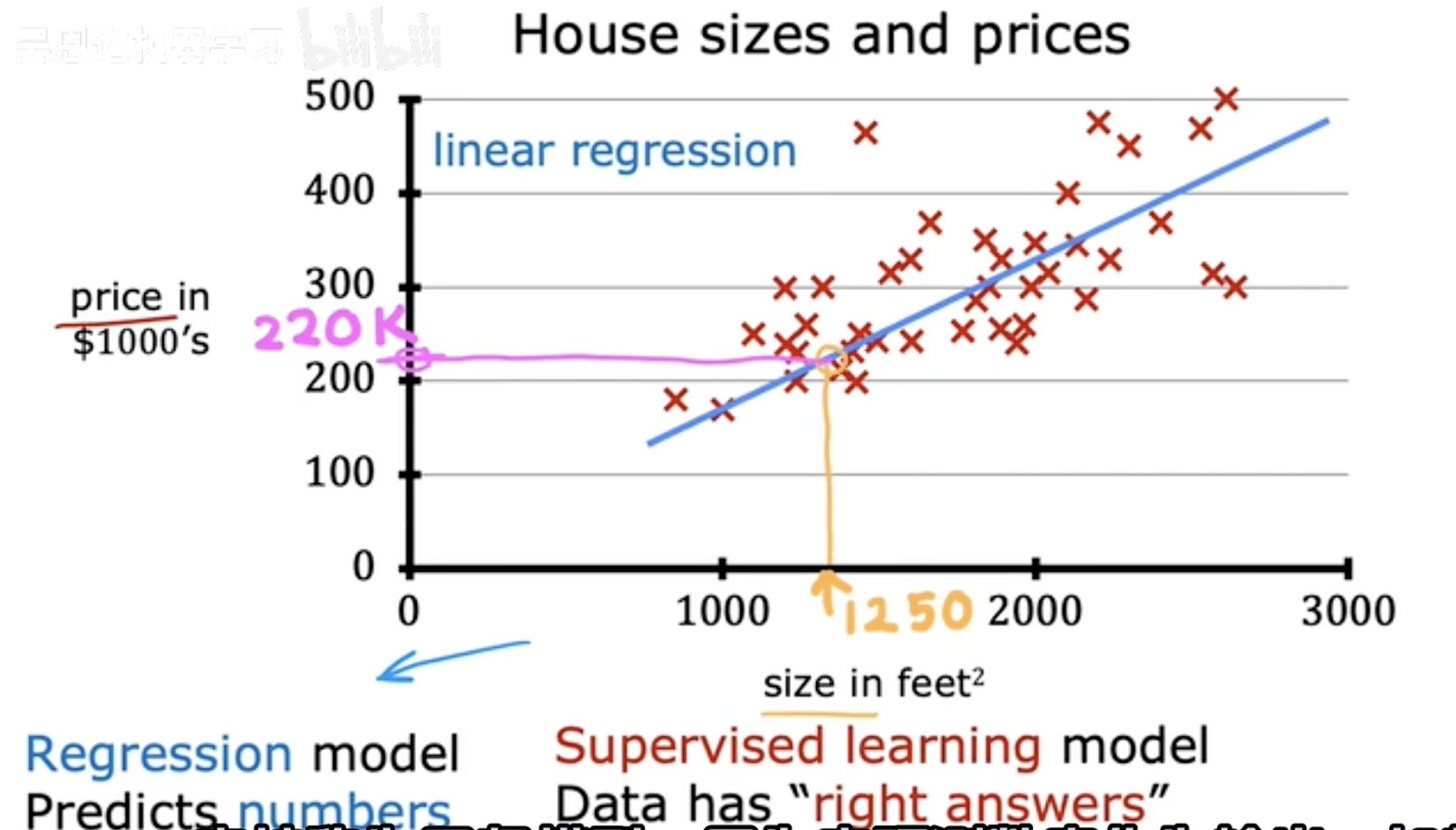
线性回归(图1).png

数据点：
- 每个点代表一套房屋，横坐标是它的面积（X），纵坐标是它的价格（Y，单位：$1000）。
- 比如右上角的点：面积大，价格高；左下角的点：面积小，价格低。
蓝色斜线（回归模型）：
- 这是通过数据自动拟合的“趋势线”，用来总结面积和价格的关系。
- 线的方向：向右上方延伸 → 面积越大，价格越高（正相关）。
- 线的意义：
  - 如果新房子面积是图中某个值，直接垂直向上找到线上的点，就是预测价格。
“Supervised Learning”：
- 因为图中每个点都有已知的真实价格（即“right answers”），模型是通过学习这些正确答案总结规律的。
“Predicts numbers”：
- 这条线的核心功能：输入面积，输出一个具体的预测价格数字（比如面积=1250平方英尺 → 价格≈$220,000）。

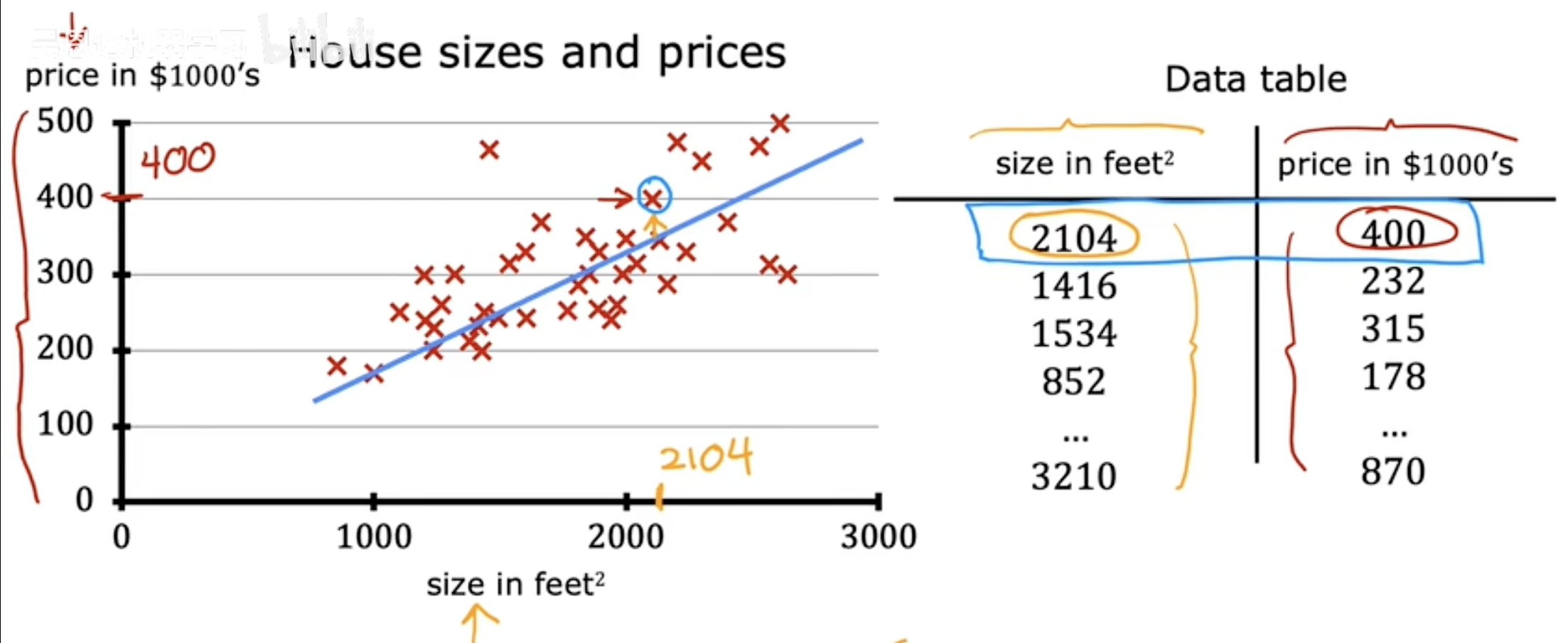
线性回归(图2).png

例子(二)

线性回归(图3).png

训练集是什么

就是用来教电脑学习的数据表格（图中左边的数字表格）
比如这个表格里记录了47套房子的面积和价格（实际只显示了前4套和最后1套）

重要术语解释

x（输入）：房子的面积（单位：平方英尺）
y（输出）：房子的价格（单位：千美元）
m：总共有47条数据（因为有第47条记录）

“i”符号说明

x⁽¹⁾=2104：表示"第一条数据的面积是2104平方英尺"
y⁽¹⁾=400：表示"第一条数据的价格是40万美元"
(x⁽ⁱ⁾,y⁽ⁱ⁾)：表示"任意一条数据"

表格内容
每一行就是一套房子的信息：
第一列是编号，第二列是面积(x)，第三列是价格(y)
比如第4套房：852平方英尺，17.8万美元
特别注意

价格单位是"千美元"，所以400=40万
上标的(1)、(i)只是编号，不是数学运算

二、机器学习模型训练过程

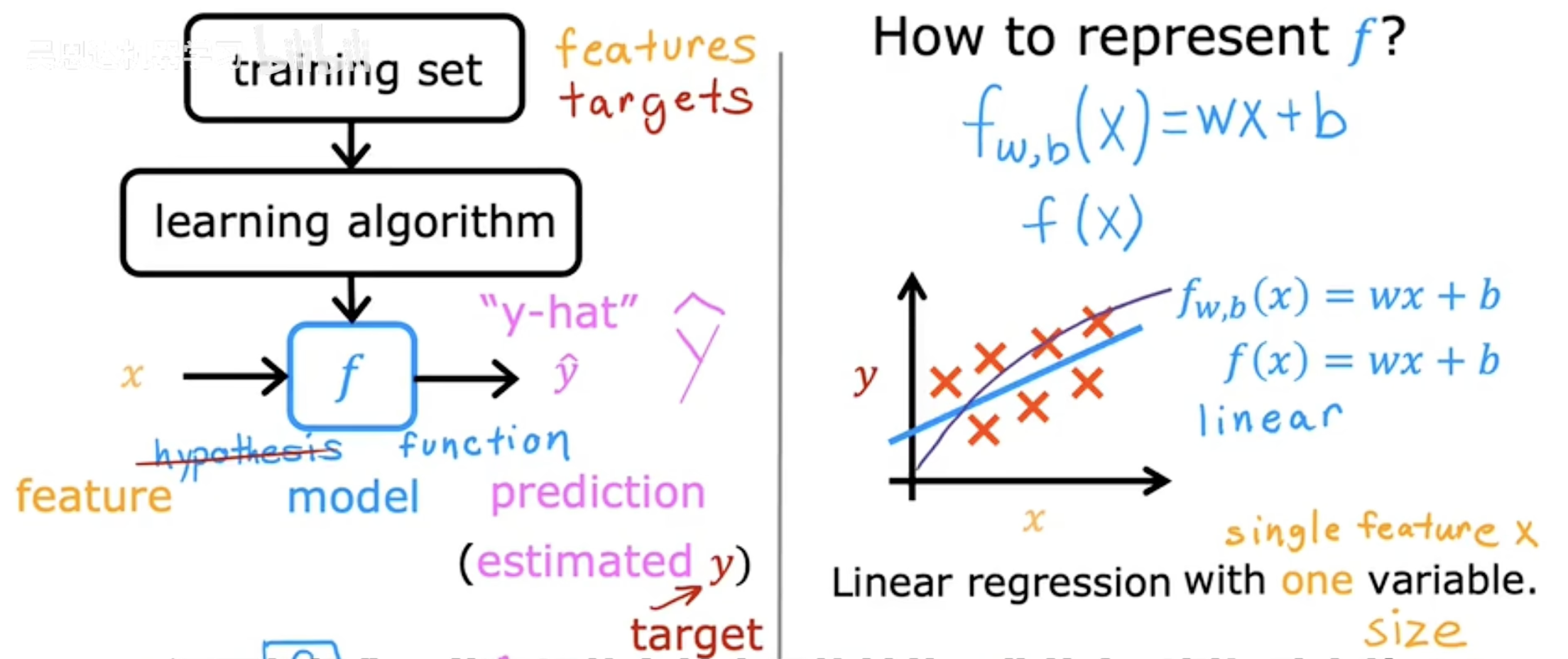
线性回归(图4).png

1. 核心流程图解

图片展示的是机器学习模型的训练过程：

text

[训练数据] → [学习算法] → [预测函数f] → [预测结果ŷ]

输入 (x)：房屋面积（特征）
输出 (ŷ)：预测价格（带小帽子的y）
f(x)：连接x和ŷ的"魔法公式"

2. 关键概念详解

(1) ŷ (y-hat) 是什么？

正式定义：模型对真实价格y的预测值（estimated y）
为什么加"帽子"：
就像天气预报的"预测温度"≠实际温度，ŷ是模型猜的价格，y才是真实成交价。
例子：
如果模型预测100㎡房子卖￥200万（ŷ=200），实际成交￥210万（y=210），误差就是10万。

(2) 假设函数 (Hypothesis Function)

数学表示：
f_w,b(x)=wx+b
或简写 f(x)=wx+b
每个部分的含义：
- w（weight）：斜率，代表"每平米值多少钱"
  （如w=0.5 → 每㎡增值￥5000）
- b（bias）：截距，代表"白送的基础价格"
  （如b=50 → 即使0㎡也要收￥50万，可能是土地成本）
- x：输入的特征值（面积）
为什么叫"假设"：
因为这是模型对现实规律的猜测，需要数据验证。

(3) 线性回归的特性

线性：公式画出来是一条直线
（如果数据是曲线，就需要多项式回归）
单变量：只有一个输入特征x（面积）
（如果有多个特征如卧室数，就叫多元线性回归）

3. 学习算法的工作

目标是找到最优的w和b，让预测误差最小。具体步骤：

初始化：随机给w和b赋值（比如w=0，b=0）
计算预测值：用当前w,b计算所有房子的ŷ
计算误差：比较ŷ和真实y的差距（常用均方误差）
调整参数：通过梯度下降等算法微调w和b
重复：直到误差无法继续减小

三、一元线性回归代码分析

（1. 先构造了表格来展示数据）

import pandas as pd # 数据处理库 读取csv文件，表格 2 筛选排序 3 计算统计量（平均数，最大值，标准差）
import matplotlib.pyplot as plt # 绘图工具库，可以用来画折线图，柱状图，饼图等
import seaborn as sns # 更高级的可视化库，用于画散点图，热力图，箱线图，分布图等。

# 一元线性回归：就是只包含一个自变量，且该自变量与因变量之间的关系是线性关系。
# 例如通过广告费这一个自变量来预测销量，就属于一元线性回归分析。

# 构造数据
data = {
    "人工成本": [5000, 6500, 7000, 6000, 10000, 3800, 6000, 1500, 9000, 9400,
               3000, 4500, 7000, 7500, 4500, 6000, 2000, 7800, 6500, 4500],
    "产量(公斤)": [200, 400, 500, 300, 800, 150, 360, 50, 750, 780,
               110, 160, 520, 560, 145, 350, 80, 600, 367, 157]
}

data = pd.DataFrame(data)
data

线性回归(图5).png

（2. 利用数据构造图）

# 选中自变量与因变量的数据，x为自变量，y为因变量
# x是自变量（输入）
# y是因变量（输出）

x=data[['人工成本']]
y=data[['产量(公斤)']]


# 查看变量的相关性（相关系数矩阵）
# 确定线性回归分析的类型——图3
corr=data.corr() # 计算皮尔逊相关系数， 值是在 -1，1之间，越接近1 说明正相关越强
print(corr)
# 绘制散点图——图1
plt.rcParams['font.sans-serif']=['Arial Unicode MS']  # 用中文字体显示
plt.rcParams['axes.unicode_minus']=False
# 成本 vs 产量
sns.pairplot(data,x_vars=['人工成本'],y_vars='产量(公斤)')
plt.show()

线性回归(图6).png

（3. 建立回归分析模型）

#建立回归分析模型
from sklearn.linear_model import LinearRegression # 线性回归 
Model=LinearRegression()  

Model.fit(x,y) # 训练数据拟合模型


#检验线性回归分析模型的拟合程度
#拟合评分 score()返回决定系数 R的平方，来衡量模型的好坏，=1 完全拟合，<0.5说明拟合的不好，>0.8说明很好
score=Model.score(x,y)
print(score)

拟合评分
0.9318449405268809

（4. 绘制拟合成果图）

# 绘制拟合成果图
# king = reg 添加拟合线和95%的置信区间
sns.pairplot(data,x_vars=['人工成本'],y_vars='产量(公斤)',kind='reg')# king参数可添加一条最佳拟合直线和95%的置信带，从而更直观的展示模型的拟合程度
plt.show()

线性回归(图7).png

（5.进行预测）

# 预测
y=Model.predict([[6000]])
print(y)

[[379.49546178]]

（设x=6000，预测结果y=379.49546178）

整体流程：

"""

数据准备(拆分x,y) --> 相关性分析(.corr()) --->散点图 ---> 线性回归模型建模(.fit) -->模型评估(score()) -->结果可视化 ---> 预测 

"""

四、多元线性回归代码分析

多元线性回归流程和一元线性回归流程大抵差不多。