一、代价函数的含义
代价函数(Cost Function),也称为损失函数(Loss Function)或目标函数(Objective Function),是机器学习中衡量模型预测结果与真实值之间差异的数学函数。它如同指南针一般,为模型优化指明方向,是训练任何机器学习模型的核心组成部分。
在机器学习的世界里,我们通过不断调整模型参数来最小化代价函数的值,这个过程就是模型"学习"的本质。代价函数的选择直接影响着模型的训练效果和最终性能,不同的机器学习问题需要不同类型的代价函数来引导模型朝着正确的方向优化。
二、理解 w 和 b——以房价预测为例
(一)训练数据与模型定义

1. 训练数据集(Training set)
特征(features):房屋面积(平方英尺),记为 x。
示例值:2104, 1416, 1534, 852, ...
目标值(targets):房屋价格(千美元),记为 y。
示例值:460, 232, 315, 178, ...
表格形式:
2. 模型定义
线性模型:fw,b(x)=wx+b
x:输入特征(房屋面积)。
w:权重(weight),控制特征对预测的影响程度。
b:偏置(bias),控制模型的基线偏移。
3. 参数的作用
w:斜率,决定预测价格随面积变化的速率。
例如:w 越大,面积增加时价格上升越快。
b:截距,表示面积为 0 时的基础价格
(二)参数 w,bw,b 的几何影响

例子 1:w=0, b=1.5
方程:f(x)=0⋅x+1.5(即 y=1.5)。
图形:一条水平直线,纵坐标恒为 1.5。
意义:
斜率 w=0 表示预测值 y 不随 x 变化。
截距 b=1.5 是直线与 y-轴的交点。
例子 2:w=0.5, b=0
方程:f(x)=0.5x。
图形:一条斜率为 0.5 的直线,通过原点。
意义:
斜率 w=0.5 表示 x 每增加 1 单位,y 增加 0.5 单位。
例子 3:w=0.5, b=1
方程:f(x)=0.5x+1。
图形:斜率为 0.5 的直线,与 y-轴交于 1。
意义:
斜率 w=0.5 同上。
截距 b=1 将直线上移 1 单位。
3. 关键结论
w的作用:决定直线的倾斜程度和方向。
w>0:直线向右上方倾斜。
w=0:水平直线(无相关性)。
w<0:直线向右下方倾斜。
b的作用:决定直线的起始位置(垂直偏移)。
三、理解代价函数:从数学公式到简化模型(以平方误差代价函数为例)
(一)代价函数公式与误差计算

1. 代价函数的目标
核心问题:如何衡量模型预测 fw,b(x)=wx+b 与真实值 y 之间的误差?
解决工具:代价函数 J(w,b) 量化所有训练样本的预测误差总和。
2. 平方误差代价函数的定义
数学公式:
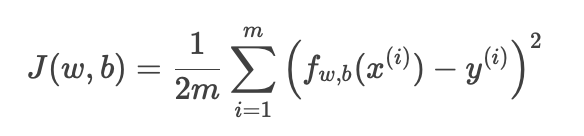
m:训练样本数量。
fw,b(x(i)):模型对第 i 个样本的预测值。
y(i):第 ii 个样本的真实值。
平方项:放大大误差,惩罚偏离更远的预测。
1/(2m):平均误差,且系数 1/2为后续求导方便(梯度下降时消去 2)。
3. 直观理解
图中标注:
公式中的 (fw,b(x(i))−y(i)) 是单个样本的预测误差(残差)。
Sum over all samples(求和符号 ∑):累加所有样本的误差。
目标:通过调整 w 和 b,最小化 J(w,b),使得预测线尽可能拟合数据点。
4. 关键点说明
为什么用平方误差?
对称性:正负误差同等对待。
可微性:便于优化算法(如梯度下降)找到最小值。

(二)平方误差代价函数与参数的关系
J(w,b) 的值随 w 和 b 的变化而变化




事实上,平方误差成本函数,形成碗形曲面(凸函数),存在唯一最小值。
三维:w,b,J(w,b)

但是在其他代价函数中,或许会根据参数w和b的位置,可能会以不同的局部最小值结束

