一、多元线性回归的含义

多元线性回归是一种统计方法，用于分析多个自变量（X）与一个因变量（Y）之间的线性关系。

通俗理解：
就像用多个“遥控器”（比如广告费、季节、产品价格）同时调节“电视音量”（比如销量），多元线性回归帮你算出每个遥控器对音量的影响有多大，并预测如果一起调整它们，音量会变成多少。

多元线性回归(图1).png

这幅图展示了一个多元线性回归的数据示例，具体内容如下：

表格部分：
- 前四列是自变量（特征）：房屋面积（平方英尺）、卧室数量、楼层数、房龄。
- 最后一列是因变量：房屋价格（单位：千美元）。
- 每行代表一个样本（共4条数据），例如第一行：2104平方英尺、5间卧室、1层、45年房龄，对应价格460千美元。
符号说明：
- x_j：第j个特征（如x1是面积，x2是卧室数）。
- n=4：特征总数（4个自变量）。
- x⁽ⁱ⁾：第i个样本的所有特征值（向量形式），例如x⁽²⁾=[1416,3,2,40]。（这里是行向量）
- x_j⁽ⁱ⁾：第i个样本的第j个特征值，例如x₃⁽²⁾=2（第2个样本的楼层数）。

二、多元线性回归模型公式

多元线性回归(图2).png

模型公式：
- 单变量线性回归的旧公式：f_w,b(x)=wx+b（仅一个特征x）。
- 扩展为多元线性回归的新公式：
  f_w,b(X)=w₁X₁+w₂X₂+w₃X₃+w₄X₄+b
  其中：
  - X₁到X₄：输入特征（如面积、卧室数等）。
  - w₁到w₄：每个特征的权重（系数）。
  - b：偏置项（截距）。
具体示例：

图中给出一个假设的权重值示例：
f_w,b(X)=0.1X₁+4kX₂+10X₃+(−2)X₄+80
对应特征：面积（X₁）、卧室数（X₂）、楼层数（X₃）、房龄（X₄）。
说明：
- 权重w₁=0.1表示面积每增加1平方英尺，价格增加0.1千美元。
- 权重w₄=−2表示房龄每增加1年，价格减少2千美元。
- b=80是基础价格（所有特征为0时的理论值）。

通用形式：
最下方公式为通用表达式：

f_w,b(x)=w₁x₁+w₂x₂+⋯+w_nx_n+b

适用于任意数量（nn个）的特征。

三、多元线性回归的向量化表示与参数解析

多元线性回归(图3).png

向量化模型公式：
- 多元线性回归的向量化表示：
  f_w⃗,b(x⃗)=w₁x₁+w₂x₂+⋯+w_nx_n+b
  也可以表示为向量点积形式：
  f_w⃗,b(x⃗)=w⃗⋅x⃗+b
  其中：
  - w⃗=[w₁,w_2,⋯ ,w_n] 是权重向量（模型参数）
  - x⃗=[x₁,x₂,⋯ ,x_n]是特征向量
  - b 是标量偏置项
关键说明：

公式明确区分了：
- 权重向量 w⃗（模型参数）
- 特征向量 x⃗（输入数据）
- 标量偏置 b
点积表示 w⃗⋅x⃗ 是权重和特征的线性组合

四、多元线性回归和线性回归区别

对比维度	线性回归 (Simple Linear Regression)	多元线性回归 (Multiple Linear Regression)
自变量数量	仅1个特征（X）	多个特征（X₁,X₂,…,X_n）
模型方程	f(x)=wx+b	f(x⃗)=w₁x₁+w₂x₂+⋯+b
参数意义	w：斜率，b：截距	w₁,w₂,…：各特征权重，b：全局截距
应用场景	单一因素对结果的影响（如温度对销量）	多因素共同影响（如面积、卧室数、房龄对房价）
几何解释	二维空间中的一条直线	高维空间中的超平面
计算复杂度	低（直接公式求解）	高（需矩阵运算或迭代优化）

线性回归是单变量的直线拟合，多元线性回归是多变量的超平面拟合，能更真实地反映复杂现实问题中多因素的共同作用。

五、多元线性回归梯度下降法

1. 多元线性回归梯度下降法简介

多元线性回归(图4).png

参数与模型
- 参数：权重 w₁,⋯ ,w_n 和偏置 b。
- 模型：线性函数 f_w,b(x⃗)=w₁x₁+⋯+w_nx_n+b，也可表示为向量点积形式 w⃗⋅x⃗+b。
代价函数
- 表示为 J(w⃗,b)，用于衡量模型预测值与真实值的误差。
梯度下降法
- 通过迭代更新参数来最小化代价函数：
- 重复执行直到收敛。

2. 梯度下降法在单特征（一元线性回归）和多特征（多元线性回归）中的具体实现步骤

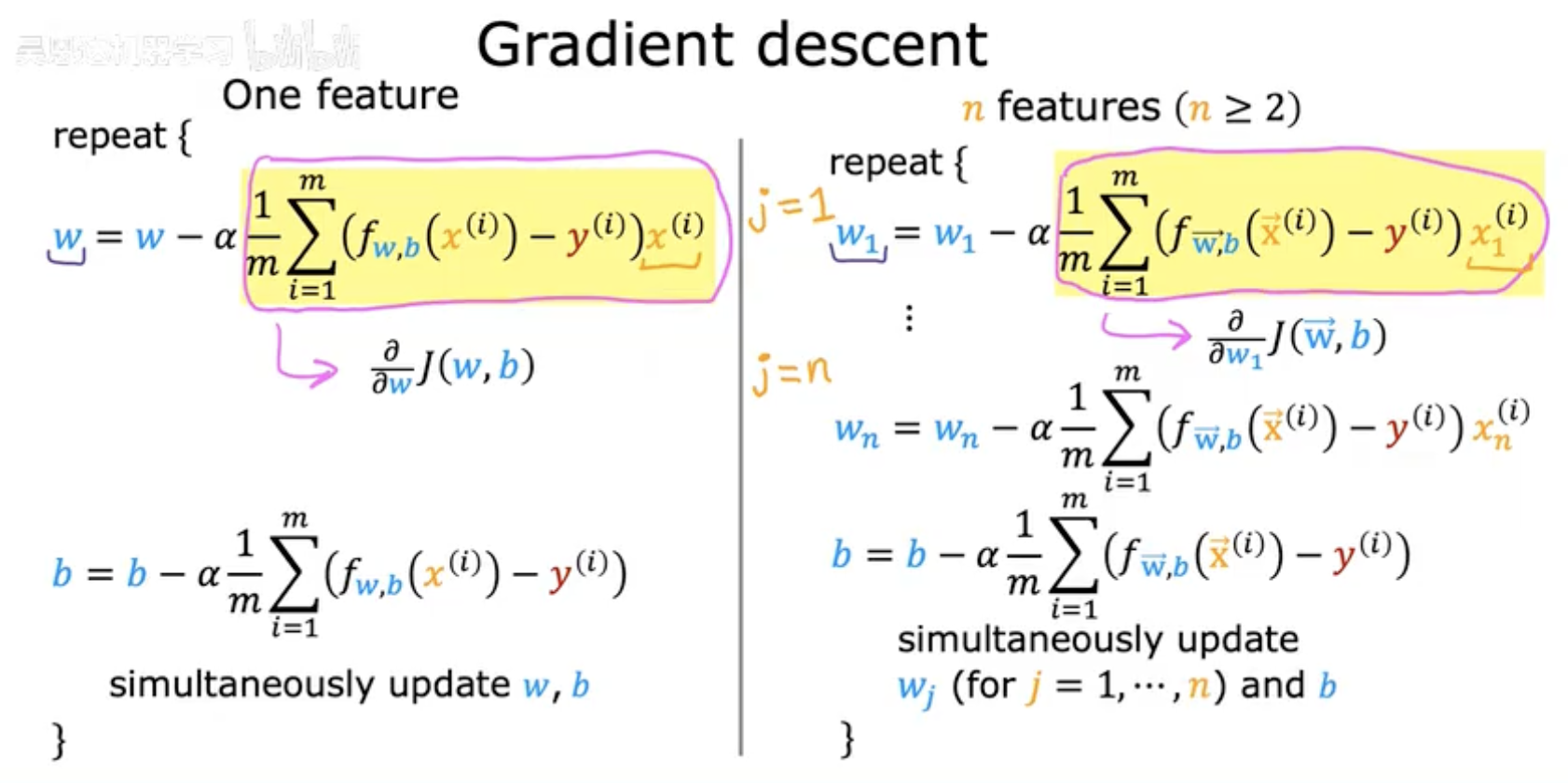
多元线性回归(图7).png

单特征（One Feature）

参数更新公式
- 权重 w 的更新：
  其中：
  - α 是学习率。
  - f_w,b(x⁽ⁱ⁾)=wx⁽ⁱ⁾+b 是模型预测值。
  - 求和部分是代价函数 J(w,b) 对 w 的偏导数（梯度）。
- 偏置 b 的更新：
  这是代价函数对 b 的偏导数。
同步更新（Simultaneous Update）
所有参数（w 和 b）需在同一轮迭代中更新，避免使用已更新的值计算其他参数。

多特征（n≥2 Features）

参数更新公式
对每个权重 wj（j=1 到 n）和偏置 b：
- 权重 wj 的更新：
  其中 x_j⁽ⁱ⁾ 是第 i 个样本的第 j 个特征值。
- 偏置 b 的更新（与单特征相同）：
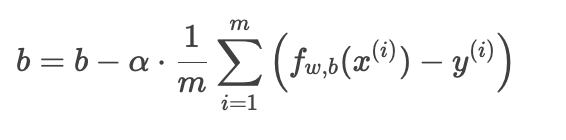
同步更新规则
所有 wj 和 b 需在同一轮迭代中更新，确保梯度下降的正确性。

六、正则方程

多元线性回归(图6).png

正规方程（Normal Equation）

功能
- 直接通过解析法（闭式解）计算最优参数 w⃗ 和 b，无需迭代。
- 仅适用于线性回归模型（不适用于其他机器学习算法如逻辑回归、神经网络等）。
数学形式
- 通过求解以下方程得到参数：
  θ=(X^TX)⁻¹X^Ty⃗
  其中：
  - θ 是包含 w⃗ 和 b 的参数向量。
  - X 是设计矩阵（每行一个样本，添加偏置列全为1）。
  - y⃗ 是目标值向量。

缺点

局限性
- 仅适用于线性回归，无法扩展至其他需要迭代优化的模型（如正则化模型、非线性模型）。
计算效率问题
- 当特征数量 n 很大（如 n>10,000）时，计算 (X^TX)⁻¹ 的复杂度高达 O(n3)，内存和速度会成为瓶颈。

关键结论

适用场景
- 正规方程可能在机器学习库的线性回归实现中使用，适合小规模数据集（特征少）。
推荐方法
- 梯度下降是更通用的方法，尤其适用于：
  - 大规模数据集（特征多或样本多）。
  - 需要扩展到其他算法（如逻辑回归、深度学习）。

对比总结

特性	正规方程	梯度下降
是否需要迭代	否，直接求解	是，需多次迭代更新参数
适用范围	仅线性回归	所有可微模型（通用性强）
计算复杂度	O(n3)O(n3)（特征多时慢）	O(mn)O(mn)（适合大规模数据）
内存需求	需存储 XTXXTX（可能巨大）	逐样本计算（内存友好）

尽管正规方程在某些场景下有效，梯度下降仍是更推荐的参数优化方法，因其通用性和可扩展性。

菜单

Multiple Linear Regression｜多元线性回归

分享