一、初始架构的回顾
在强化学习的早期阶段,深度Q网络(Deep Q-Network, DQN) 被提出,用于近似状态动作值函数 Q(s,a)。
在这种结构中,神经网络的输入并不仅仅是环境的状态,而是状态与动作拼接后的向量,输出为单一的 Q(s,a) 值。
架构结构说明

在图中,输入向量由状态 s 与动作 a 组成。
例如,状态 ss 包含位置、速度、角度、接触标志等信息,而动作 a 表示智能体在该状态下采取的操作,如“左推”、“右推”或“不动”。
整个向量:

输入网络后,依次经过两层隐藏层(每层64个神经元),最后输出一个标量 Q(s,a),表示在状态 s 下执行动作 a 的预期回报。
网络特点
输入层:12维(包含状态和动作)。
隐藏层:两个64单元的全连接层。
输出层:单一数值 Q(s,a)Q(s,a)。
网络对每个动作都需要独立输入并计算一次输出,即每执行一个动作都需重新计算 Q(s,a)。
局限性分析
计算冗余:
对每个动作都要单独输入状态与动作组合,导致重复计算。泛化能力差:
因为每次只学习单一动作的结果,模型难以同时捕获状态与动作间的全局关系。训练收敛慢:
每次迭代只优化一个 Q(s,a),样本效率较低。
二、改进后的架构设计
在改进后的深度Q网络架构中,核心思想是——不再将状态和动作拼接输入网络,而是仅输入状态 s,网络输出该状态下所有动作的 Q(s,a) 值。
这种方式极大提升了训练与推理效率,并在实际强化学习任务中表现出更稳定的性能。
架构改进思路
原始结构(第一节)中,每次只能计算一个动作的 Q(s,a)。
新的架构则让网络一次性输出所有动作对应的值:

从而能够在同一状态下立即比较所有动作的优劣,直接选择最优动作:
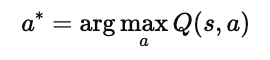
改进后网络结构

在图中,输入层仅包含 8维状态特征(例如位置 x,y、角度 θ、速度分量等),
网络结构如下:
输入层:8个状态输入。
隐藏层1:64个单元。
隐藏层2:64个单元。
输出层:4个单元,对应四个可能动作的 Q(s,a) 值。
输出层的每个节点都表示一个动作的价值,例如:

优势分析
计算效率显著提高
仅需一次前向传播即可得到所有动作的价值,减少了网络调用次数。结构更易扩展
可以轻松适应更多动作,只需调整输出层维度,无需改动输入部分。梯度传播更稳定
多动作并行计算增强了梯度平衡性,有助于加速收敛。直接与Bellman更新兼容
改进架构天然适合与Bellman方程结合,更新目标为:
实现高效、稳定的价值迭代。
三、改进结构的核心变化
从前两张图可以直观看到,改进后的神经网络架构在输入与输出层的设计上进行了关键性的变化,
这种变化极大地提升了强化学习算法在连续状态环境中的运算效率与稳定性。
1. 输入层的变化:从状态+动作到仅状态
在旧架构中(第一张图),输入是“状态 + 动作”拼接向量。
每次只能输入一种动作组合,因此要计算所有动作的 Q 值时,
需要对每个动作都单独执行一次前向传播。
而在新的架构中(第二张图),输入层仅保留状态向量 ss,
网络会自动输出所有动作的 Q 值。
这意味着一次前向传播即可获得:

这样的设计彻底消除了冗余输入,提升了计算效率。
2. 输出层的变化:从单输出到多输出
旧网络的输出层只有一个神经元,对应单个动作的 Q(s,a)。
而新网络的输出层包含四个神经元,分别对应四种可能动作的 Q 值。
这种“一对多”的结构使得智能体可以在同一状态下,
直接比较不同动作的价值,而无需重复运算。
这不仅提升了推理速度,还使得训练中梯度更新更平衡、收敛更稳定。
3. 计算效率与性能提升
通过这种设计改进,神经网络能够同时理解状态空间和动作空间之间的全局关系,
实现更高效的策略学习与价值估计。
四、总结与启示
通过对比两种网络结构,我们可以看到:
算法的优化并不一定需要更复杂的公式或更大的模型,
有时,仅仅是对网络输入输出结构的重新设计,
就能带来显著的性能提升与稳定性改善。
从“逐动作计算”到“一次性输出”
原始的深度Q网络(DQN)结构虽然直观,但效率低下。
它要求智能体在每个状态下,分别为每个动作计算一次 Q 值,
这种方式在动作数量较多时,会让计算量急剧上升。
改进后的架构打破了这种局限:
输入只需状态 s;
输出一次性包含所有动作的 Q 值;
训练与推理效率显著提升。
这不仅节省了计算资源,也让算法更易扩展到高维连续场景。
算法稳定性与泛化能力
由于网络在同一状态下同时预测多个动作,
模型能够在训练中学习到状态与动作间的全局模式,
避免了原架构中“局部更新、全局割裂”的问题。
这种全局学习能力使得网络收敛更平滑、
对噪声或随机性的适应性更强。
启示与展望
这种架构优化的思路,启发我们在后续算法设计中:
不仅关注算法本身的公式优化(如目标函数、损失函数),
还要重视网络结构的合理性,
特别是在强化学习中,结构设计往往决定了信息流动的效率。
未来还可以进一步扩展这种思路,
例如结合 Double Q-Network、Dueling Network 或 卷积特征提取层(CNN),
在保证高效的同时进一步提升稳定性与表达能力。
