一、引言:为什么需要贝尔曼方程
在强化学习中,我们希望智能体(agent)能够在一个环境(environment)中不断行动,以最大化它获得的累积回报(return)。
但问题在于,未来的回报是未知的 —— 只有在执行了一系列动作之后,才能真正看到结果。
那么,我们如何在当前时刻就知道一个动作是否“好”呢?
这就需要一种能够递归地表示未来回报的方式,
让智能体能够“往前看” —— 通过当前奖励与对未来的估计结合起来,形成对整体回报的合理预测。

1️⃣ 从回报到价值的思考
假设我们在一个环境中有若干状态(states),
每个状态执行一个动作(action)后会获得即时奖励(reward)并转移到下一个状态。
于是我们定义了:
状态值函数 V(s):在状态 s 下遵循某个策略后,能获得的期望回报。
状态-动作值函数 Q(s,a):在状态 s 下执行动作 a 后,长期能获得的期望回报。
但这些值函数之间并不是孤立的,它们之间存在一种递推关系:
当前的价值取决于当前奖励 + 下一状态的价值。
2️⃣ 贝尔曼方程的出现
为了刻画这种递推关系,我们引入了一个非常重要的思想:
“当前的价值 = 当前奖励 + 折扣后的未来价值”
这便是强化学习的基石 —— 贝尔曼方程(Bellman Equation)。
它把复杂的长期最优决策问题,拆解成一系列局部的最优决策问题,
从而让算法能够通过动态规划(Dynamic Programming)或迭代学习(如 Q-learning)逐步逼近最优策略。
二、Q 函数回顾与引入
在上一节中,我们提到强化学习的核心是评估“当前行动能带来多大长期收益”。
这一思想的数学表达,正是 Q 函数(State–Action Value Function)。
1️⃣ 什么是 Q 函数?
Q 函数通常记作:
Q(s,a)
它的含义是:
从状态 s 开始,执行动作 a,然后按照某个最优策略继续行动,最终能获得的期望回报。
换句话说,Q 值不仅考虑了当前动作的即时奖励,
还反映了这个动作对未来回报的影响。
因此,Q 函数是连接当前决策与长期目标之间的桥梁。
它回答的问题是:“在这个状态下做这个动作值不值?”
2️⃣ 图像理解:状态、动作与回报的联系
你上传的第一张图很好地展示了这一逻辑:
在图中,网格代表不同的 状态(state),
箭头代表可能的 动作(action),
每个状态上方的数值是它的 即时奖励(reward)。
蓝色的手写部分则定义了 Q 值计算方式:
当你在某个状态采取一个动作后,你会立刻得到奖励 R(s)。
接着进入下一个状态 s′,在那里你继续采取最优动作 a′。
最终,总回报就是这两个部分的叠加。
也就是说:
Q(s,a) 记录了从某个状态出发、执行某个动作后的一条“未来收益轨迹”。
3️⃣ 为什么要引入 Q 函数
在许多强化学习场景(比如迷宫导航、机器人决策、围棋),
智能体需要同时考虑“我现在在哪儿(state)”和“我打算做什么(action)”。
单独使用状态值函数 V(s) 无法区分不同动作的好坏,
而 Q 函数 Q(s,a) 能明确告诉我们:
“在这个状态下,选哪个动作能获得最高的长期收益。”
因此,它为强化学习的“行动选择”提供了量化依据,
而下一节的 贝尔曼方程,正是对 Q(s,a) 的递归定义。
三、贝尔曼方程的数学形式
Q 函数定义了“在状态 ss 下执行动作 aa”的长期回报,
而 贝尔曼方程(Bellman Equation) 则揭示了这些 Q 值之间的递推关系。
1️⃣ 公式定义
贝尔曼方程的核心公式是:
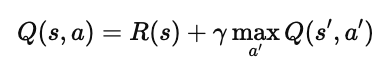
其中:
s:当前状态(current state)
a:当前动作(current action)
s′:执行动作 a 后到达的下一个状态(next state)
a′:在下一个状态下可能采取的动作
R(s):当前状态的即时奖励(reward of current state)
γ:折扣因子(discount factor),用于平衡“现在的奖励”和“未来的奖励”
2️⃣ 含义解释
这个公式可以这样理解:
当前的 Q 值 = 立即获得的奖励 + 折扣后的未来最优回报。
也就是说,智能体在每个状态中执行一个动作,
它不仅考虑眼前的收获(R(s)),
还会思考“下一步如果继续表现得最优,能得到多少”。
这正是强化学习的核心思想:在短期与长期之间权衡决策。
3️⃣ 折扣因子 γ 的意义
γ 的取值范围是 0≤γ≤1:
当 γ 越大(如 0.99),智能体越关注长期收益;
当 γ 越小(如 0.5),智能体越重视即时奖励。
举个直观的比喻:
γ 决定了智能体的“远见”程度。
γ 大,代表“长远主义”;γ 小,代表“短视行为”。
四、从实例看贝尔曼方程的意义
为了让贝尔曼方程不再只是抽象的公式,我们通过一个具体的 Q 值计算例子来理解它的运作过程。
1️⃣ 示例环境说明
我们依旧使用“火星探测车(Mars Rover)”的简单一维环境:
共有 6 个状态(编号 1–6);
终止状态(Terminal states)是 状态 1 和 状态 6;
它们的奖励分别是:
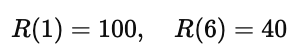
其他状态的奖励均为 0;
折扣因子(Discount Factor)取 γ=0.5。
2️⃣ 计算 Q 值的过程

我们以 Q(2,→) 为例来理解:
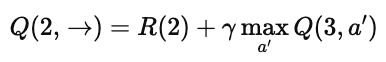
由于 R(2)=0,所以关键是看 状态 3 的最优行为:
图中标出了 Q(3,→)=25。
于是:
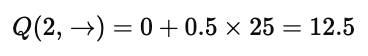
这表明——
在状态 2 选择“向右”行动,其长期期望回报是 12.5。
再看另一个例子:Q(4,←)
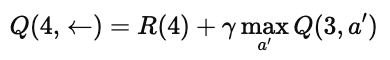
同样,R(4)=0,而状态 3 的最优 Q 值为 25:
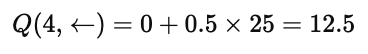
这说明——
尽管状态 4 和状态 2 位置不同,它们的最优行为所带来的期望回报是相同的。
3️⃣ 图像中的逻辑
在图中可以看到:
上半部分的网格表示奖励(reward)与返回值(return);
蓝色圆圈标出了关键状态;
右侧的蓝色公式对应刚才的两个 Q 值计算;
最终结果都与折扣因子 γ 和下一个状态的最优值相联系。
这实际上体现了 贝尔曼方程的递归本质:
每个状态的价值由当前奖励 + 下一个状态的价值组成。
4️⃣ 递归展开的直观理解

当继续展开时:
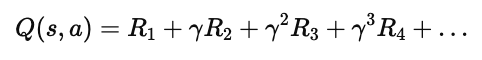
即:
当前 Q 值代表了从当前状态出发、未来所有奖励的折扣和。
它让我们能够用一步的计算,预测长期的整体回报。
5️⃣ 计算实例验证
这张图则展示了用具体数值代入公式的验证过程:
Q(4,←)=0+(0.5)[0+(0.5)0+(0.5)2100]Q(4,←)=0+(0.5)[0+(0.5)0+(0.5)2100]
化简得到:
Q(4,←)=12.5Q(4,←)=12.5
这正与前面通过递推计算得到的结果一致,
验证了贝尔曼方程的正确性与一致性。
五、贝尔曼方程的意义
贝尔曼方程是强化学习中最核心的思想之一。
它告诉我们:
一个状态或动作的价值,可以分解为当前奖励与未来价值的加权和。
这种递推形式让智能体能够一步步学习最优策略,
不需要提前知道整个未来,只要不断更新自己的估计即可。
几乎所有强化学习算法(例如 Q-Learning、DQN)都以它为基础,
通过反复逼近贝尔曼方程来改进策略。
简单来说:
贝尔曼方程让“面向未来的决策”成为可能,
让强化学习从直觉走向可计算。
