一、状态-动作值函数定义
在强化学习中,智能体在与环境交互的过程中,需要根据当前状态做出一个动作(action),并获得一个奖励(reward)。
然而,智能体并不仅仅关心立即获得的奖励,而是希望在长期内获得尽可能高的回报(return)。
为了实现这一目标,我们需要衡量在不同状态下采取不同动作的“好坏”。
于是,状态-动作值函数(State-Action Value Function),也称为 Q 函数(Q-function),应运而生。
Q 函数的核心思想是:
Q(s, a) 表示如果智能体在状态 s 下采取动作 a,并且此后始终按照最优策略行事,所能获得的期望回报。
它是强化学习的一个核心函数,构建了状态(state)与动作(action)之间的价值桥梁。
换句话说,Q 函数能告诉智能体:“在当前状态下执行哪个动作,未来能带来最大的长期收益。”
二、Q 函数的数学定义
我们知道,强化学习的目标是最大化长期累积回报(Return),而 Q 函数正是对这种长期回报的数学化刻画。
Q 函数(State–Action Value Function)的定义如下:
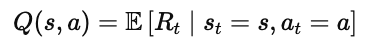
这里:
st:表示在时间步 tt 时刻的状态;
at:表示在状态 stst 下采取的动作;
Rt:表示从时间步 tt 开始的累计回报(Return)。
更具体地,累计回报 RtRt 可以写作:
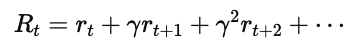
其中:
rt 是即时奖励(reward);
γ∈[0,1] 是折扣因子(discount factor),用于平衡短期和长期收益。
与状态值函数的区别
我们之前介绍过状态值函数 V(s),它表示“在状态 s 下,按照策略 π 行动后,所能获得的期望回报”。
两者的区别在于:
换句话说,V 函数回答“我在这里的价值是多少”,而 Q 函数回答“我在这里做某件事的价值是多少”。
三、计算 Q 值的示例

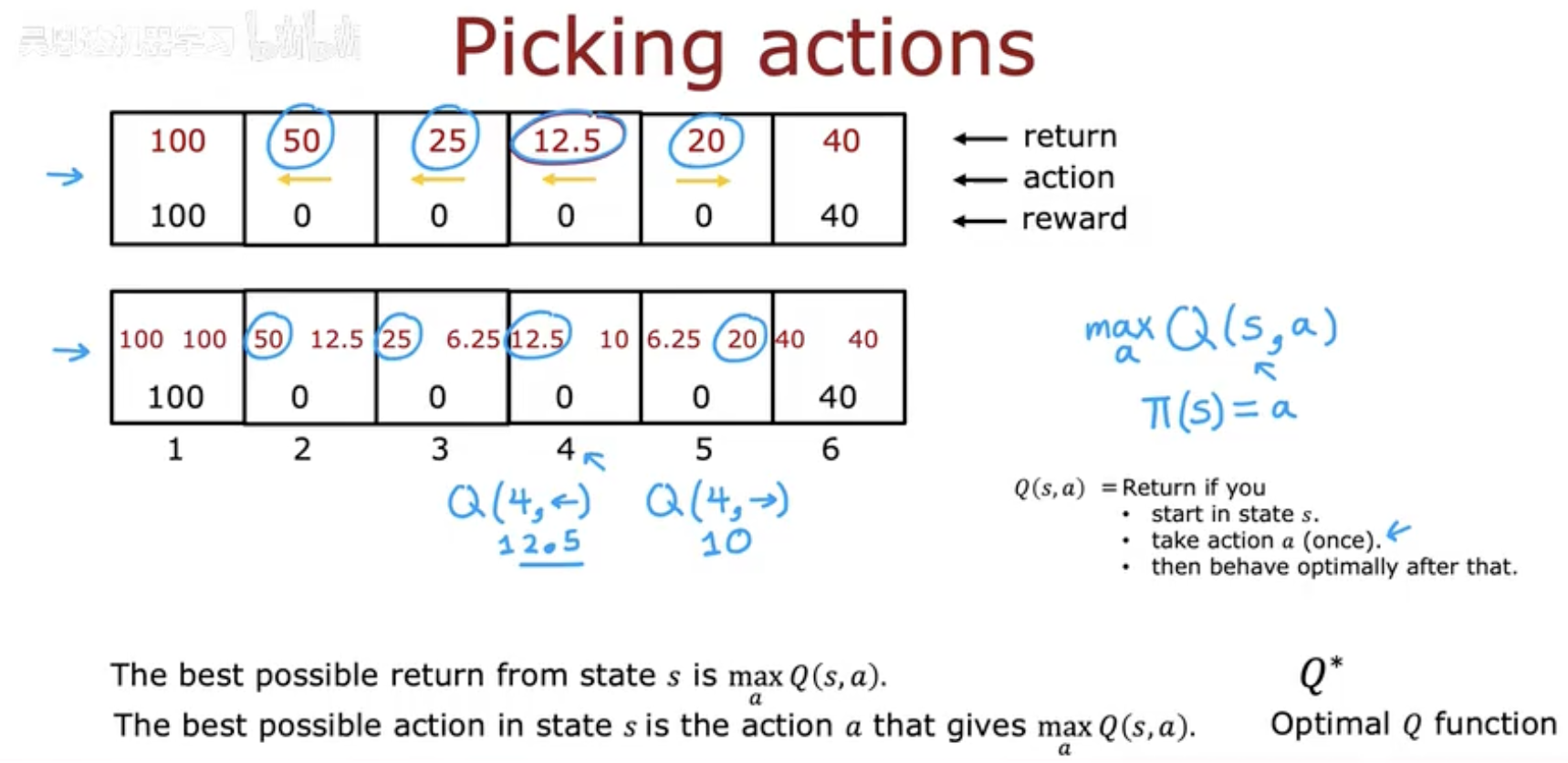
这张图展示了一个简化的环境:智能体(例如火星车)在一条直线上移动。每个方格代表一个状态(state),智能体可以**向左(←)或向右(→)**移动。终止状态分别有奖励值(左边 100,右边 40),其余状态奖励为 0。
Q 函数的定义回顾
我们定义:
Q(s,a)=Return if you start in state s, take action a once, then behave optimally thereafter.Q(s,a)=Return if you start in state s, take action a once, then behave optimally thereafter.
也就是说:
在状态 s 下先执行一次动作 a,然后再按照最优策略行事。Q 值衡量的就是在此策略下最终能得到的期望回报。
示例讲解
我们以折扣因子 γ=0.5 为例,计算几个关键的 Q 值:
1️⃣ 在状态 2 向右移动:
Q(2,→)=0+(0.5)×0+(0.5)2×0+(0.5)3×100=12.5
也就是说,如果在状态 2 选择向右移动,经过若干步后能获得约 12.5 的折扣回报。
2️⃣ 在状态 2 向左移动:
Q(2,←)=0+(0.5)×100=50
显然,这一动作更好,因为离高奖励(100)更近。
3️⃣ 在状态 4 向左移动:
Q(4,←)=0+(0.5)×0+(0.5)2×0+(0.5)3×100=12.5
同样,也能计算出 Q 值约为 12.5。
通过这些计算,我们可以发现:
Q 值不仅与状态 s 有关,还强烈依赖于动作 a。
在相同状态下,不同动作的回报差距可能非常大。
这也正是强化学习要解决的问题——如何在每个状态下选择最优动作。
四、根据 Q 值选择最优动作
既然我们已经计算出了每个状态下不同动作对应的 Q 值,那么问题就变成了:
智能体该如何根据这些 Q 值来选择下一步动作?
这就是策略改进(Policy Improvement)的核心思想。
1️⃣ 动作选择原则
我们希望智能体在每个状态 s 下选择能带来最大长期回报的动作,也就是:
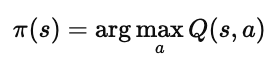
这意味着:
对于每个状态 s,
我们计算所有可能动作的 Q(s,a),
然后选择 Q 值最大的那个动作。
在状态 4 中,
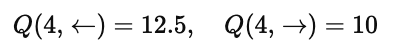
因此:
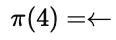
也就是说,最优策略会选择“向左移动”。
2️⃣ 最优 Q 函数 Q∗
我们定义:
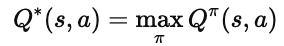
也就是在所有可能的策略 π 中,某个状态–动作组合能够达到的最高期望回报。
换句话说:
Q(s,a)是在某个策略下的值;
Q∗(s,a) 是最优策略下的值。
当我们得到了 Q∗ 后,就可以轻松确定最优策略:
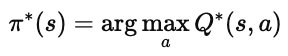
3️⃣ 小结
Q 函数:衡量状态–动作组合的长期回报。
最优 Q 函数 Q∗:描述在最优策略下每个动作的最终潜力。
最优策略 π∗:选择在每个状态中使 Q 值最大的动作。
换句话说,强化学习的目标可以概括为:
找到能最大化 Q(s,a) 的策略 π。
