一、随机环境的定义

在强化学习中，环境（Environment） 指的是智能体所处的世界。智能体通过感知环境状态（state）并执行动作（action），从而获得奖励（reward）并转移到下一个状态。

在前面的讨论中，我们默认环境是确定性的（Deterministic） ——
也就是说，只要智能体采取同样的动作，结果总是一样的。

然而，在很多现实任务中，事情并非如此。
比如机器人在移动过程中，可能因为地面摩擦或风向变化而偏离路线；
或者在金融交易中，同一决策在不同时间可能带来不同收益。

这类具有随机性（Stochasticity） 的环境就被称为——

🎲 随机环境（Stochastic Environment）

在这种环境下，动作的结果不是固定的，而是以一定概率分布（Probability Distribution） 出现。
这意味着：

• 执行相同的动作，可能到达不同的状态；

• 获得的奖励也可能不同；

• 强化学习的目标不再是追求“确定的最大值”，而是最大化期望收益（Expected Return）。

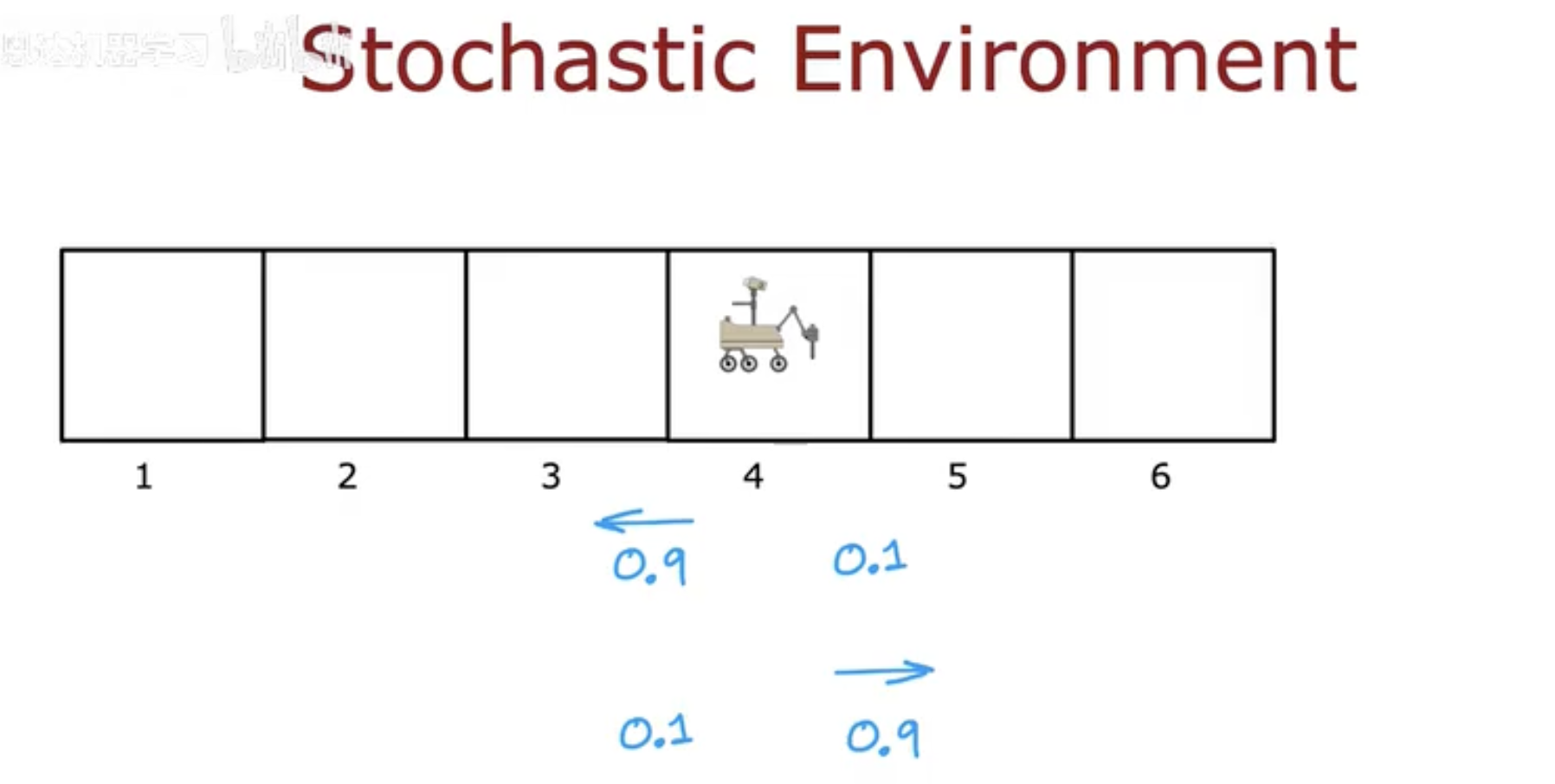
图中展示了一个简化的场景：
一个机器人处在格子世界的第4个位置，
它有两个可能的动作——向左 或 向右。

但即使选择“向左”：

• 有 90% 的概率真的向左移动；

• 仍有 10% 的概率会出错，向右走。

这正体现了随机性：
动作的结果并不总是完全可控，而是由环境的不确定性决定。

二、行为与结果的不确定性

在随机环境中，智能体的动作（Action） 不再唯一决定它的下一个状态（Next State）。
即使执行了同样的动作，由于环境具有随机性，智能体也可能到达不同的位置。

在这幅图中，机器人站在格子 4 上：

• 如果它选择 向左移动（←），

  • 以 0.9 的概率 它确实会向左移动到格子 3；

  • 但仍有 0.1 的概率，它会“走错方向”，反而移动到格子 5。

• 同样地，如果它选择 向右移动（→），

  • 以 0.9 的概率 它会到达格子 5；

  • 但也有 0.1 的概率 反而会往左回到格子 3。

换句话说，

行动的执行结果，不再是确定的状态转移，而是一个概率分布 P(s′|s,a)。

这时我们不再说：

“执行动作 a 后一定到达状态 s′”，
而应该说：
“执行动作 a 后，有一定概率到达状态 s′”。

这正是随机环境的本质区别。

启示

在这种环境中，强化学习的难度显著提升：

• 智能体无法通过一次行动就明确评估动作的好坏；

• 它需要多次交互，通过统计来估计动作的平均回报。

因此，强化学习的目标变成了：

学习一套策略，使得在长期的平均意义下，获得的期望回报（Expected Return） 最大。

三、期望回报（Expected Return）

当环境中存在随机性时，智能体的行动结果和获得的奖励就会带有不确定性。
这时，我们不再追求某一次行动的具体收益，而是要关注它的平均收益——
也就是行动在长期多次执行后，能带来的期望值（Expected Value）。

这就是期望回报（Expected Return）的核心思想。

1. 概念公式

在确定性环境中，我们定义回报（Return）为：

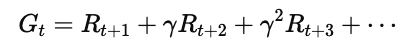
而在随机环境（Stochastic Environment）中，
每次执行动作后获得的 RtRt​ 并不是固定的，
于是我们取它的期望：

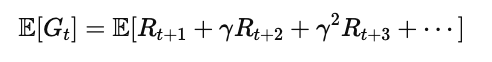
其中：

• E[⋅] 表示对随机性的平均；

• γ 是折扣因子（Discount Factor），控制未来奖励的重要性；

• 目标是最大化这一 期望总回报。

2. 图片讲解：Expected Return 示例

图中展示了一个机器人从右向左移动的格子世界。
每个格子可能带来不同的奖励（Reward）：

• 状态 1：奖励 100

• 状态 6：奖励 40

• 其他状态：奖励为 0

机器人每次移动都会遇到不同结果，可能走对也可能走错。
于是我们记录下多次执行的结果，求它们的平均值。

在图的下方：

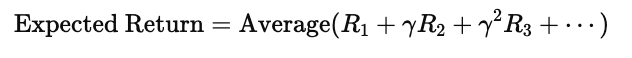
它表示：

多次行动后，所有可能的奖励序列的平均回报。

小结

在确定性环境中，“回报”是一个确定值；
而在随机环境中，“回报”是一个分布。
强化学习智能体要学会估计这一分布的平均值，也就是——

期望回报（Expected Return）。

四、期望贝尔曼方程（Expected Bellman Equation）

在前面我们学习过确定性环境下的贝尔曼方程：

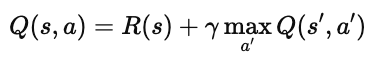
它表示——
在状态 s 执行动作 a 所得到的回报，等于：

• 当前立即获得的奖励 R(s)，加上

• 折扣后的下一状态 s′ 的最大价值。

但在随机环境（Stochastic Environment）中，
动作 a 执行后可能导致多个不同的结果，
因此 s′ 不再唯一。
于是我们必须对所有可能的结果求期望。

1. 公式形式

于是，贝尔曼方程被改写为：

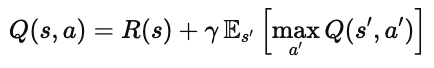
也可以写成带转移概率的形式：

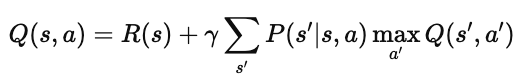
其中：

• P(s′∣s,a)：表示从状态 ss 采取动作 aa 后，转移到 s′s′ 的概率；

• E_s′：表示对所有可能后续状态的期望；

• max⁡_a′Q(s′,a′)：表示在下一状态下采取最优动作的回报。

2. 图片讲解：Expected Return 与 Bellman 方程的结合

图中展示了强化学习的最终目标：

学习一个策略 π(s)=a，
让我们在每个状态下选择最优动作，从而最大化期望回报（Expected Return）。

结合随机环境的特性，Bellman 方程被改写为：

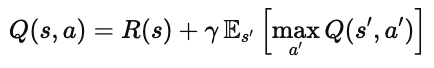
它体现了强化学习的三个核心要素：

1. 即时奖励 R(s)：当前获得的收益；

2. 未来期望回报 E_s′[⋅]：考虑未来可能状态的平均收益；

3. 最优行为选择 max⁡_a′：智能体始终选择让未来最优的行动。

举例理解

假设机器人从状态 3 选择动作 “→”：

• 它有 90% 的概率到达状态 4，

• 也有 10% 的概率因为环境波动而回到状态 2。

那么该动作的期望价值就是：

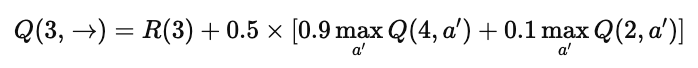
小结

在随机环境中，
贝尔曼方程不仅要考虑最优行为，还要加上概率期望项，
这让智能体学会应对环境不确定性带来的挑战。

✅ 最终目标：
学习能在随机世界中表现最优的策略 π^∗(s)。

五、总结：在随机世界中学习决策

在确定性环境中，智能体可以完全预测自己的行动结果；
而在随机环境（Stochastic Environment）中，
即使做出相同的选择，也可能因为环境的变化而产生不同的后果。

因此，强化学习要学会的不再是“哪一步一定最优”，
而是“哪一步在平均意义下期望最优”。

🎯 关键思想回顾

1. 动作的结果是随机的
   相同动作可能通往不同状态，用概率 P(s′∣s,a)P(s′∣s,a) 来描述。

2. 智能体的目标是最大化期望回报
   它不追求每次都获得最大收益，而是让长期的平均收益最高。

3. 贝尔曼方程引入期望项
   在随机环境中，状态转移需要考虑所有可能结果的加权平均：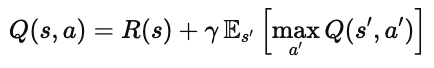

   

💡 启示

随机性让强化学习更贴近真实世界：
无论是自动驾驶、推荐系统还是机器人控制，
都无法保证每个动作的结果完全一致。

贝尔曼方程的“期望形式”让智能体能够在这种不确定性中学会稳定的决策策略。

✅ 简而言之：
随机性不是障碍，而是智能体学习“概率意义上的智慧”的开始。