一、分类(Classification)的基本概念
1.1 有监督学习与无监督学习
在进入分类任务之前,需要先区分两个非常基础的概念:有监督学习和无监督学习。
有监督学习中,每一条训练样本都带有明确的类别标签(label),模型通过学习这些已知标签的数据,去预测新样本所属的类别。分类(Classification)就是有监督学习中最典型的任务之一,比如垃圾邮件识别、人脸识别、疾病诊断等。
无监督学习则不同,训练数据中没有类别标签,算法只能依靠数据本身的结构和分布规律,去发现潜在的模式或分组结构。常见的无监督任务就是聚类(Clustering)。
简单来说:
有监督学习:有答案,模型学习如何找答案。
无监督学习:没有答案,模型自己发现规律。

1.2 分类的定义
在数据挖掘和机器学习中,分类(Classification)指的是:
在给定一个带有类别标签的训练数据集时,学习一个模型,该模型可以将新的样本映射到已知的类别标签上。
通常,一个样本可以表示为一个二元组:
(x,y)
其中:
x:样本的属性集合(attributes / features),也可以称为特征向量。
y:样本的类别标签(class label)。
在不同领域中,这些变量也有不同称呼:
x:attribute、predictor、independent variable、input
y:class、response、dependent variable、output
分类任务的核心目标,就是学习一个映射关系:
f(x)→y
也就是从输入属性集合到类别标签的映射。

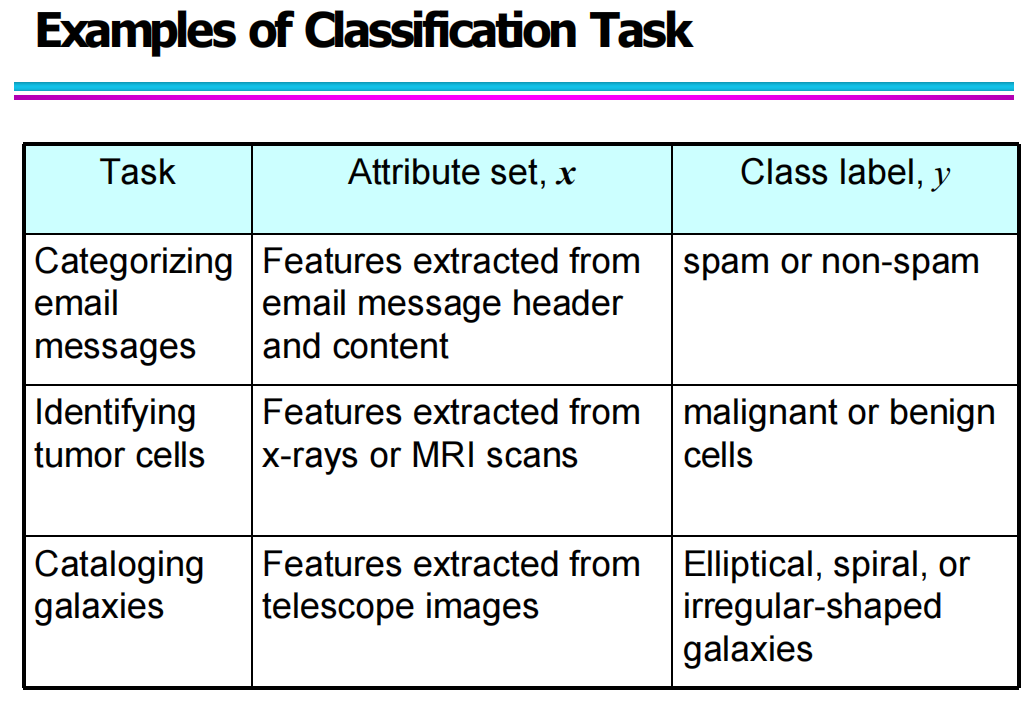
1.3 常见的分类任务示例
为了让分类更容易理解,我们可以通过实际任务来说明它的应用场景。典型的分类任务包括:
垃圾邮件分类(Spam Filtering)
特征:从邮件标题和内容中提取的关键词、频率等
类别:Spam 或 Non-Spam
肿瘤诊断(Tumor Identification)
特征:从医学影像(如 X-ray、MRI)中提取的形态特征
类别:Malignant(恶性)或 Benign(良性)
星系分类(Galaxy Classification)
特征:从天文图像中提取的结构、亮度等信息
类别:椭圆星系、螺旋星系、不规则星系等
这些任务的共同点在于:
输入是特征集合
输出是有限个类别标签之一
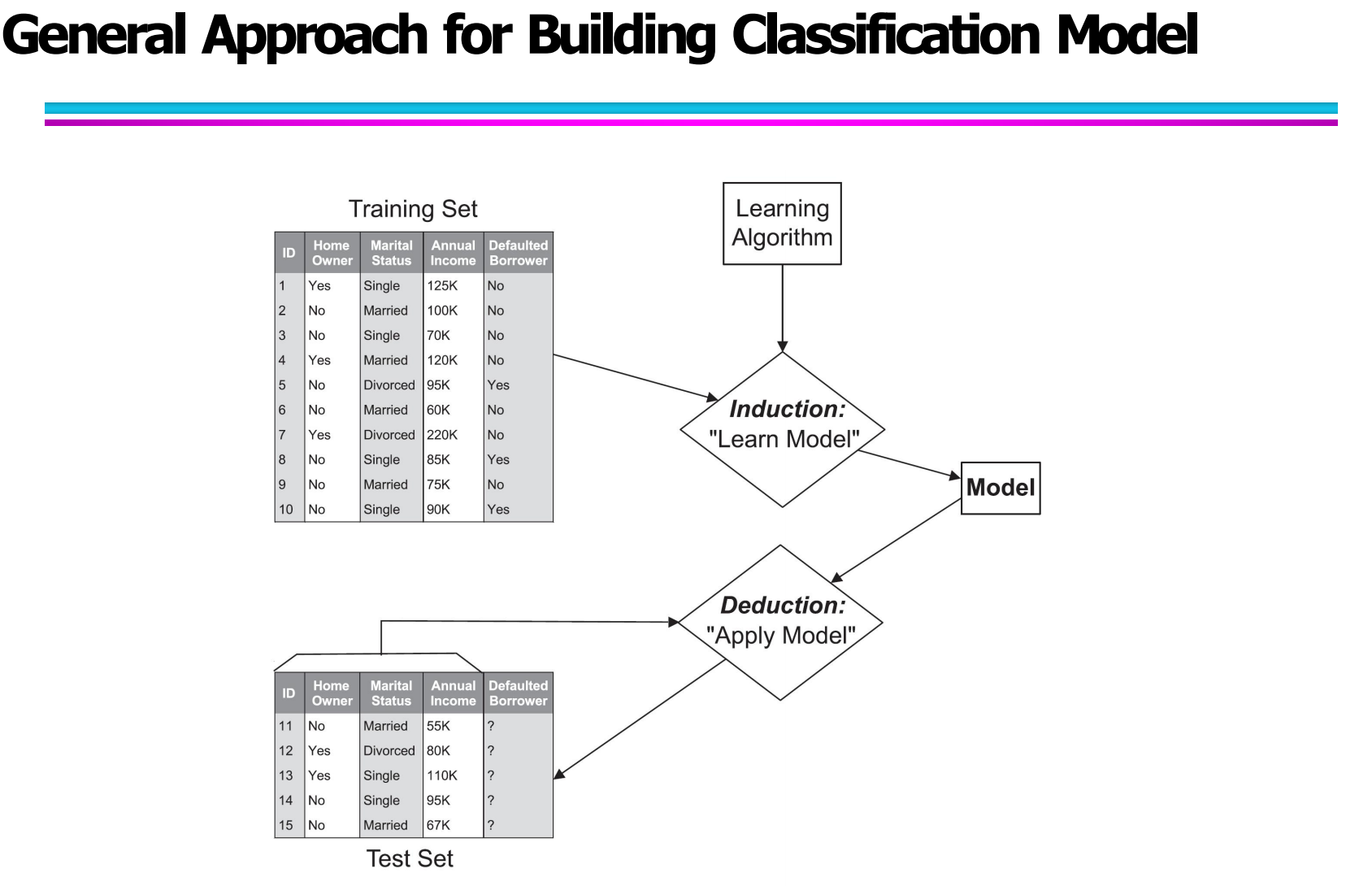
二、建立分类模型的一般方法(General Approach for Building Classification Model)
2.1 分类模型构建的整体框架(Overall Framework of Classification Model Building)
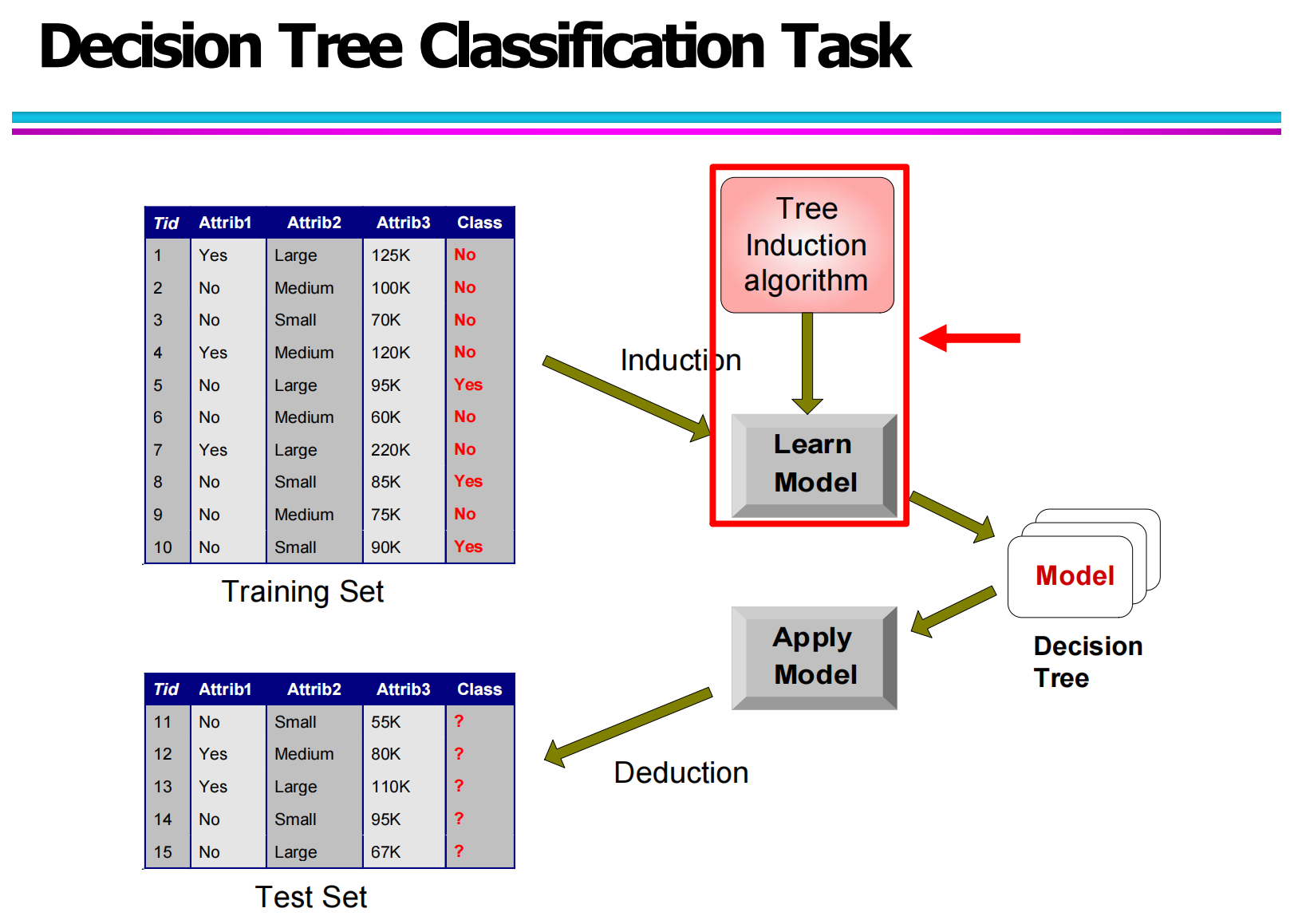
在分类问题中,模型构建过程本质上是一个从“已知样本”到“未知样本预测”的过程。这个过程通常分为两个核心阶段:归纳(Induction) 与 演绎(Deduction)。
在归纳阶段,输入的是一个带有类别标签的训练集。训练集中的每一条数据,都由多个属性(如收入、婚姻状况、是否有房产等)和一个已知的类别标签组成。学习算法的任务是从这些样本中发现数据与类别之间的潜在规律,并通过这些规律构建出一个分类模型。
而在演绎阶段,训练好的模型会被应用到新的数据上。这些新数据的属性结构与训练集相同,但其类别标签是未知的。模型会根据之前学到的分类规则,为这些新样本预测对应的类别。例如,在贷款违约预测问题中,模型会判断一个新客户是否可能成为违约用户。
整个过程可以概括为:
Training Set → Learning Algorithm(Induction)→ Model → Deduction → Classification Result
2.2 分类模型构建的关键步骤(一)(Key Steps in Building a Classification Model - Part I)
在理解了整体框架之后,进一步来看分类模型构建中的几个关键步骤。本小节主要涵盖前三个核心阶段:数据收集、数据预处理和模型选择。

2.2.1 数据收集(Data Collection)
数据收集是整个分类过程的第一步,也是后续分析的基础。这里收集的数据必须包含输入属性和对应的类别标签,也就是所谓的“有标签训练数据”。
举例来说,如果我们要构建一个垃圾邮件分类模型,那么数据集应该包含大量邮件样本,每封邮件不仅要有内容特征,还必须标注其类别(例如:垃圾邮件或正常邮件)。数据的数据量、质量和代表性,对后续模型性能有着非常直接的影响。
2.2.2 数据预处理(Data Preprocessing)
原始数据往往是“脏”的,不能直接用于模型训练,因此在正式训练之前,必须对数据进行预处理。常见的预处理步骤包括:
处理缺失值(如用均值、中位数或众数填充)。
处理异常值,去除明显偏离正常范围的数据。
对属性进行变换(如标准化、归一化)。
对连续属性进行离散化(如果算法需要)。
这些操作的目的,是让数据更加干净、规整,从而提高模型的稳定性和泛化能力。
2.2.3 模型选择(Model Selection)
数据准备好了之后,就需要选择合适的分类算法来构建模型。不同算法适用于不同问题场景,常见的分类算法包括:
决策树(Decision Tree)
支持向量机(Support Vector Machine, SVM)
k近邻算法(K-Nearest Neighbors, KNN)
例如,对于结构化数据且希望模型具有较强可解释性的场景,决策树往往是一个不错的选择;而对于高维数据问题,支持向量机通常表现较好。
模型选择的过程通常是一个不断比较和试验的过程,需要通过实验验证不同模型在数据集上的表现,最终选择效果更优的模型。
2.3 分类模型构建的关键步骤(二)(Key Steps in Building a Classification Model - Part II)
在完成模型选择之后,接下来要进行模型训练、模型评估以及模型部署,这也是非常关键的三个阶段。

2.3.1 模型训练(Training the Model)
模型训练阶段,是利用训练数据让算法自动学习数据中的模式。通过不断调整模型参数,使得模型在训练集上的分类误差不断减小。
在这个过程中,模型会逐渐掌握输入特征与类别之间的映射关系。例如,在银行贷款数据中,模型可能会学习到:收入较低且没有房产的用户,违约风险相对更高。
2.3.2 模型评估(Model Evaluation)
一个模型在训练集上表现好,并不代表它在新数据上也表现好。因此,我们需要使用验证集或测试集,对模型进行评估,以衡量模型的泛化能力。
常见的评估方式包括:
划分训练集 / 测试集
使用交叉验证(Cross-Validation)
通过评估,可以判断模型是否存在过拟合或欠拟合问题,并进一步调整模型结构或参数。
2.3.3 模型部署(Model Deployment)
当模型经过训练和评估后,如果其效果满足实际需求,就可以部署到真实系统中,对新的数据进行自动分类。
例如,信用评估系统可以使用分类模型来判断新用户的信用风险;垃圾邮件系统则可以实时对邮件进行自动分类。这一步是模型从“理论研究”走向“实际应用”的关键环节。
三、分类技术(Classification Techniques)
3.1 基础分类器(Base Classifiers)
在分类任务中,基础分类器是最常见、也是最基本的一类模型,它们直接利用训练数据构建分类规则,不依赖多个模型的组合。
常见的基础分类器包括:
决策树方法(Decision Tree Based Methods)
基于规则的方法(Rule-based Methods)
最近邻方法(Nearest-neighbor)
朴素贝叶斯与贝叶斯网络(Naïve Bayes & Bayesian Belief Networks)
支持向量机(Support Vector Machines, SVM)
神经网络与深度神经网络(Neural Networks & Deep Neural Networks)
这些方法各有特点,在不同类型的数据和任务中有不同的优势。比如,决策树具有较好的可解释性,适合用于教学和业务规则提取;而神经网络则擅长处理复杂的高维数据。

3.2 集成分类器(Ensemble Classifiers)
集成分类器是通过组合多个基础分类器的结果来提高整体分类性能的一种方法。
常见的集成方法包括:
Bagging:通过对数据进行多次自助采样(Bootstrap),训练多个模型后进行投票。
Boosting:通过不断提升对难分类样本的关注,使模型逐步改进。
随机森林(Random Forest):在 Bagging 基础上引入特征随机选择,是目前应用非常广泛的集成方法之一。
集成方法一般比单一分类器具有更好的鲁棒性,尤其在数据噪声较大或模型容易过拟合的情况下,表现更为稳定。
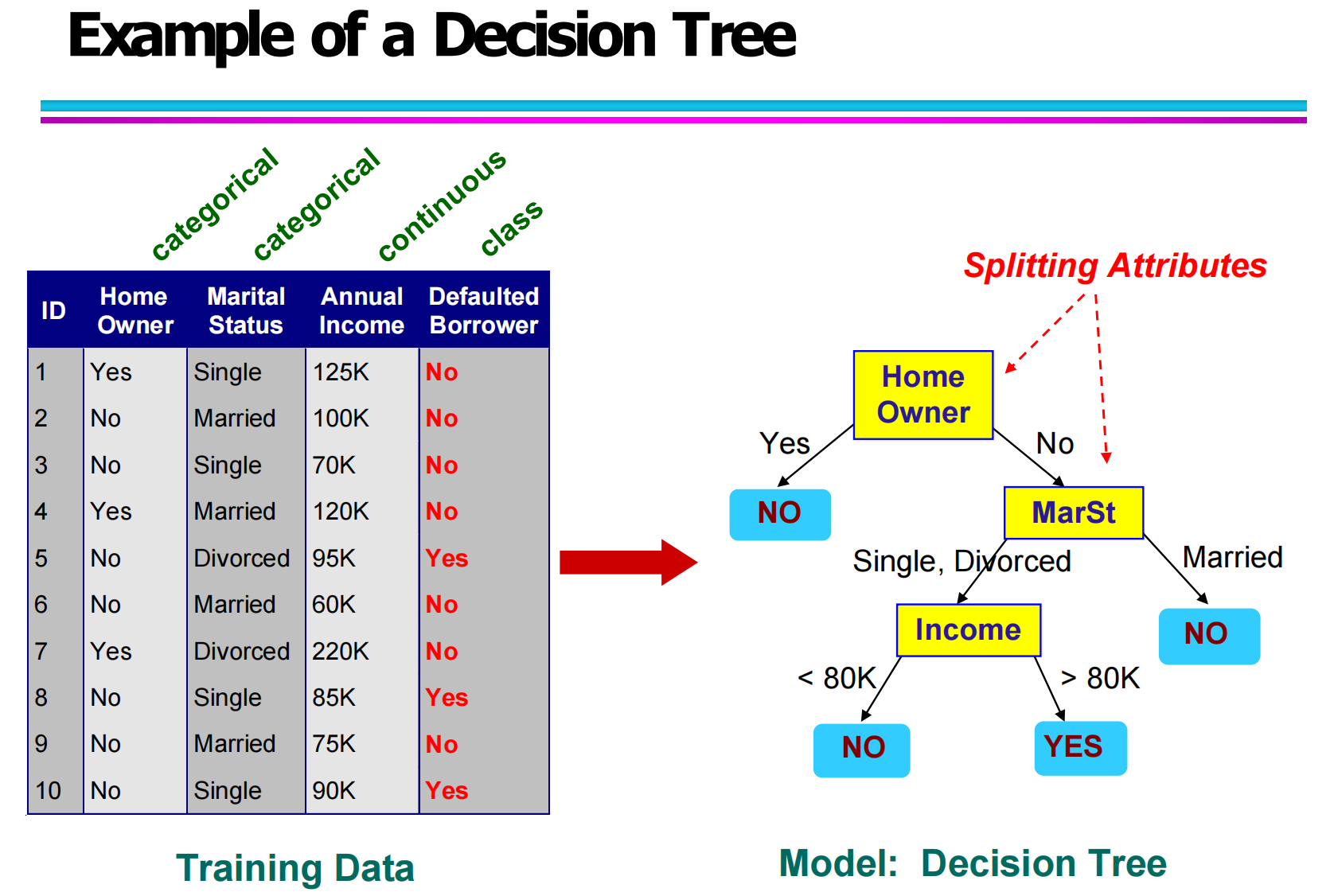
3.3 决策树示例:从数据到模型(Decision Tree Example: From Data to Model)
这一部分重点通过具体示例说明:训练数据是如何一步步转化为一个决策树模型的。
从你给出的训练数据表中可以看到,数据集中包含了多种属性:
Home Owner(是否有房)—— 类别属性
Marital Status(婚姻状态)—— 类别属性
Annual Income(年收入)—— 连续属性
Defaulted Borrower(是否违约)—— 类别标签
在构建决策树时,算法会选择一个最“有区分能力”的属性作为划分节点(Splitting Attribute),然后不断分裂子节点,直到所有样本可以被正确分类或满足终止条件。
如示例所示:
首先使用 Home Owner 作为根节点
然后在 No 分支下继续划分 Marital Status
再根据 Income 设置连续属性阈值进行划分
最终形成了一棵完整的分类树。
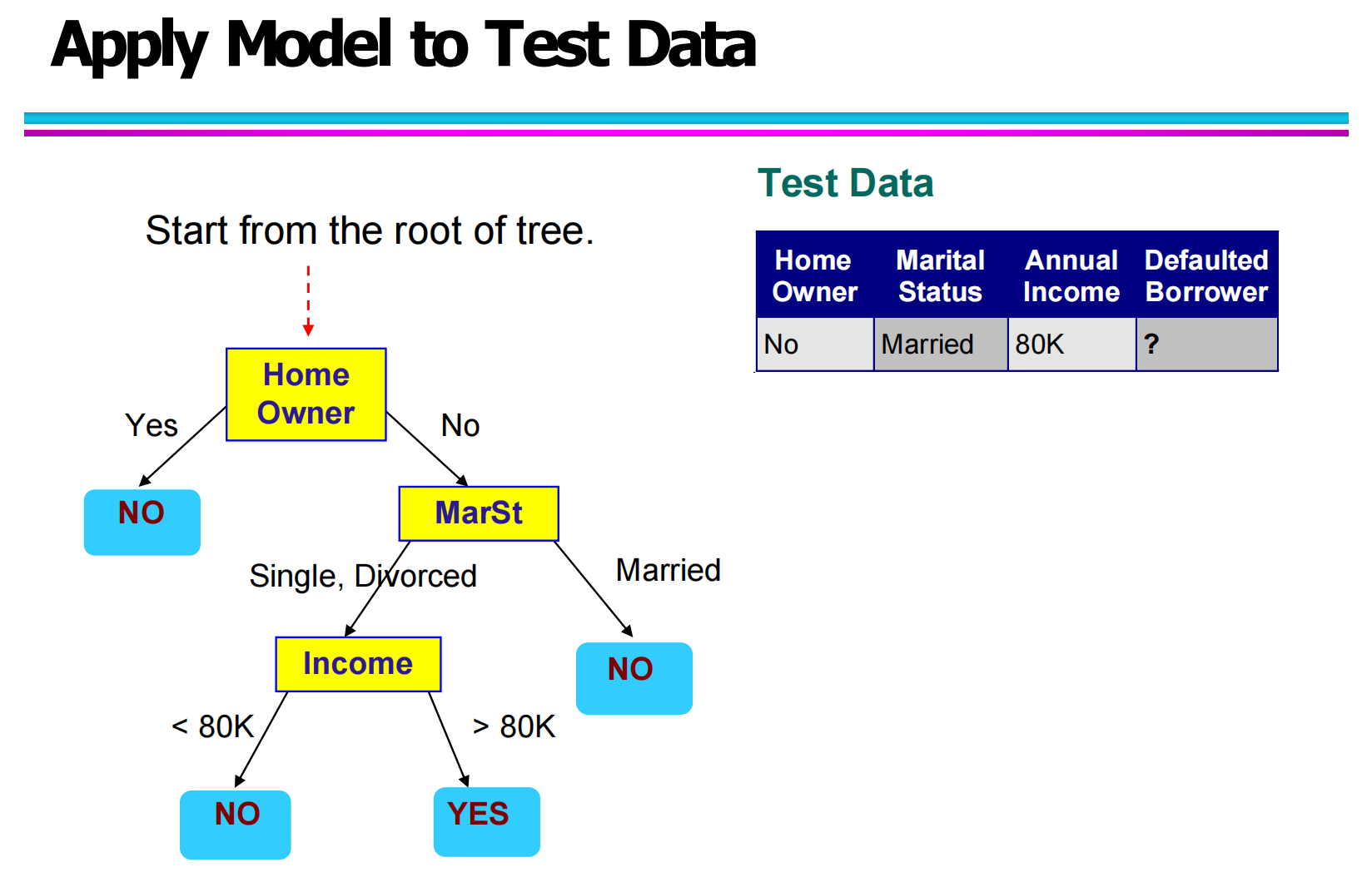
3.4 决策树在测试数据上的应用(Applying Model to Test Data)
当决策树模型构建完成后,就可以将其应用到新的测试数据上进行预测。
在预测时,测试样本会从树的根节点开始,根据自身属性值不断沿着分支向下:
例如:
测试数据为:
Home Owner = No
Marital Status = Married
Annual Income = 80K
决策路径如下:
Root: Home Owner → No
进入 Marital Status → Married
根据训练好的树结构,预测结果为:NO
也就是说,该用户被判定为“不会违约”。
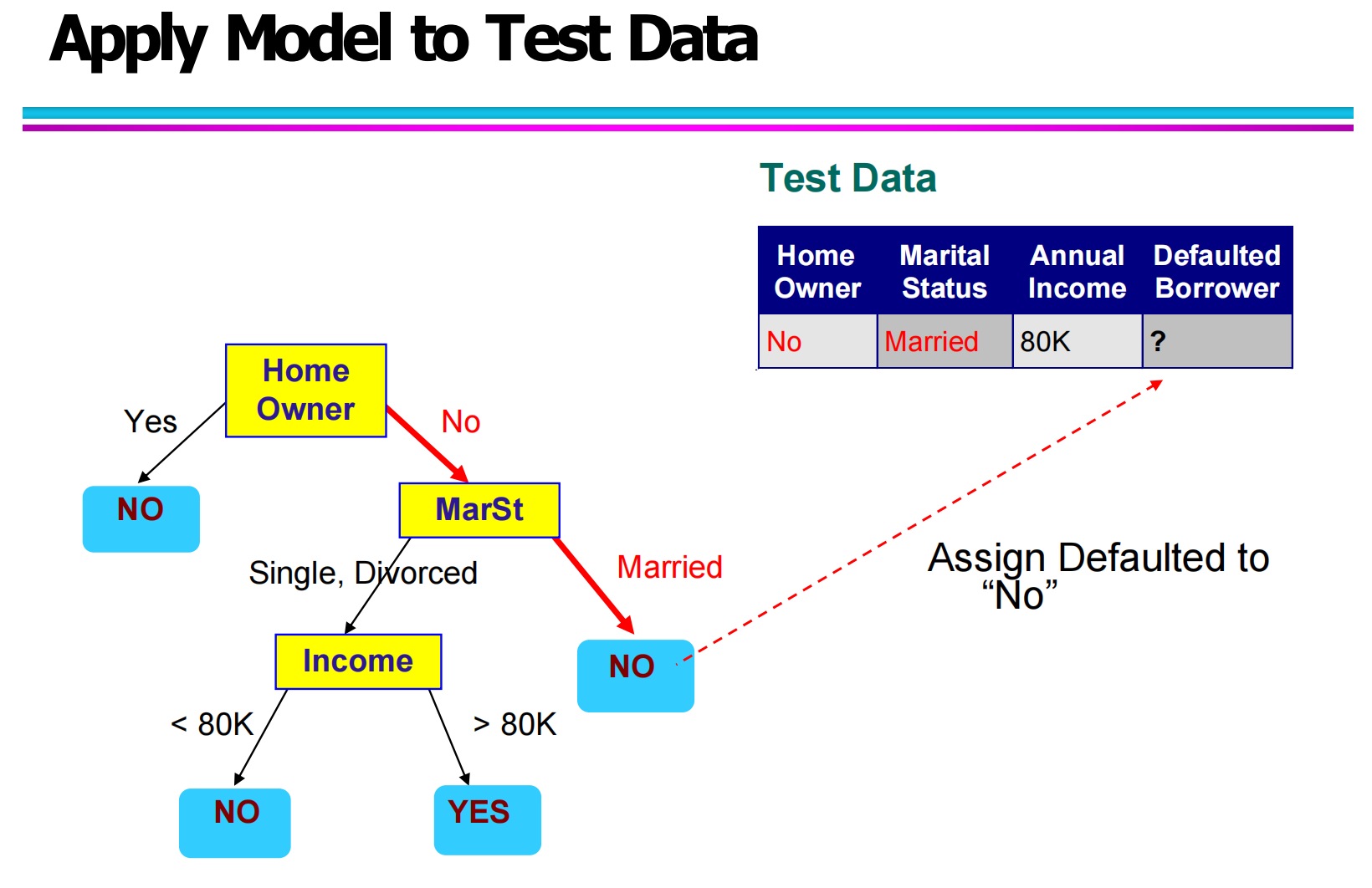
3.5 决策路径可视化演示(Decision Path Visualization)
在另一张图中,清晰标出了红色路径,展示了测试样本从根节点到叶节点的完整推理过程。
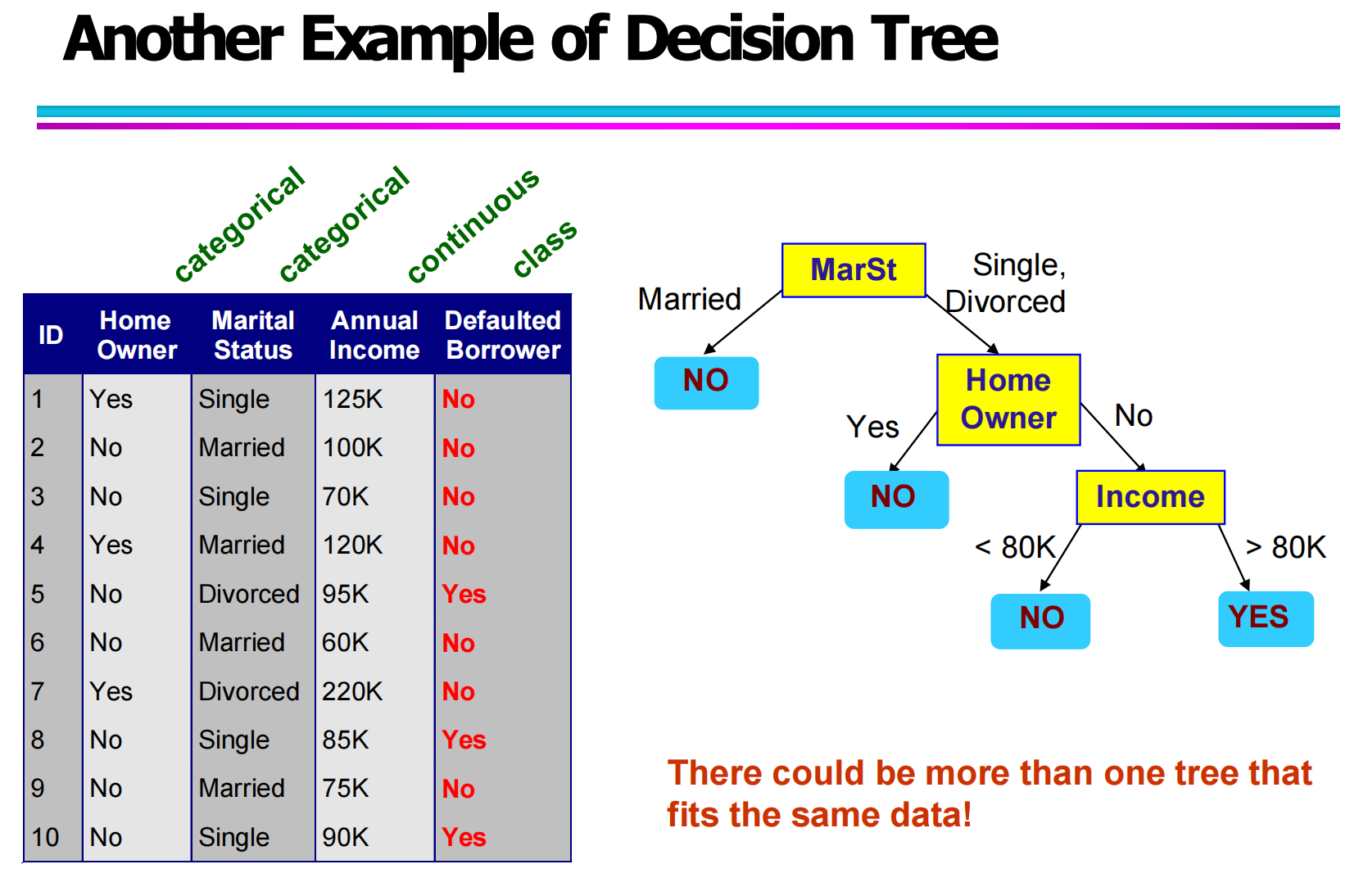
3.6 不同决策树结构的对比(Multiple Decision Trees)
从“Another Example of Decision Tree”这张图可以看出:
对于同一批数据,可能存在多棵不同结构但效果相似的决策树。
这意味着:
决策树不是唯一的
不同属性的划分顺序可能产生不同的树
只要分类效果相近,模型结构不同是完全正常的现象
这也说明,在实际建模中,需要结合模型准确率、复杂度和可解释性综合选择。
3.7 决策树归纳过程(Decision Tree Induction)
决策树的生成过程,在学术上称为“树归纳”(Tree Induction)。
常见的决策树算法包括:
Hunt 算法(Hunt’s Algorithm)
CART
ID3 / C4.5
SLIQ / SPRINT
这些算法本质上都是通过不同的划分策略,递归地构造树结构。例如:
ID3 和 C4.5 使用信息增益或增益率
CART 使用基尼指数(Gini Index)
SLIQ 和 SPRINT 针对大规模数据进行了优化
他们共同的目标是:
在保证分类效果的前提下,尽可能构造出结构合理、避免过拟合的决策树。

四、决策树生成算法(Decision Tree Induction Algorithms)
4.1 Hunt 算法的一般结构(General Structure of Hunt’s Algorithm)

在决策树的构建过程中,Hunt 算法(Hunt’s Algorithm)是一种最早提出、也是最基础的决策树生成框架之一。它的核心思想是:通过递归地对训练数据进行划分,不断生成子节点,直到满足停止条件为止。
在图中,假设 Dt 表示当前到达节点 tt 的训练样本集合,则整个算法遵循以下基本逻辑:
首先,如果当前节点的所有样本都属于同一个类别,那么这个节点直接被标记为叶子节点,其类别即为该类别。这种情况下,不需要再继续划分。
如果 DtDt 中仍然包含多个类别的样本,那么就需要选择一个合适的属性作为划分依据,通过该属性将数据集划分成若干个子集,并对每个子集递归地继续执行相同的过程。
这也是图中“?”节点所表示的含义:当前需要选择最佳的划分属性,使数据不断变得更加“纯净”,最终形成分类树。
4.2 Hunt 决策树构建示例(Example of Hunt’s Algorithm)
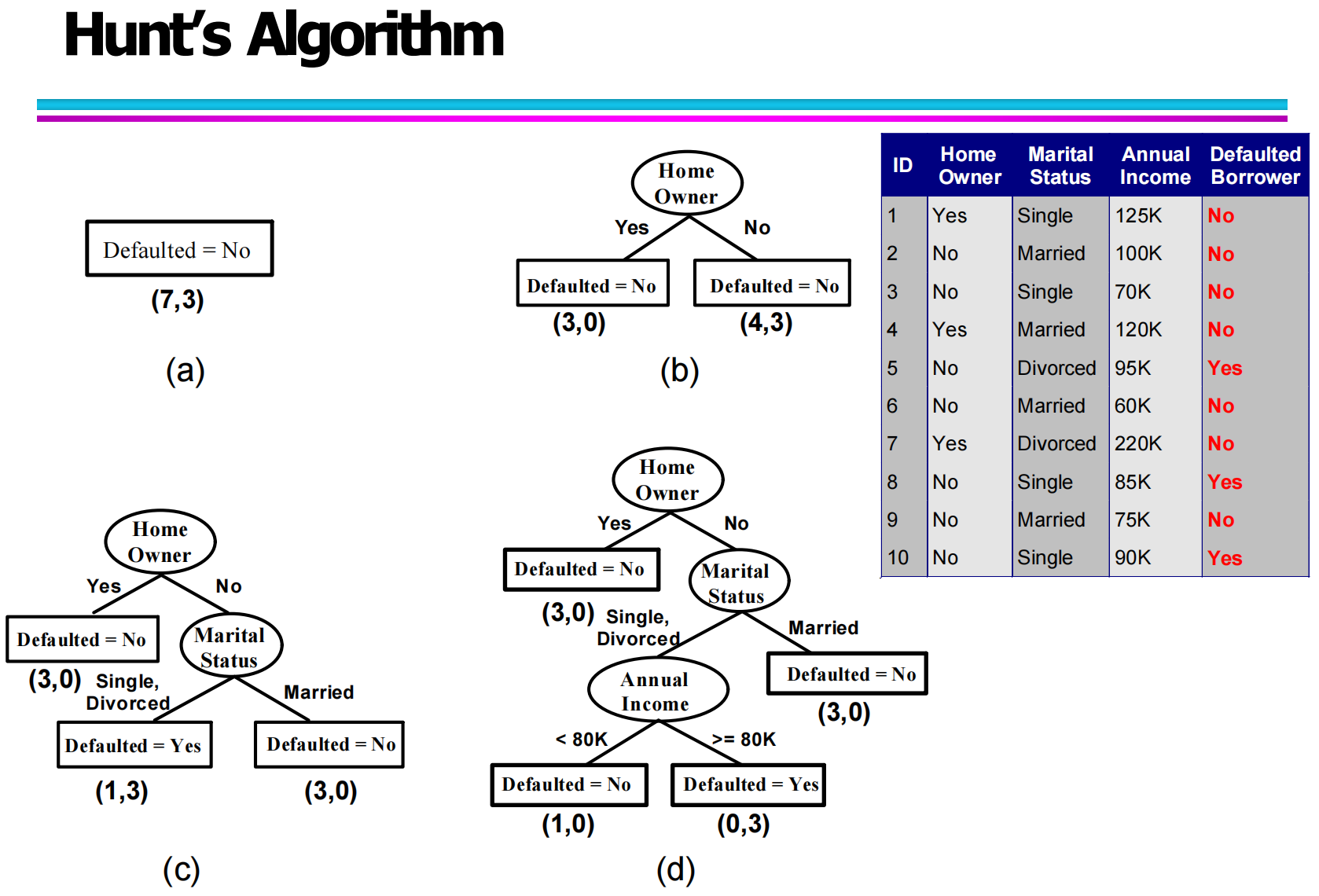
为了更好地理解 Hunt 算法的执行过程,可以结合图中的示例。
在这个例子中,训练数据包含多个属性:
Home Owner(是否有房)
Marital Status(婚姻状态)
Annual Income(年收入)
Defaulted Borrower(是否违约)
在算法初始阶段,所有样本都处于根节点。首先选择属性 Home Owner 进行划分:
当 Home Owner = Yes 时,样本全为 “No”(无违约),因此形成一个叶子节点。
当 Home Owner = No 时,样本中仍然存在 “Yes” 和 “No”,说明数据尚未纯净,需要继续划分。
接着,选择 Marital Status 进一步划分:
若 Marital Status = Married,则全部为 “No”,形成叶节点。
若为 Single 或 Divorced,则进入下一层,继续用 Annual Income 进行区分。
最后,通过 “收入是否大于等于 80K” 作为划分条件,最终得到完整的决策树。
这个过程展示了:
Hunt 算法通过不断选择属性,将复杂问题逐层拆解,直到分类结果足够明确。
4.3 决策树设计问题(Design Issues of Decision Tree Induction)

在实际构建决策树时,除了算法本身,还会涉及几个关键的设计问题:
(1)如何划分训练样本?(How Should Training Records Be Split?)
首先是划分方式的选择。
不同类型的属性需要不同的测试条件表达方式。例如:
对于 离散属性(如性别、婚姻状态),可以直接按不同取值分支;
对于 连续属性(如收入、温度),则需要通过设定阈值进行二分。
此外,还需要使用度量方法来判断某一次划分是否“好”,也就是评估一个属性作为划分依据是否最优。常见的评估指标包括信息增益、基尼指数等,这些通常用于比较不同属性的划分效果。
(2)什么时候停止划分?(When Should the Splitting Stop?)
如果一直划分下去,决策树可能会变得非常复杂,甚至过拟合。因此必须设置停止条件:
常见的停止条件包括:
当前节点中所有样本属于同一类别;
所有样本在各个属性上的取值完全相同;
节点样本数量小于某个阈值;
达到预设的最大树深度。
此外,还可以使用提前终止(Early Termination)策略,在某些情况下提前停止划分,从而避免模型过于复杂。
五、测试条件的表达方法(Methods for Expressing Test Conditions)
在决策树中,内部节点需要通过“测试条件”把样本划分到不同的分支上。测试条件的设计并不是随意的,而是高度依赖于属性本身的类型。一般来说,我们会把属性分为二元属性(Binary)、名义属性(Nominal)、有序属性(Ordinal)和连续属性(Continuous)四类,不同类型对应不同的测试方式。只有根据属性类型选择合适的测试条件,决策树才能既表达足够复杂的划分,又保持结构清晰、易于解释。

这一章就围绕这四类属性,分别介绍在构造决策树时常见的测试条件设计方法,并结合示意图说明多路划分和二元划分的直观含义。
5.1 名义属性的测试条件(Test Condition for Nominal Attributes)
名义属性是指取值之间没有自然顺序的类别型属性,例如“婚姻状态”可以是 Single、Divorced、Married,但这三个值之间不存在大小或先后关系。对于名义属性,最直接的做法是进行多路划分:把每一个不同取值都作为一条分支,这样一个节点就可以被分成若干个子节点,每个子节点对应一个具体取值。这种方式信息表达完整,但当取值种类很多时,树会变得非常“分叉”,可能影响后续学习和理解。
另一种常见做法是采用二元划分,把若干取值归入一个子集,其余归入另一个子集,从而把名义属性转换成“属于某个集合 / 不属于某个集合”的二元测试。比如“婚姻状态”可以分成 {Married} 和 {Single, Divorced},也可以分成 {Single} 和 {Married, Divorced} 等不同组合。不同的划分会得到不同的子集分布,进而影响信息增益或基尼指数等评价指标。
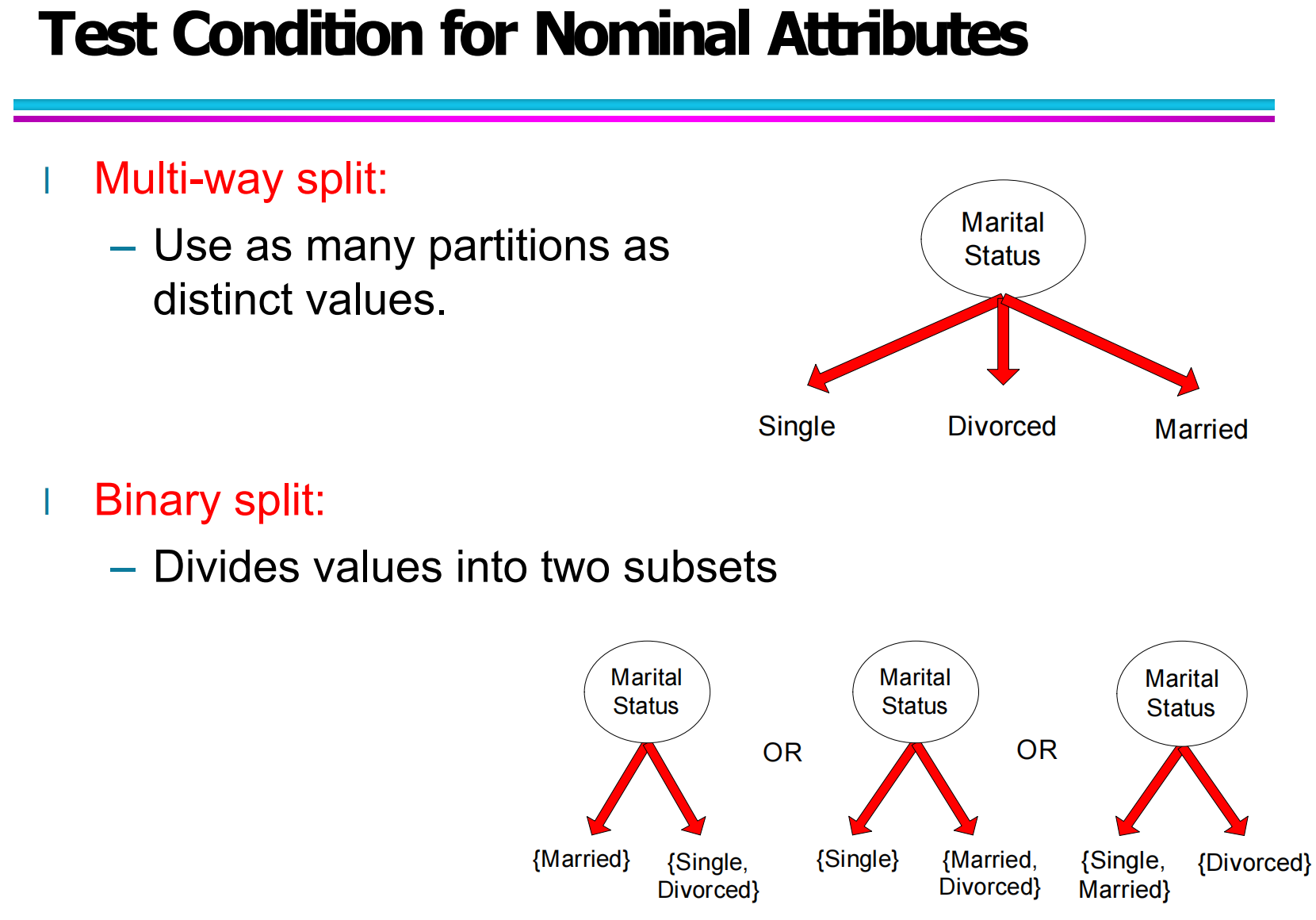
通过名义属性示例可以看出,设计测试条件不仅关乎“能不能划分”,更关乎“划分得好不好”,这也为后面讨论评价指标做了铺垫。
5.2 有序属性的测试条件(Test Condition for Ordinal Attributes)
有序属性与名义属性不同,取值之间存在天然的顺序关系,但具体间隔未必等距。典型例子是衣服尺码:Small、Medium、Large、Extra Large 等。对这种属性来说,我们在设计测试条件时既要利用“离散的类别”,又要尽量保持原有的顺序结构。
类似名义属性,有序属性也可以采用多路划分,把每个不同的尺码值分成单独的分支。不过在实际决策树中,更常用的是二元划分:将连续的一段有序取值放到同一侧,把剩下的取值放到另一侧。比如可以划分为 {Small, Medium} 与 {Large, Extra Large},或者 {Small, Large} 与 {Medium, Extra Large} 等组合。关键点是,合理的分组应当尊重原始顺序,让一侧的取值在序列上“连续”,而不是打乱顺序。
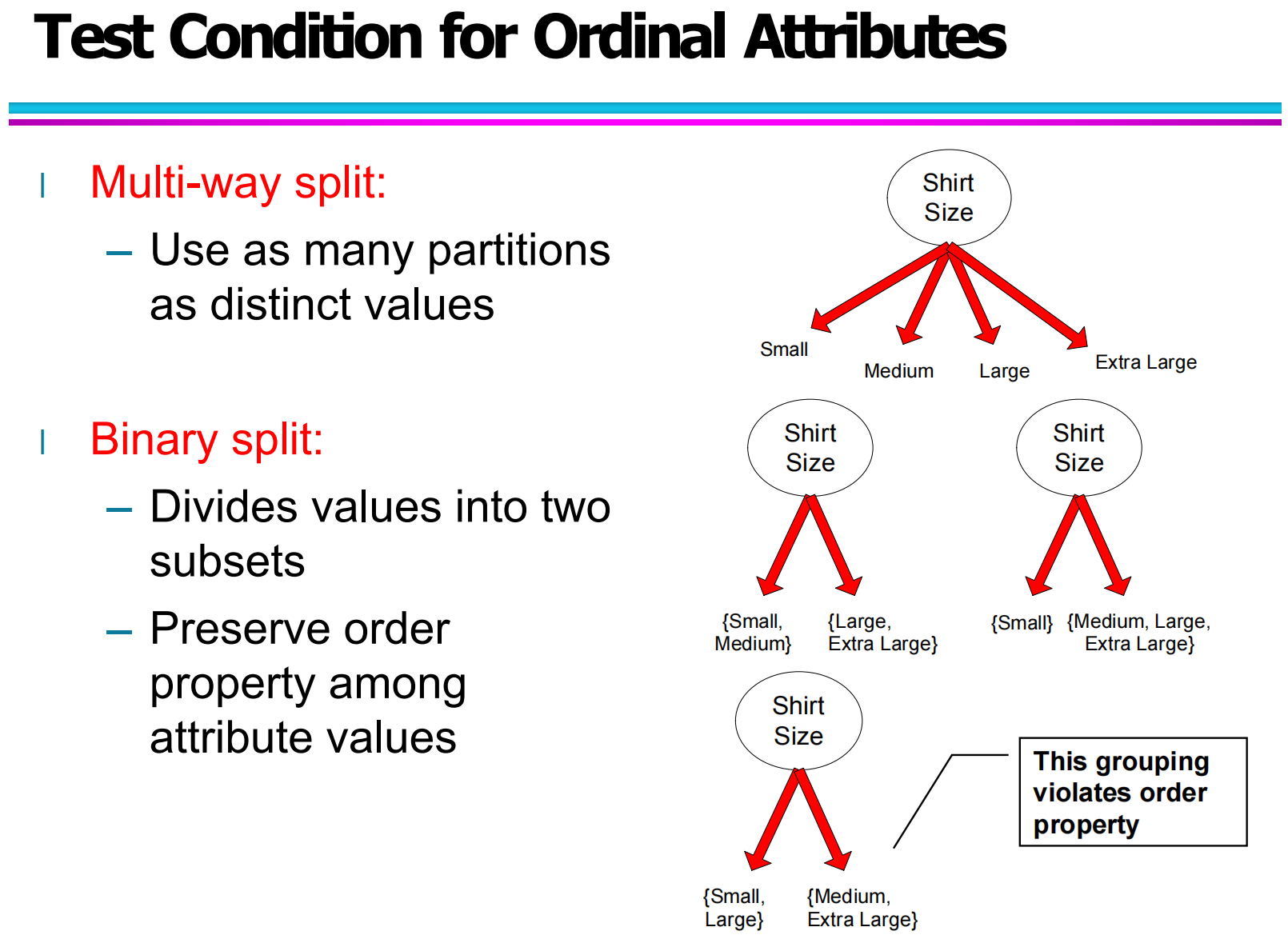
如果二元划分随意把 Small 和 Large 放在一起,而把 Medium 与 Extra Large 放在另一边,就破坏了原来的大小关系,后续节点再想利用“从小到大”的趋势就会变得困难。因此,有序属性在测试条件设计上,需要显式考虑顺序信息,而不仅仅是“类别不同”。
5.3 连续属性的测试条件(Test Condition for Continuous Attributes)
连续属性的取值范围通常是实数区间,例如“年收入”、“温度”、“时间”等,理论上可以取无穷多个不同的值。这种情况下,多路划分显然不现实,我们必须将连续属性离散化为区间,并在此基础上构造测试条件。
最常见的一种方式是二元阈值划分:选择一个阈值 vv,然后用“属性值是否大于(或小于等于)该阈值”来把样本分成两部分。例如把“年收入>80K?”作为测试条件,那么所有收入大于 80K 的样本沿一条分支,其他样本沿另一条分支。通过在不同节点使用不同的阈值,决策树可以逐步刻画连续属性上的复杂边界。
在某些场景下,也会采用多区间划分:先将连续区间分割成若干个子区间,再让每个区间对应一条分支。如把年收入分成 [0,10K)、[10K,25K)、[25K,50K)、[50K,80K)、(80K,∞) 等若干段,每一段代表不同收入层次。这样做可以一次性产生更多、更细粒度的划分,但同样会让树的分支数变多。

无论采用哪种方式,核心都是把原本连续的数轴切成若干片段,让决策树可以像处理离散属性一样进行路径选择。
5.4 基于连续属性的划分策略(Splitting Based on Continuous Attributes)
在具体实现中,连续属性除了直接用阈值划分外,还可以先整体做离散化,再在离散化后的结果上构造测试条件。离散化可以看做把连续属性转成一种特殊的有序属性,常用的做法包括等宽分箱、等频分箱以及基于聚类的分箱等。若在决策树构造之前就统一进行一次离散化,这被称为静态离散化;若在每个节点根据当前数据分布重新寻找最优切分点,则属于动态离散化。

另一种思路是不做显式分箱,而是让算法在训练过程中自动搜索所有可能的切分点,并根据信息增益或基尼指数等指标选择最好的阈值。这样的二元决策形式通常写成 A<v 或 A≥v,其中 v 是候选阈值。由于可能的阈值很多,这种做法在计算上会比离散化稍微重一些,但往往能够得到更细致、拟合更好的划分边界。
综合来看,针对连续属性,我们既可以通过离散化把问题转化为有序属性划分,也可以直接在原始数轴上进行二元切分。不同策略在模型精度和计算成本之间做出不同权衡,实际使用时通常结合数据规模、噪声程度和应用需求来选择。
六、最优划分的确定(How to Determine the Best Split)
6.1 最优划分问题引入(Introduction to Best Split)
在决策树构建过程中,当一个节点包含属于多个类别的样本时,就需要选择一个属性进行划分。不同属性的划分方式不同,带来的分类效果也不同。

如图所示,在一个包含 20 条记录的数据集中,类别分布为:
类别 C0:10 条
类别 C1:10 条
若直接分类,误差较大,因此必须进行属性划分。
图中分别对 Gender (性别)、Car Type (汽车类型) 和 Customer ID (客户编号) 进行划分,不同属性产生的子节点纯度明显不同。
Gender 产生两个子节点:
(C0: 6, C1: 4)
(C0: 4, C1: 6)
Car Type 产生三个子节点,且其中某些节点非常“纯”
Customer ID 虽然每个子节点都很纯,但会产生过多分支,容易导致过拟合。
因此,需要一个量化标准去判断:谁才是“最优划分”。
6.2 贪心策略(Greedy Strategy)

决策树采用的是一种贪心方法(Greedy Approach):
在每个节点,只选当前最优,不回溯整体。
核心思想:
优先选择能够使子节点“类别更纯(purer)”的属性划分。
比如:
(C0:5, C1:5) → 不纯度高
(C0:9, C1:1) → 不纯度低
后者显然更适合作为划分结果。
因此,需要引入“节点不纯度”的概念来量化当前节点和子节点的分类混乱程度。
6.3 节点不纯度度量(Measures of Node Impurity)

常见的三种节点不纯度度量方式:
(1)基尼指数(Gini Index)
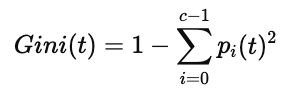
其中:
pi(t):节点 t 中类别 i 的比例
c:类别总数
特点:
数值越小,节点越纯
决策树 CART 常使用此指标
(2)信息熵(Entropy)
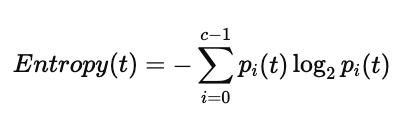
特点:
熵越小,不确定性越低
ID3 / C4.5 算法常用
(3)分类误差(Misclassification Error)
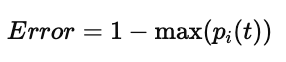
特点:
计算简单
对节点微小变化不敏感
一般较少用于选择分裂属性
6.4 最优划分计算流程(Finding the Best Split)

完整的属性选择过程如下:
计算划分前节点不纯度 P
根据当前节点的类别分布,计算 Gini / Entropy 等指标。针对每个属性进行划分
按照该属性的不同取值(或二分方式)生成若干子节点。计算每个子节点的不纯度
计算加权不纯度 M
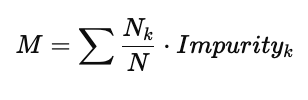
其中:
Nk:第 k 个子节点样本数
N:总样本数
Impurityk:子节点不纯度
计算信息增益 / 不纯度下降量
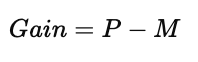
选择 Gain 最大的属性进行划分
等价描述:
也可以说是选择 加权不纯度 M 最小的属性。
6.5 通过示意图理解最优选择
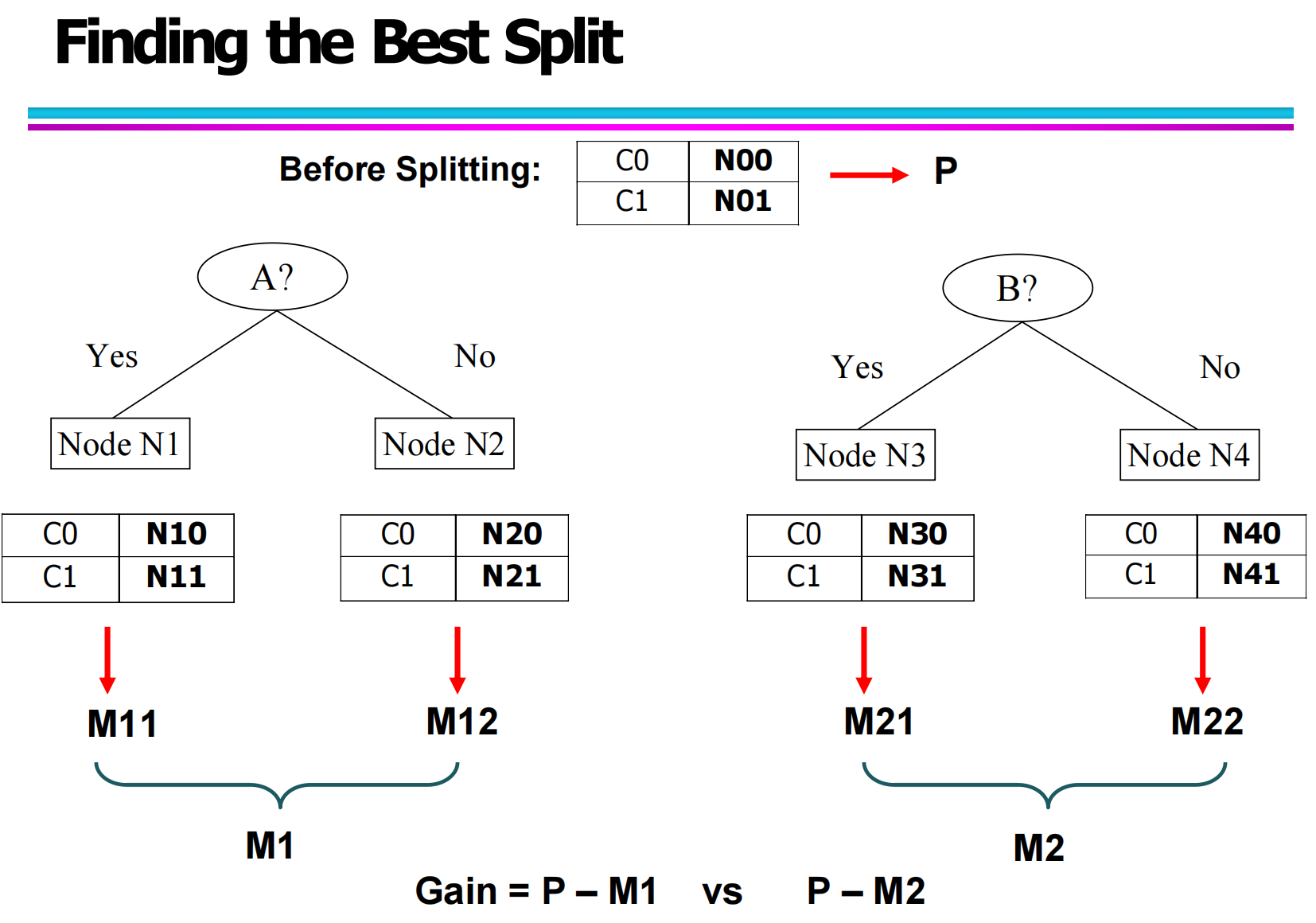
在图中:
当前节点不纯度为 P
对属性 A 划分后得到左右两个子节点,其不纯度分别为 M11,M12,总不纯度为 M1
对属性 B 划分后得到两个子节点,其不纯度分别为 M21,M22,总不纯度为 M2
比较结果:
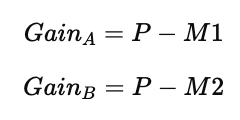
若:
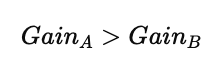
则选择属性 A 作为当前节点的最优划分属性。
