一、什么是数据预处理(Introduction to Data Preprocessing)
在机器学习或数据挖掘中,我们常听到一句话:“数据质量决定模型上限”。
这句话背后的核心,其实就是数据预处理(Data Preprocessing)。
在真正建模之前,我们拿到的数据往往是杂乱的、不完整的、有噪声的,如果直接丢给模型训练,得到的结果通常不稳定、误差大,甚至完全没有参考价值。所以,在课程中,数据预处理被称为机器学习流程中最容易被忽略、但最重要的一步。
1.1 数据预处理是什么?
从课程角度来看,数据预处理是指:
在对数据进行建模和分析之前,对原始数据进行整理、转换和优化的一系列操作,目的是让数据变得:
更干净(减少噪声和异常值)
更规则(统一格式和尺度)
更适合算法处理(减少维度、提取特征等)
简单理解就是:
把“乱糟糟的原始数据”变成“模型能看懂的标准数据”。
1.2 数据预处理在整个流程中的位置
在完整的数据挖掘流程中,一般分为:
数据采集
数据预处理
特征工程
模型训练
模型评估
其中,数据预处理是承上启下的一步,它既连接了“原始数据获取”,又为后续的“特征工程与模型训练”打下了基础。
如果预处理做得不好,后面的特征再好、模型再复杂,效果也会大打折扣,这也是为什么课程中老师会反复强调:
数据预处理往往比模型本身更重要。
1.3 数据预处理的七个核心内容

图中一共列出了7 个预处理核心模块:
Aggregation(数据聚合)
Sampling(数据采样)
Discretization and Binarization(离散化与二值化)
Attribute Transformation(属性变换)
Dimensionality Reduction(降维)
Feature Subset Selection(特征子集选择)
Feature Creation(特征构造)
这 7 个点,构成了你这篇博客的整体技术主线,后面每一章我都会围绕其中一个点,配合你发来的图片进行详细讲解。
这里可以简单理解为:
这是一张“数据预处理的地图”,后续章节就是对地图中每个模块逐个拆解学习。
二、Aggregation(数据聚合)
2.1 聚合(Aggregation)的基本概念
在数据预处理中,Aggregation(数据聚合)指的是:
将多个属性(attributes)或多个对象(objects)合并为一个新的属性或对象。
这一定义正是图里的第一行核心说明:
Combining two or more attributes (or objects) into a single attribute (or object)
简单理解就是:
把很多“细碎的数据”合并成“更粗粒度的数据”。

2.2 聚合的目的:为什么要做 Aggregation?
根据图上的内容,聚合主要有三个目的:
(1)Data Reduction:减少数据规模
聚合可以减少数据集中样本数量或属性数量。
比如:
原来是每天一个数据 → 聚合后变成每月一个数据
原来是每个用户一次消费 → 聚合成每个用户的消费总额
这样可以:
减少计算量、减少存储需求、提升后续建模效率。
(2)Change of Scale:改变数据的尺度
你图中给了两个典型例子:
城市 → 区域 → 省份 → 国家
天 → 周 → 月 → 年
这是尺度变换最典型的聚合方式。
比如原始数据是按“天”记录的销量,如果研究的是长期趋势,按“月”或“年”更有意义,也更直观。
(3)More Stable Data:使数据更加“稳定”
图中提到一个很重要的概念:
Aggregated data tends to have less variability
意思是:
聚合后的数据通常波动更小,更平滑,更稳定。
比如:
每天的销量可能波动很大,但当你把它们聚合为“月销售额”后,整体趋势就会平滑很多,便于分析长期趋势。
2.3 示例图:从“每日销售”到“月销售额”
图对应的是一个非常标准的聚合案例:
从 Daily Sales → Monthly Sales
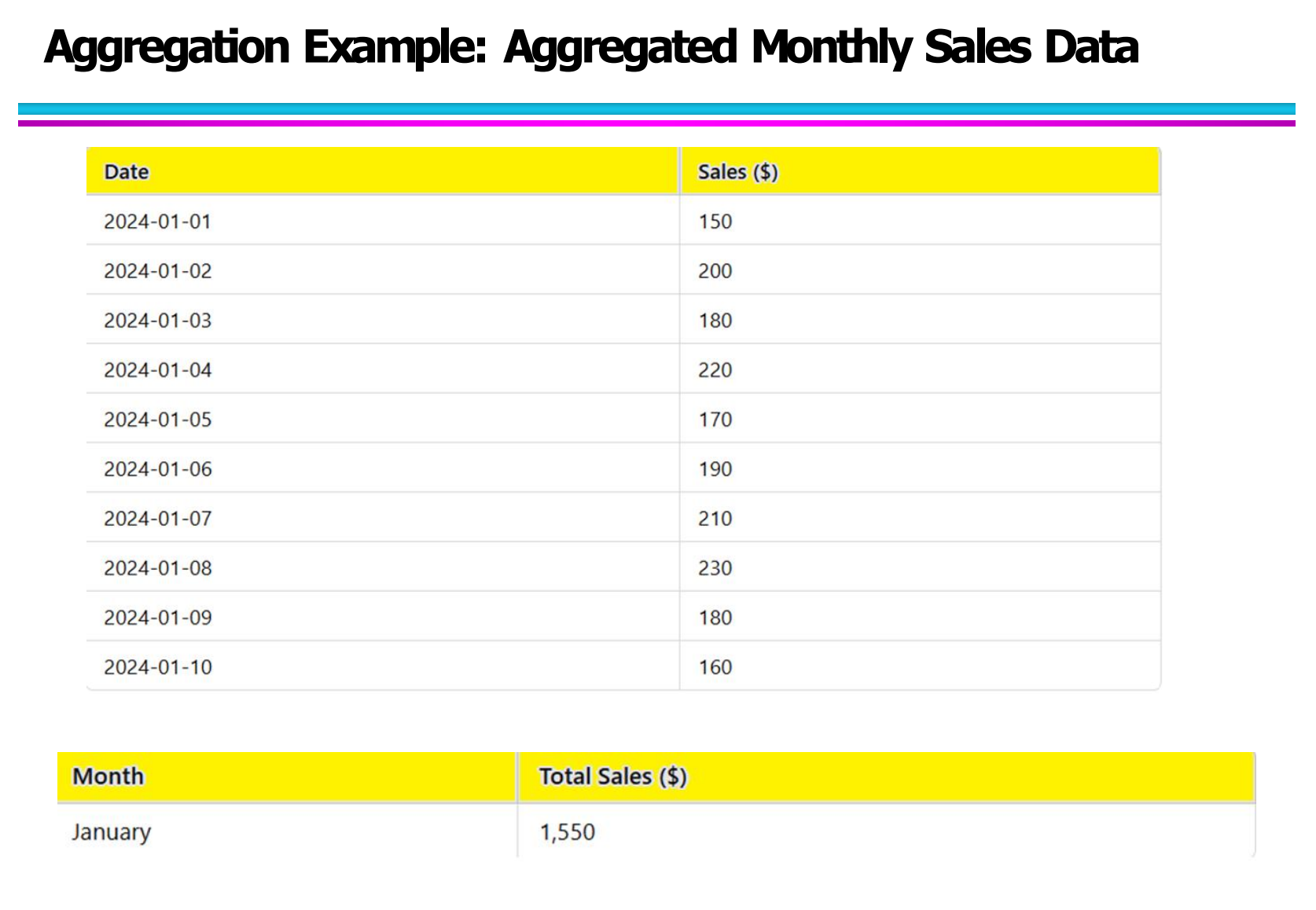
上半部分是每日销售数据:
比如:
这些数据是高频数据(High Granularity),细节多,但波动大。
下半部分是聚合之后的结果:
也就是说,将每天的销售额通过求和(sum aggregation)的方式,整合成了一个“月销售额”。
这样带来的好处包括:
数据更加简洁
更有利于做长期趋势分析
计算复杂度更低
更适合用于后续的预测模型(比如时间序列预测)
三、Sampling(数据采样)
3.1 Sampling 是什么?

这张图里面给了非常清晰的定义:
Sampling is the main technique employed for data reduction.
意思是:
采样是实现数据压缩(Data Reduction)的最主要技术之一。
在实际的数据挖掘中,数据量通常非常庞大:
可能是几百万行、上千万条记录,甚至是实时流数据。
这时候,如果直接使用全部数据进行训练和分析,计算成本非常高,而且往往没有必要。
所以,采样的核心思想就是:
用一部分数据来代表整体数据,从而减少计算量,但尽量不降低分析质量。
3.2 采样适合用在什么场景?
图中还有这一句非常关键的话:
It is often used for both the preliminary investigation of the data and the final data analysis.
意思是:采样既用于:
前期探索性分析(EDA):
比如先用 10% 数据看看分布情况、趋势情况。正式模型分析阶段:
当数据实在太大时,可以对数据进行合理采样再建模。
这在课程实验和项目中都非常常见,比如:
课程项目中先用一小部分数据调试代码
等代码没问题后,再扩大采样规模训练模型
3.3 代表性样本(Representative Sample)的重要性

图中强调了一个特别重要的采样原则:
Using a sample will work almost as well as using the entire data set, if the sample is representative.
意思是:
只要样本是具有代表性的,
使用样本得到的结果,和使用全部数据得到的结果是接近的。
那什么叫“具有代表性”?
你图里给出的定义是:
A sample is representative if it has approximately the same properties (of interest) as the original set of data.
也就是说:
如果原始数据集有 60% 男生,40% 女生,
那一个好的样本中,大概率也应该接近这个比例,而不是 90% 男生或 10% 女生。
3.4 Sample Size(样本大小)的影响

这张图讲的是:
样本量越大,通常越接近整体分布。
图中重点有两点:
更大的样本量 → 更可能准确代表整个总体
当数据具有多个类别时,更大的样本量能确保每个类别都有足够的数据
这点在分类任务中非常关键,比如:
如果数据中有三个类别:A、B、C
但你采样后 C 类只剩 2 条数据,那这个采样就是失败的采样。
3.5 用“点阵图”理解样本规模的影响

你这张图非常直观地展示了采样规模带来的视觉效果变化:
8000 points:基本可以看清完整结构
2000 points:轮廓清晰但细节减少
500 points:结构开始模糊,细节丢失明显
这正好说明了一个结论:
采样规模越小,越容易丢失数据原本的结构信息。
所以在实际应用中,
采样不是越少越好,而是在效率和信息保留之间找一个平衡点。
3.6 Sampling 的常见类型

根据这张图,你的课件中主要介绍了两大类采样方式:
(1)Simple Random Sampling(简单随机采样)
特点:
每个样本被选中的概率相同
常见有两种方式:
Sampling without replacement(不放回抽样)
抽到一个对象后,从总体中移除,不能再次被选中。
Sampling with replacement(放回抽样)
抽到的对象不移除,有可能被再次选中。
简单理解就是:
就像抽扑克牌,一个是抽完不放回,一个是抽完再放回继续抽。
(2)Stratified Sampling(分层采样)
你的图中是这样描述的:
Split the data into several partitions; then draw random samples from each partition.
意思是:
先把数据按照某种规则分组(例如按性别、类别、地区等),
再从每个组中分别进行随机采样。
这个方法的优点是:
能保证每个类别在样本中都有合理比例,避免数据偏差。
在数据不平衡问题中,这是一个非常重要的方法。
3.7 本章小结
用一句话总结第三章的核心思想就是:
Sampling 的本质是用“少量、但有代表性”的数据,去近似描述“整体数据”。
而一份好的采样数据,应当满足:
具有代表性
数据分布接近原始数据
不丢失重要结构信息
四、Discretization(离散化)
4.1 离散化的基本概念
在数据预处理中,离散化(Discretization) 是指:
将一个连续型属性(continuous attribute)转换为有序的类别属性(ordinal attribute)的过程。
通俗来说:
原本连续的数据取值范围是无限或非常多的,
离散化就是把这些取值映射到有限个区间或类别中,
从而简化数据表示,降低模型复杂度。
离散化具有以下特点:
一方面减少了连续数据的噪声影响,
另一方面也让一些离散算法(如决策树)更容易处理。

4.2 数据分箱(Data Partitioning)思想
在实际中,离散化经常通过分箱(binning)来实现。
其核心思想是:
将一个连续属性的数据范围,划分为若干个区间(bins),
然后把属于同一区间的数据归为一个类别。
数据分箱在无监督离散化中主要有三种常见方式:
等宽分箱(Equal Width Partitioning)
等频分箱(Equal Frequency / Equi-depth Partitioning)
基于聚类的分箱(如 K-means Discretization)

4.3 无监督离散化方法一:等宽分箱(Equal Width)
等宽分箱的核心思想是:
将数据取值范围均分为若干个等宽的区间。
其区间宽度公式为:
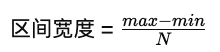
其中:
max 是数据最大值
min 是数据最小值
N 是分箱数量
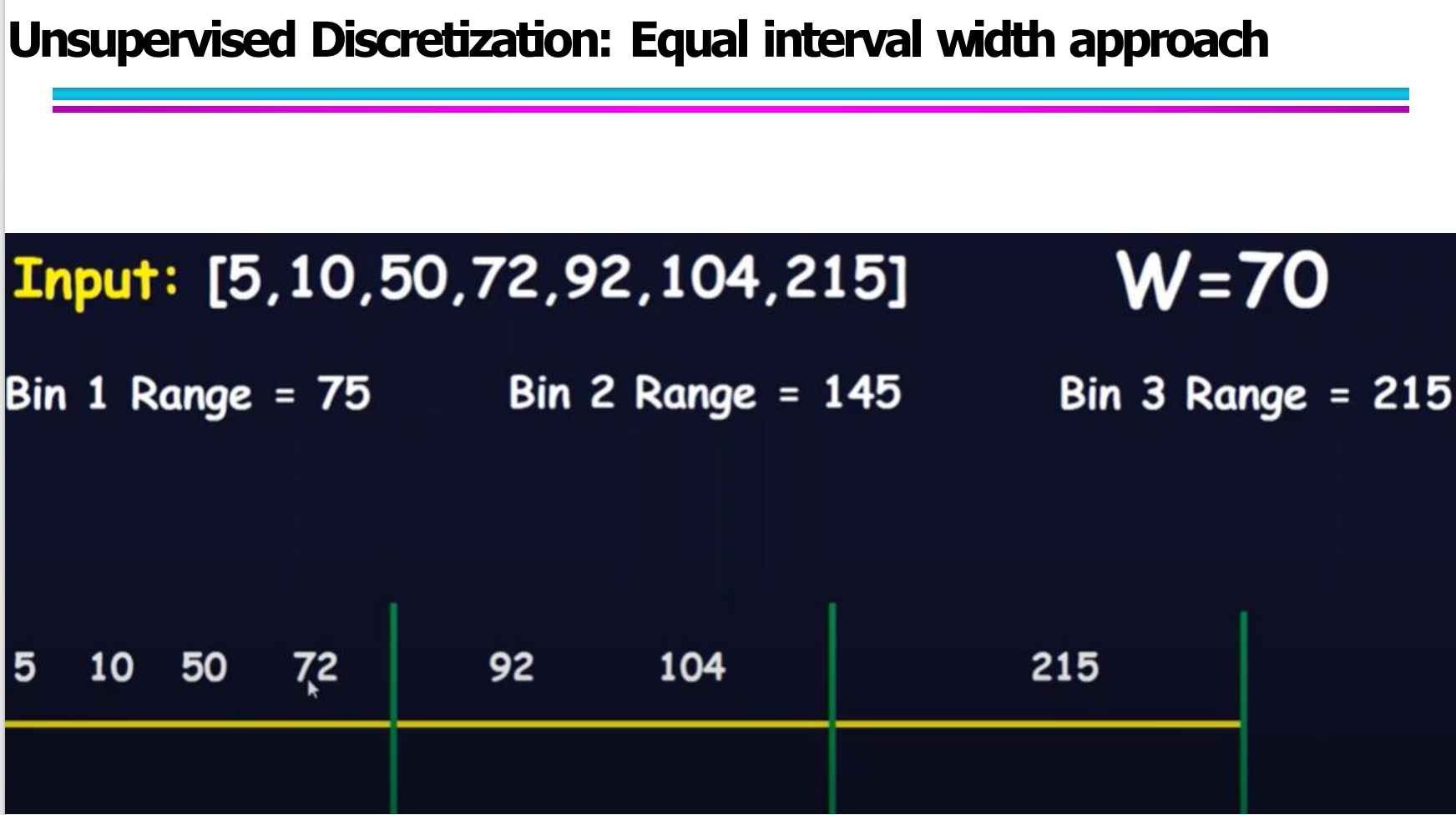
比如示例数据:[5, 10, 50, 72, 92, 104, 215]
如果分成 3 个箱子:
区间宽度 = (215 - 5) / 3 = 70
那么分区间为:
Bin1: [5, 75]
Bin2: (75, 145]
Bin3: (145, 215]
之后再把每个数据按数值大小分配到对应区间。



4.4 无监督离散化方法二:等频分箱(Equal Frequency / Equi-depth)
等频分箱与等宽分箱不同,它不关注每个区间的数值跨度,
而是强调:每个 bin 中的数据数量大致相同。
操作步骤如下:
第一步:对数据进行排序
第二步:将排序后的数据按“每个 bin 包含相同数量数据”的方式划分
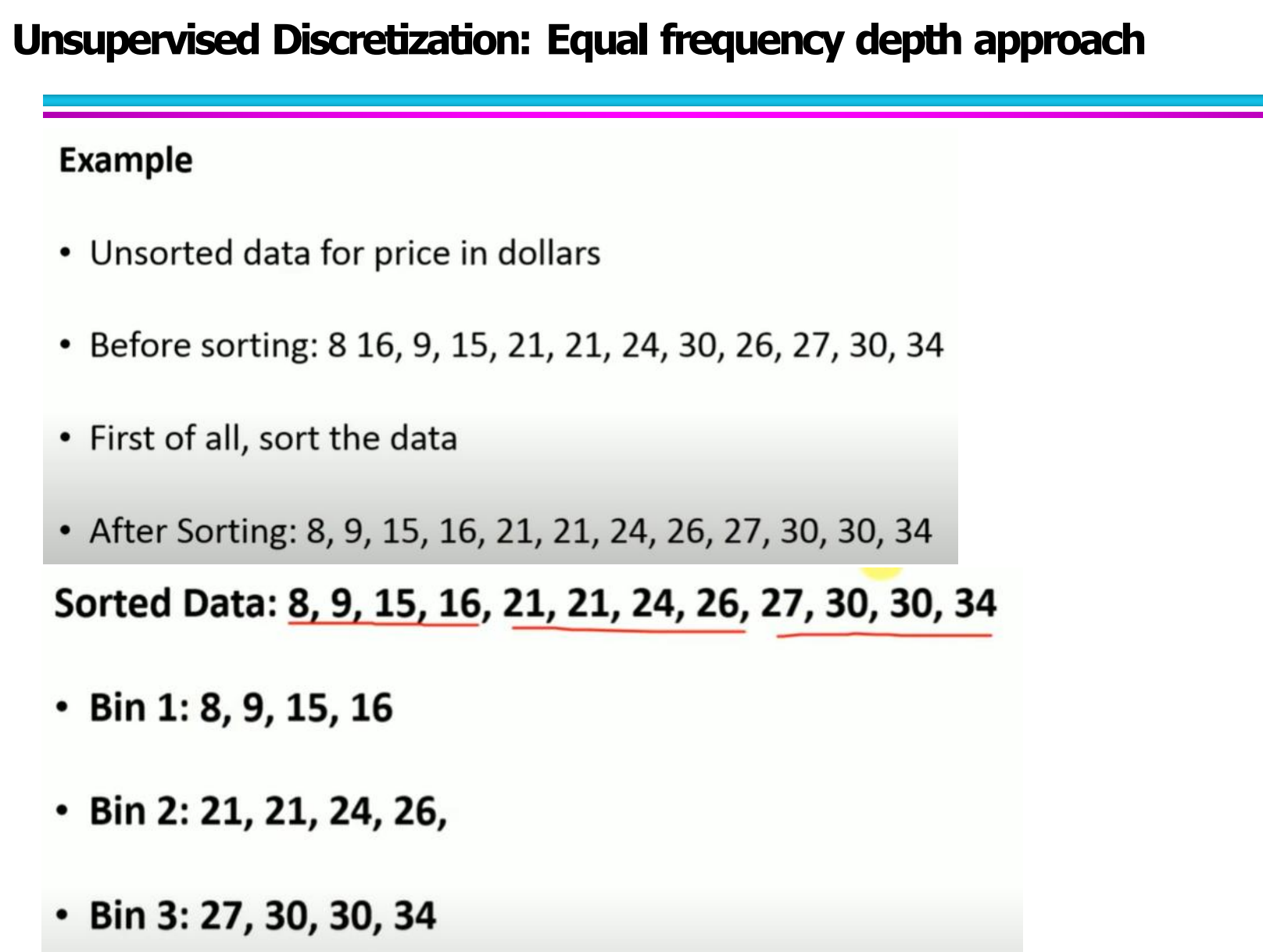
例如数据:[8, 16, 9, 15, 21, 21, 24, 30, 26, 27, 30, 34]
排序后为:[8, 9, 15, 16, 21, 21, 24, 26, 27, 30, 30, 34]
如果设置 3 个 bins,则每个 bin 包含 4 个数据:
Bin1: 8, 9, 15, 16
Bin2: 21, 21, 24, 26
Bin3: 27, 30, 30, 34
这种方式每个区间中的样本数量非常均衡,但每个区间的数值跨度可能并不均等。



4.5 无监督离散化方法三:K-means 离散化
等宽和等频都是基于规则划分,而 K-means 离散化 则是利用聚类思想进行分箱,更偏向数据驱动。
具体思想是:
先利用 K-means 聚类算法,把数据分成 K 个簇,
然后将每一个簇看作一个“箱子”(bin),
从而实现离散化。
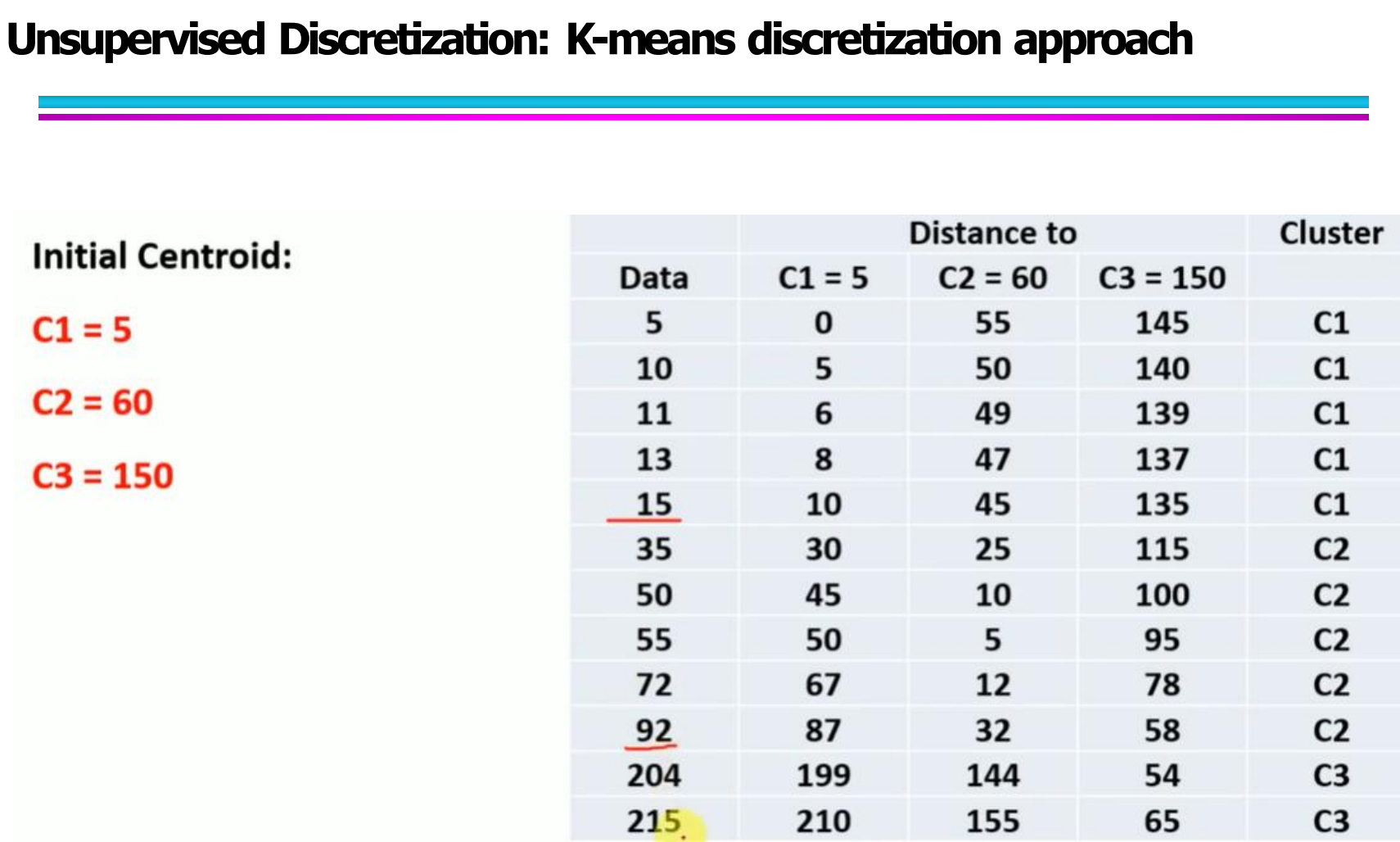
在例子中:
初始质心设置为:
C1 = 5, C2 = 60, C3 = 150
然后计算每个数据点到三个质心的距离,
根据最小距离归类到对应的簇,例如:
5, 10, 11, 13, 15 → 分到 C1
35, 50, 55, 72, 92 → 分到 C2
204, 215 → 分到 C3
每个 cluster 最终就相当于一个离散区间。
相比等宽和等频,K-means 离散化的优点是:
它能根据数据本身分布特点形成更“自然”的区间。

4.6 Binarization(二值化)
二值化是一种特殊形式的数据转换方法,它的目标是:
将连续属性或类别属性映射为一个或多个二值变量(binary variables),也就是用 0 和 1 来表示原始数据的信息。
图中的定义是:
Binarization maps a continuous or categorical attribute into one or more binary variables.
这句话的核心意思是:
无论原始属性是连续的还是离散的(类别型),都可以通过二值化的方式,变成若干个只包含 0/1 的属性。
4.6.1 类别属性的二值化
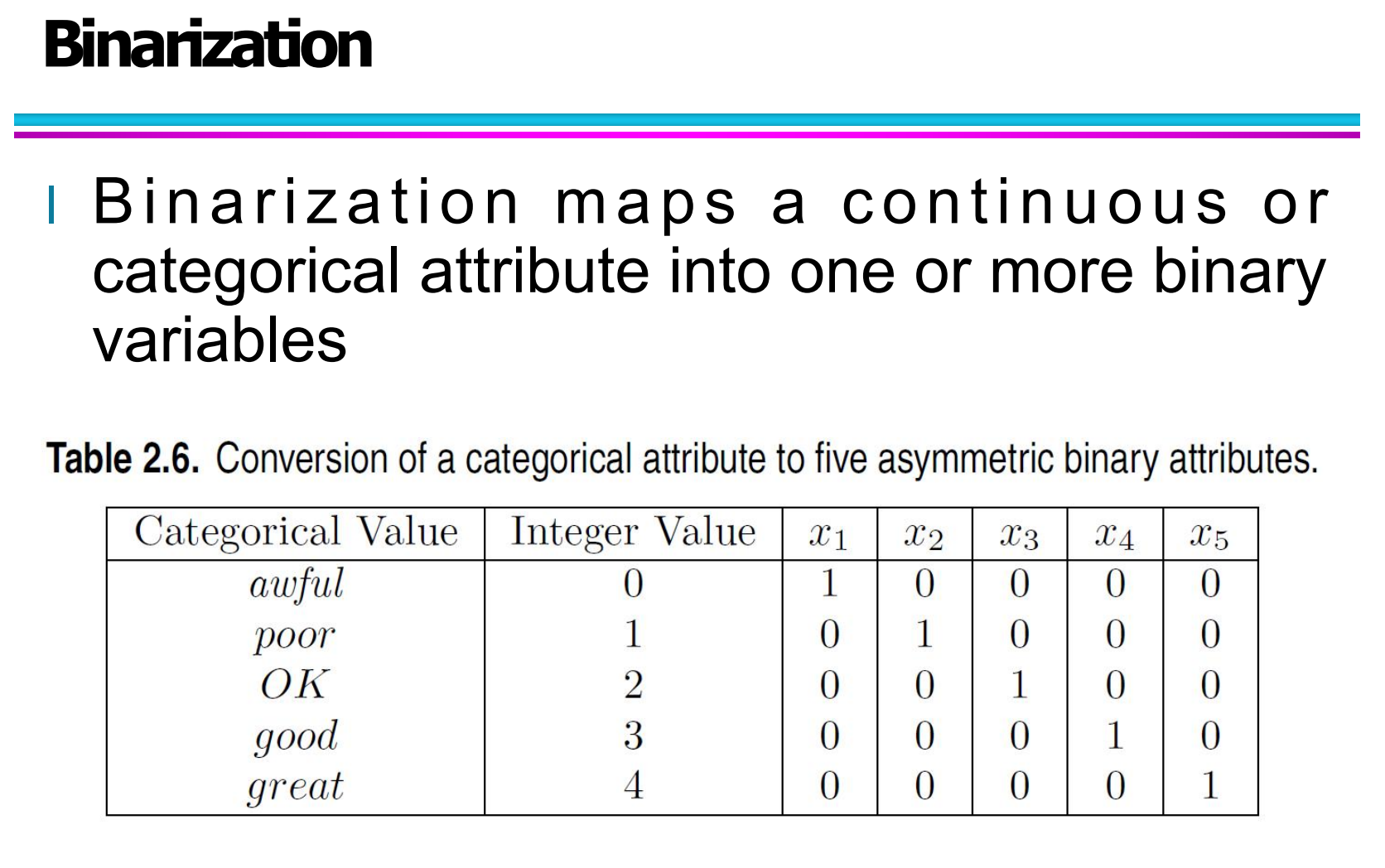
在表格中,展示了一个典型的:
将一个多类别属性转换为多个非对称二值属性(asymmetric binary attributes) 的过程。
原始类别属性如下:
awful
poor
OK
good
great
如果直接用一个整数编码:
awful → 0
poor → 1
OK → 2
good → 3
great → 4
虽然方便存储,但这个整数并不表示真实的“数值大小”关系,直接用在很多算法中会引入误导。
因此,二值化的做法是:
把这一个属性,拆成 5 个二值属性:x1, x2, x3, x4, x5。
例如:
当评分为 awful:
→ x1=1,其余为0当评分为 good:
→ x4=1,其余为0当评分为 great:
→ x5=1,其余为0
这样做的好处是:
避免引入虚假的大小关系(避免算法误认为 great 比 awful 大 5 倍)。
更适合用于很多机器学习算法,比如逻辑回归、神经网络等。
是分类特征处理中的经典方式,本质上也是 One-Hot Encoding 的思想。
4.6.2 连续属性的二值化(对应对比图)

在这张图中,给出了 Aggregation、Sampling、Discretization 和 Binarization 的对比。
其中,关于二值化本身,图中这一句非常关键:
Binarization transforms continuous attributes into binary values based on a threshold.
也就是说:
对连续属性进行二值化时,通常是根据某个阈值(threshold)进行判断:
举个图中的例子:
如果设定温度阈值为 20°C:
温度 ≥ 20 → 记为 1
温度 < 20 → 记为 0
例如:
18°C → 0
21°C → 1
15°C → 0
26°C → 1
这种方式常用于:
风险判断(是否高风险)
是否触发报警
是否达到标准
二分类建模(如是否违约、是否生病等)
可以理解为:
把“连续变化”,压缩为“是否发生”。
4.7 四种预处理方法对比讲解
你最后这张图,是对 四种预处理方法的整体总结对比,这一部分你博客里建议单独写一小节总结,非常加分。
(1)Aggregation(聚合)
Aggregation 的核心是:
把多个数据合并成一个数据
例如:
将每天销售额汇总为每月销售额。
本质是:
改变数据的尺度
减少数据量
降低数据波动
适合:时间序列分析、大规模数据压缩。
(2)Sampling(采样)
Sampling 的核心是:
从大数据集中选取一个具有代表性的小样本集。
比如:
从 100 万条数据中,抽取 5 万条进行初步建模。
目标是:
减少计算成本
保留数据分布的代表性
适合:大规模数据挖掘、初步探索分析。
(3)Discretization(离散化)
Discretization 的核心是:
将连续属性转为有限个区间类别。
例如:
将年龄划分为儿童、成年、老年。
适合:
决策树
规则挖掘
某些分类任务
其特点是保留了类别信息,但降低了精度。
(4)Binarization(二值化)
Binarization 的核心是:
将数据进一步压缩成 0 / 1
例如:
是否高于某阈值、是否属于某类别。
适合:
神经网络
支持向量机
逻辑回归
本质是:
在保留关键信息的同时,极大简化数据表示。
五、Attribute Transformation(属性变换)
5.1 什么是 Attribute Transformation?

根据图中的定义:
An attribute transform is a function that maps the entire set of values of a given attribute to a new set of replacement values such that each old value can be identified with one of the new values.
简单理解就是:
属性变换是一种函数映射,它把一个属性的所有原始取值,转换成一组新的取值。
这个新的取值集合,通常具有以下特点:
更容易参与模型训练
数据尺度更加统一
捕捉更有意义的特征
也就是说,它不是简单“修改”数据,而是通过规则“重构”数据表达方式。
5.2 常见的属性变换函数
你图中列出了几种常见的简单变换函数,包括:
xk:幂次变换
log(x):对数变换
ex:指数变换
∣x∣:绝对值变换
这些函数常用于处理数据分布不均、数值跨度大或存在异常值的情况。
比如:
对数变换常用于压缩右偏分布(如收入数据、访问量等)
幂变换可以放大或缩小数据差异
绝对值常用于消除符号影响
在数据挖掘中,这些变换可以提升模型的稳定性和数值表现。
5.3 Normalization(归一化)
Normalization 属于属性变换中非常重要的一部分,它主要解决不同属性量纲不一致的问题。
图中的解释是:
Refers to various techniques to adjust to differences among attributes in terms of frequency of occurrence, mean, variance, range.
也就是说,归一化的作用是:
缩小不同属性之间的取值差距
使数据落在统一范围内,比如 [0,1]
避免大数值属性“压制”小数值属性
例如:
身高是 150~190,体重是 40~100,直接放进模型会使身高影响过大。
通过归一化可以让它们处于相近尺度。
此外,图中还提到:
Take out unwanted, common signal, e.g., seasonality
说明在时间序列中,属性变换也可以用于去除季节性等重复干扰信号,使数据更加“纯净”。
5.4 Standardization(标准化)
标准化(Standardization):
subtracting off the means and dividing by the standard deviation
也就是经典公式:
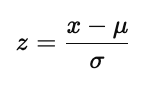
标准化的特点是:
转换后的数据均值为 0
标准差为 1
常用于机器学习算法(如 SVM、KNN、回归等)
相比归一化,它更适合处理接近正态分布的数据。
5.5 温度属性变换案例讲解
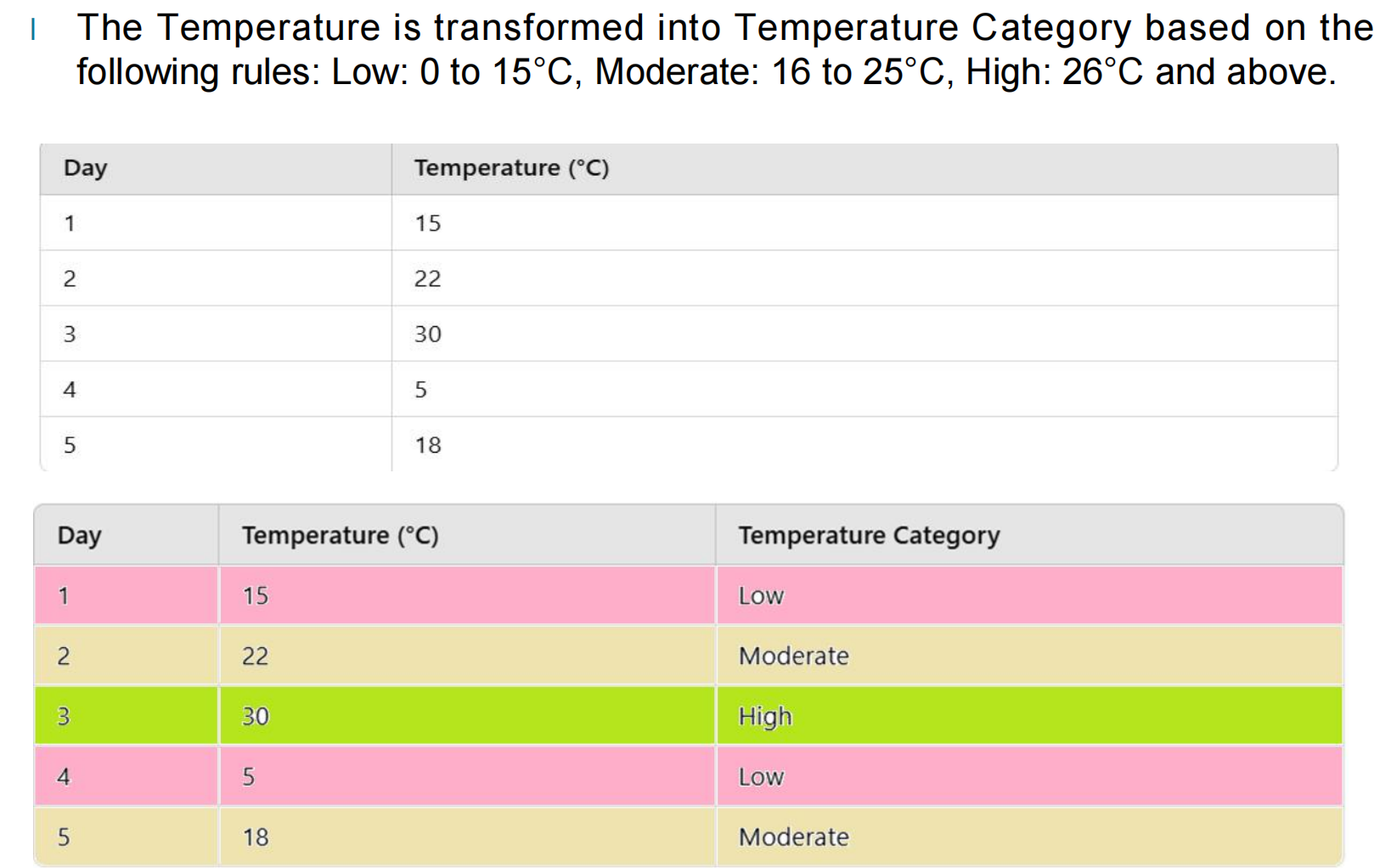
图给出了一个非常清晰的示例,假设我们有如下温度数据:
然后按照规则进行属性变换:
Low:0 – 15°C
Moderate:16 – 25°C
High:26°C 及以上
最终得到:
这个过程本质上就是:
把连续型数值属性 → 变换成离散类别属性
它与离散化有相似之处,但不同点在于:
这里强调的是对“属性含义”的重新编码,而不仅仅是区间划分。
这种方法在天气分析、用户等级划分、风险分级等任务中非常常见。
六、Dimensionality Reduction(降维)
6.1 维度灾难(Curse of Dimensionality)

在高维空间中,数据会变得越来越稀疏(sparse)。当我们从二维过渡到三维、四维甚至更高维度时,样本点之间的“距离”不再像低维空间那样具有直观意义,很多基于距离和密度的方法会逐渐失效。
第一点:
当维度不断增加,数据在整个空间中的分布会变得非常稀疏。比如在二维平面上,点比较容易靠近;但到了几十维甚至上百维时,所有点看起来几乎都是“彼此很远”的,想找到真正的邻居变得非常困难。
第二点:
密度(density)和距离(distance)这两个概念在高维空间中会变得越来越不可靠。比如在聚类(clustering)和异常检测(outlier detection)中,很多算法依赖“点与点之间的距离”来判断相似度,但在高维中,不同样本间距离的差异会变得很小,导致算法难以区分哪些点是近的,哪些是远的。
所以,维度灾难本质上说明一个问题:
➡ 维度越高,传统机器学习算法的效果和计算复杂度都会受到严重影响。
这也正是我们引入“降维”的原因。
6.2 降维的目的(Purpose of Dimensionality Reduction)

结合你图中的内容,降维主要有以下几个学习重点(我帮你解释成课程风格的语言):
避免维度灾难
通过减少特征数量,让数据重新变得“相对密集”,这样更有利于后面的聚类、分类等任务。降低时间和空间复杂度
特征越多,算法计算越慢,占用内存越大。降维可以大大减少数据处理所需的时间和内存。方便可视化
高维数据无法直接画出来,通过降维到2维或3维后,可以用散点图、平面图来可视化分析。减少噪声和无关特征
有些特征信息量很低,甚至只是噪声,降维可以帮助我们去除它们,提高模型的鲁棒性。
技术包括:
PCA(主成分分析)、SVD(奇异值分解)以及一些有监督和非线性方法。
6.3 降维的直观例子:从两个特征到一个特征
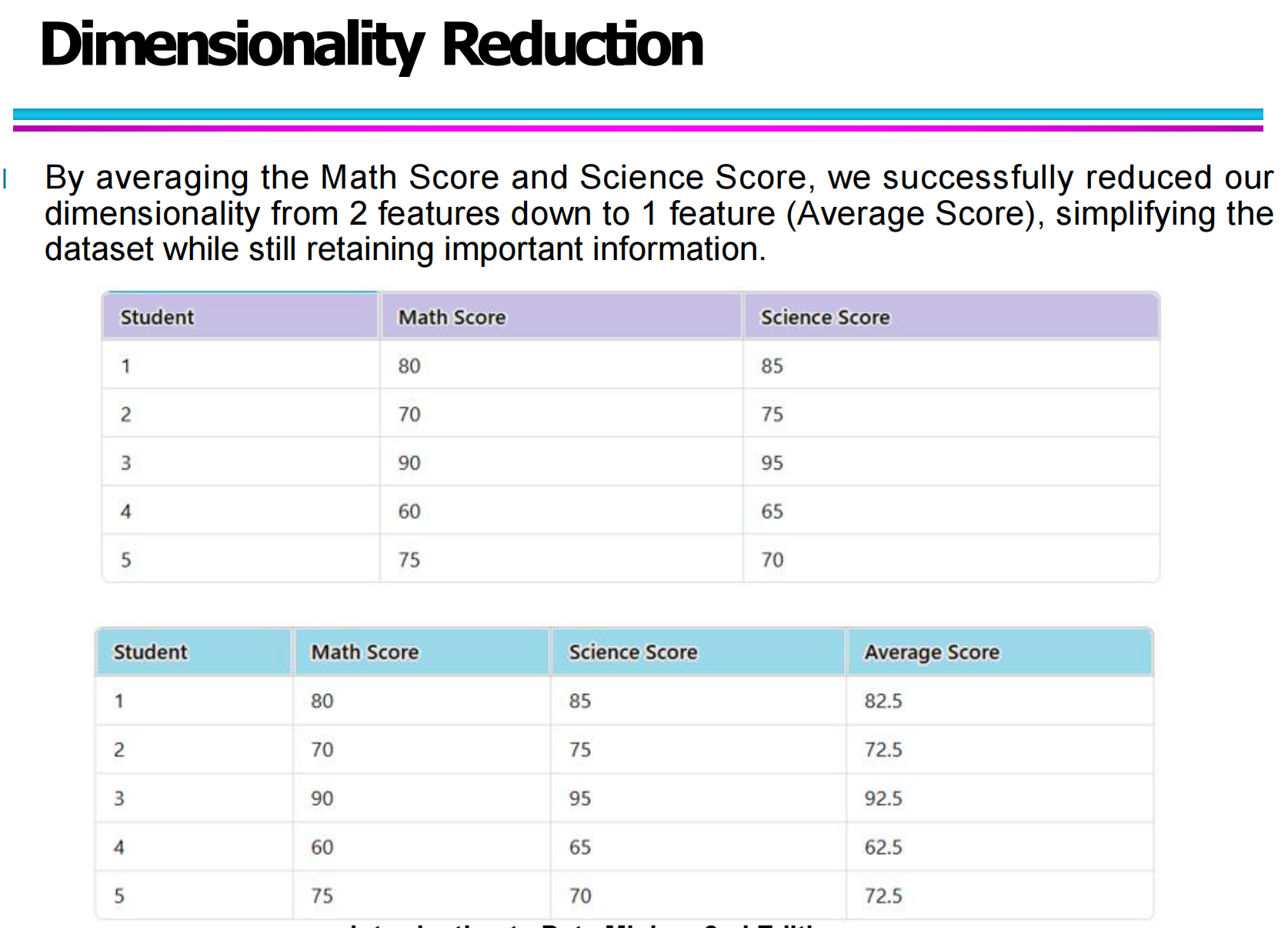
原始数据中,每个学生都有两个特征:
数学成绩(Math Score)
科学成绩(Science Score)
这时,每个学生就是一个二维数据点。
通过计算它们的平均分(Average Score),把两个特征压缩成了一个新特征:
Average=(Math+Science)/ 2
这样,数据维度从 2 维 → 1 维,虽然少了一个维度,但大致仍然保留了学生整体成绩的信息。
这就是一种非常直观的人工降维方式,本质上就是:
用更少的变量,尽可能保留原始数据的主要信息。
这种思路在实际机器学习中特别常见,比如:
多个传感器信号 → 提取一个综合指标
多个学科成绩 → 转换为综合能力评分
多维用户行为 → 压缩成几个兴趣因子
七、Feature Subset Selection(特征子集选择)
7.1 什么是特征子集选择?

在高维数据中,并不是所有特征都是有用的。有些特征可能是冗余的,有些甚至是无关的,这些特征不仅不会提高模型效果,反而可能增加计算负担,甚至降低模型性能。
特征子集选择的目标就是:
从原始特征集合中选出一个更小、更有效的子集,同时尽量保留重要信息。
它本质上也是一种降维方法,但与“特征变换”不同,特征子集选择是直接保留或删除原始特征,而不是对其进行重新组合。
7.2 冗余特征(Redundant Features)
冗余特征指的是:
重复包含了部分或全部其他特征信息的属性。
例如:
商品购买价格(Purchase Price)
缴纳的销售税(Sales Tax Paid)
如果销售税是购买价格的固定比例计算出来的,那么这两个特征之间就高度相关,其中一个可能是冗余的。
冗余特征的问题在于:
增加数据维度
增加模型训练时间
容易导致模型过拟合
因此,在实际建模前通常会先对这类特征进行筛查。
7.3 无关特征(Irrelevant Features)
无关特征是指:
对当前数据挖掘任务没有任何帮助的信息。
例如:
在预测学生 GPA 的任务中,学生的 Student ID 通常是无关特征。
因为学号只是一个标识符,不包含任何学习能力信息。
如果不去除这些特征,可能会:
降低模型泛化能力
干扰特征之间的真实关系
增加模型复杂度和噪声
7.4 特征子集选择的实际示例
原始数据集包含以下特征:
Student ID
Age
GPA
Hours Studied
Purchase Price
Sales Tax Paid
通过分析可以发现:
Student ID:是无关特征
Purchase Price 和 Sales Tax Paid:是冗余特征
Age、GPA、Hours Studied:是相对有用的特征
因此,我们可以将特征子集选择为:
Age、GPA、Hours Studied
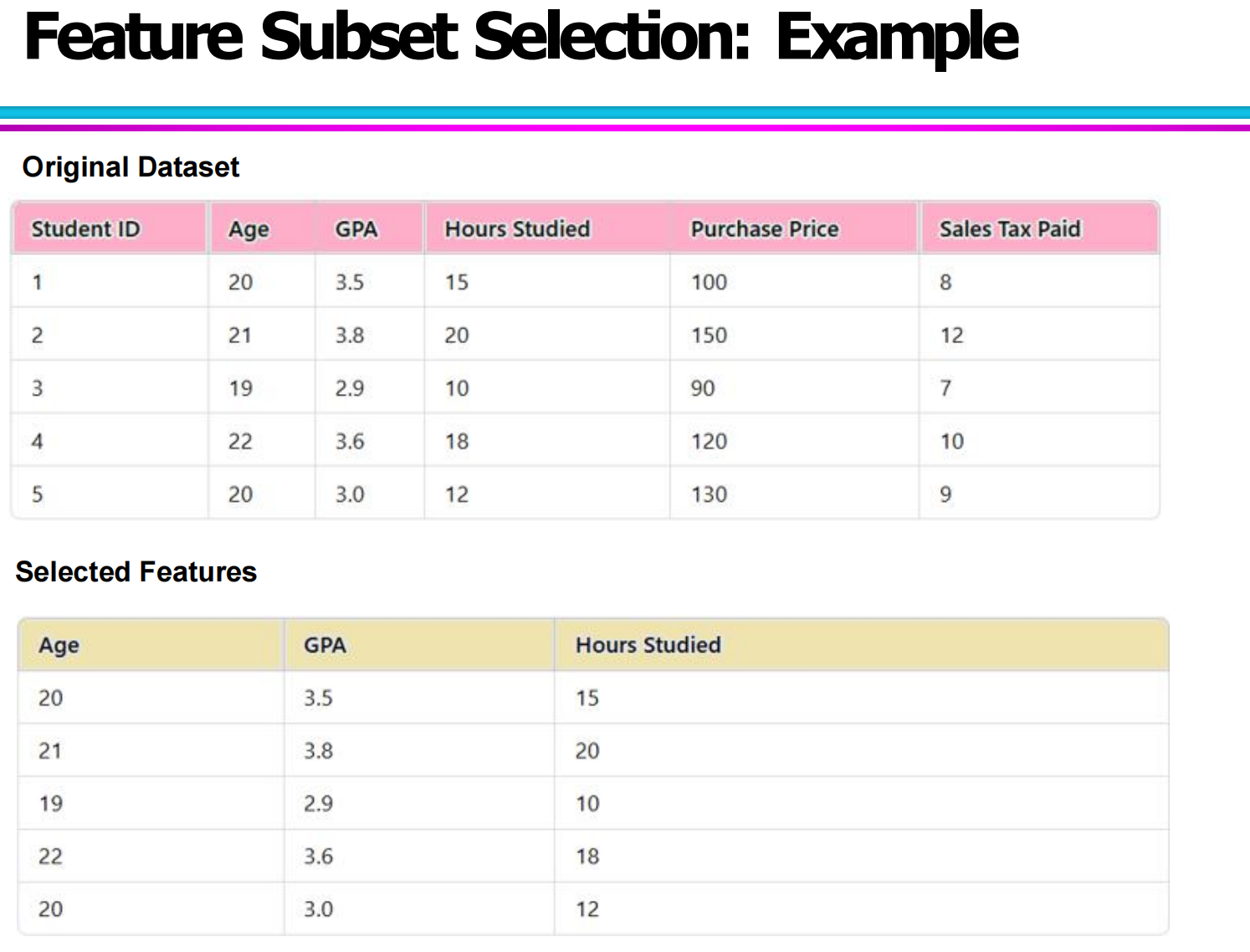
这张图展示了经过特征选择后,保留的有效特征子集,维度从原来的 6 个减少到了 3 个,数据更加简洁,也更利于后续的建模与分析。
7.5 特征子集选择的意义
通过合理的特征选择,可以带来以下好处:
降低数据维度,减少计算成本
提高模型的训练速度
减少噪声干扰,提高模型精度
提高模型的可解释性
这一过程在分类任务中尤其重要,因此目前有很多专门针对分类问题设计的特征选择算法。
八、Feature Creation(特征构造)
8.1 特征创建的基本思想
特征创建的核心目标是:
通过构造新的属性,更有效地表达数据中的关键信息,这些新特征往往比原始特征更有助于模型学习。

图中的这句话是核心观点:
Create new attributes that can capture the important information in a data set much more efficiently than the original attributes.
通俗理解就是:
不是删特征,而是主动创造更聪明的特征。
8.2 三种特征创建的一般方法
可以分为三种方法:
(1)Feature Extraction(特征提取)
这是从原始数据中直接提取出有代表性的特征,例如:
从图像中提取边缘特征
从语音中提取频谱特征
图中例子是:
从图像中提取边缘(extracting edges from images)
这种方法很常见于:
计算机视觉、语音识别等领域。
(2)Feature Construction(特征构造)
特征构造指的是:
通过已有属性的组合,构造出新的属性。
图中的例子非常经典:
质量 ÷ 体积 = 密度
原始数据中没有“密度”,但通过已有数据构造出了一个新特征,这就属于特征构造。
(3)Mapping data to new space(映射到新空间)
这一点在下图中展示得特别清楚:
通过 傅里叶变换(Fourier Transform) 或 小波变换(Wavelet Transform),把数据从时域映射到频域。
8.3 映射到新空间:傅里叶变换示例讲解
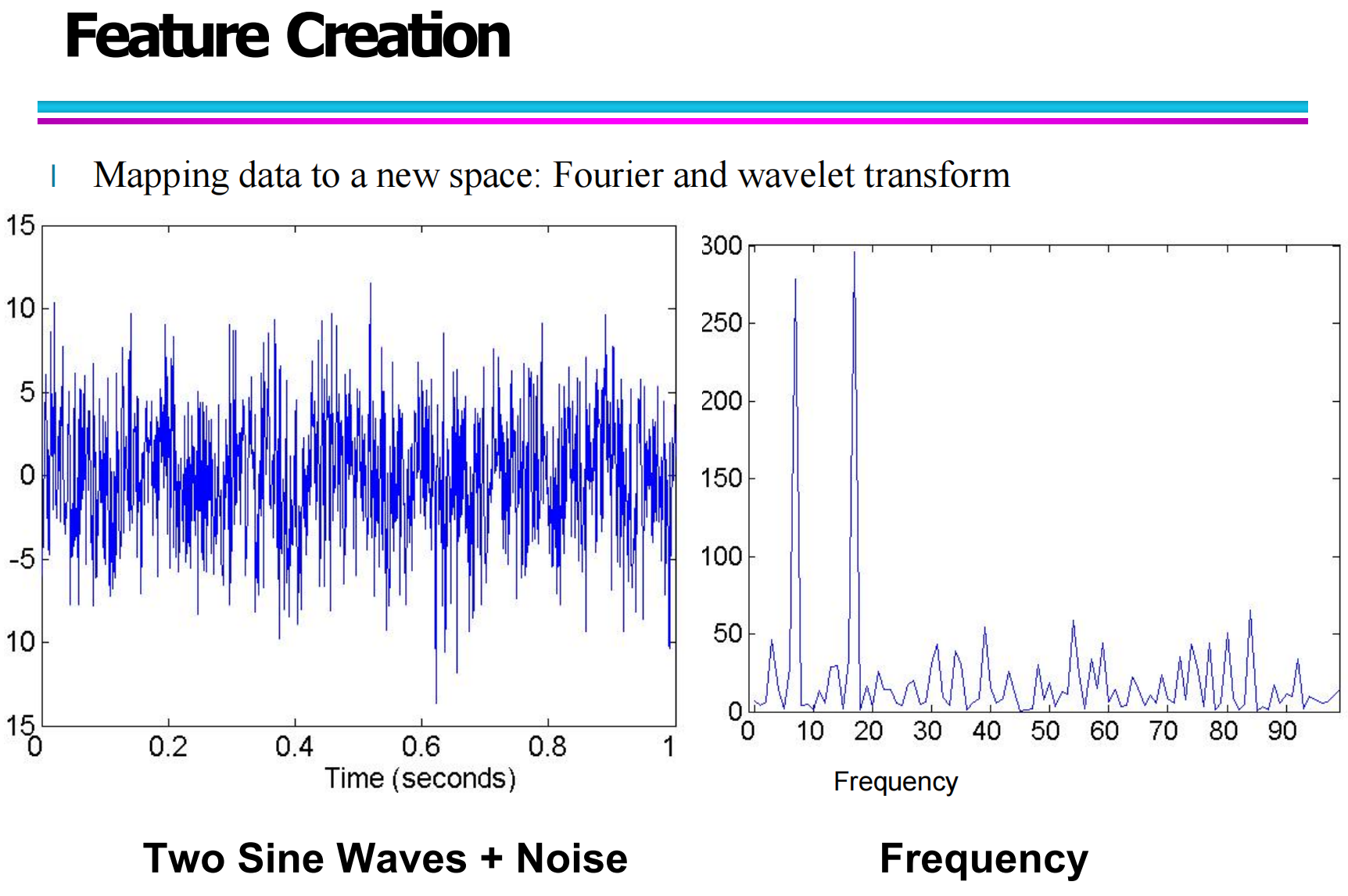
这张图展示了一个非常典型的例子:
左边是:
Two Sine Waves + Noise:
也就是两个正弦波叠加并且带噪声的时域信号。
右边是:
Frequency(频域表示)
通过傅里叶变换之后,信号在不同频率上的能量分布就清楚地显示出来了。
它的意义是:
在时域中,信号杂乱、难以分析
映射到频域后,频率信息变得非常清晰
这相当于为数据创建了一种新的特征表示方式
