一、引言

相关性(Correlation)是数据挖掘和统计分析中最核心的概念之一,它描述了两个或多个变量之间的统计关系。在数据分析过程中,我们经常希望了解数据中的变量是否会同时变化、是否存在某种趋势上的关联,这些信息常常决定后续的建模方向和判断依据。
相关性的重要性体现在,它帮助我们理解数据结构,并揭示潜在的联系。例如,在商业数据中,我们可以利用相关性发现“销量与广告投放量是否同时上升?”,在科研中,我们可能会分析“某种药物剂量是否与病情改善程度有关?”。这些问题的背后,都依赖对变量之间关系的量化描述,而相关性正是其中最常见的手段。
相关性通常用于衡量线性关系的强弱,它能够告诉我们:一个变量增加时,另一个变量是否也会增加(正相关)、是否会减少(负相关),或者二者是否根本不存在关系(零相关)。然而,相关性本身并不代表因果,只能反映变量之间的共同变化趋势,这一点在实际使用中尤为关键。
二、相关性的数学基础

相关性的核心是描述两个变量之间的线性关系到底有多强、方向如何。为了更准确地衡量这种关系,我们通常使用皮尔逊相关系数(Pearson Correlation Coefficient)。这个系数的值介于 –1 到 1 之间,其中 1 表示完全正相关,–1 表示完全负相关,而 0 则代表无线性关系。
皮尔逊相关系数由一个非常直观的数学公式定义,它主要由三部分构成:协方差、x 的标准差、y 的标准差。协方差表示两个变量是否一起变化,而标准差表示变量本身的波动程度。相关系数本质上就是:把两个变量的协方差“标准化”,得到一个范围固定的指标,方便比较。
2.1 协方差(Covariance)
协方差用于衡量两个变量是否倾向于一起变大或变小。
如果两个变量同时增大或减小,协方差为正;
如果一个增大另一个减小,则协方差为负;
如果变化没有明显一致性,则协方差接近 0。
协方差反映了变量关系的“方向”,但它的数值受量纲影响,因此不能直接用于比较。
2.2 标准差(Standard Deviation)
标准差描述一个变量自身的波动情况。
在计算相关性时,需要将协方差除以两个变量各自的标准差,使结果被“缩放”到统一的范围内。
这样一来,无论变量的单位是什么,最后得到的相关系数都在 –1 到 1 之间。
2.3 Pearson 相关系数公式
皮尔逊相关系数是最常用的相关性指标,其公式为:
(图片已在开头指定插入,不再重复)
这个公式告诉我们:相关性由协方差和标准差共同决定,是一个归一化后的线性关系评分。
2.4 一个典型例子:相关性为零不代表没有关系
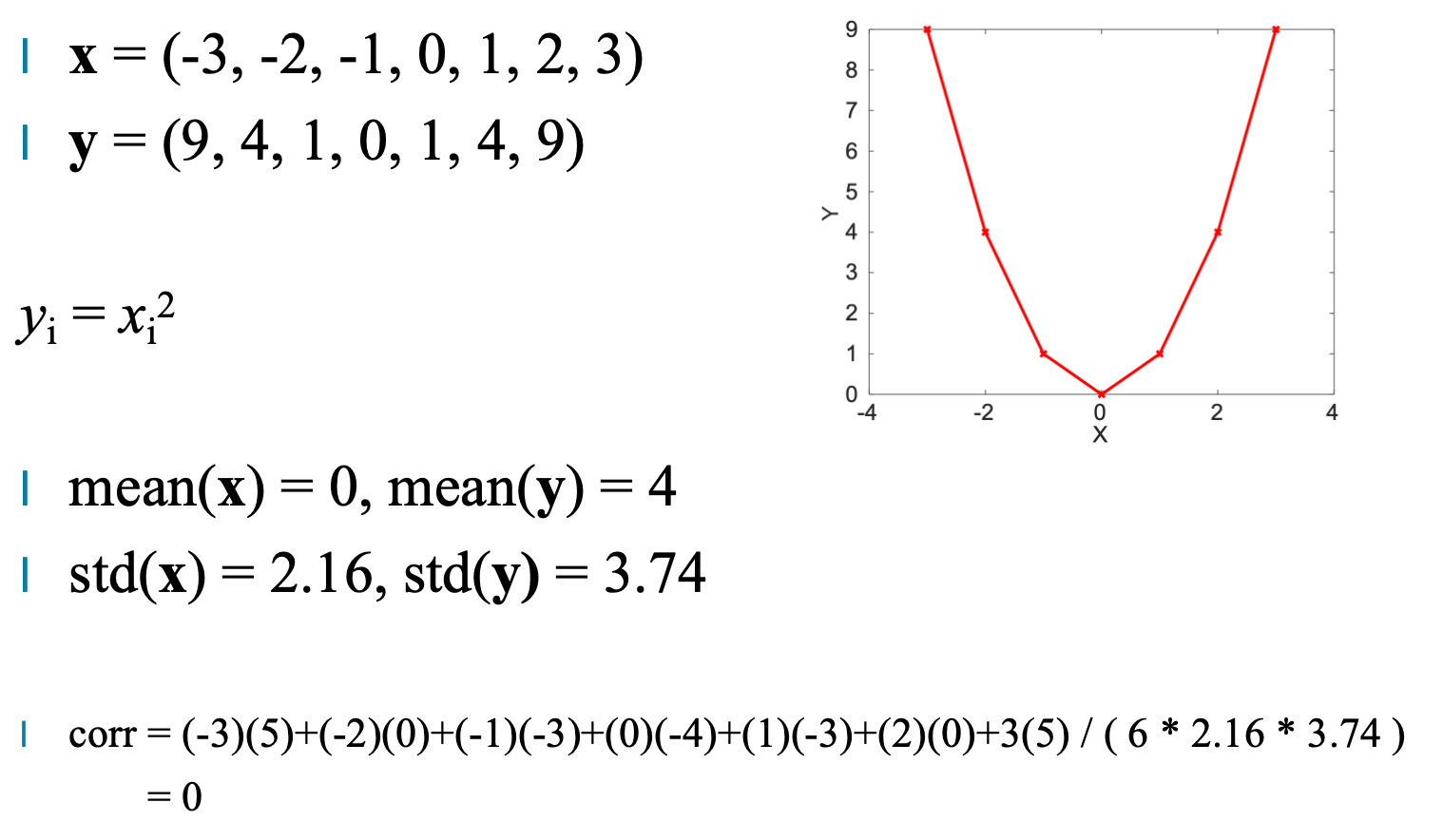
这里有一个经典的例子。
假设:
x = (-3, -2, -1, 0, 1, 2, 3)
y = x² = (9, 4, 1, 0, 1, 4, 9)
虽然 y 完全由 x 计算而来,二者具有非常强的关系,但计算出的 相关系数却是 0。
原因是:
y = x² 是一个对称的非线性关系,并不符合线性规律。
这个例子非常重要,因为它说明:
相关性只能刻画“线性关系”,不能代表“所有关系”
三、相关性的可视化理解
在理解相关性的时候,单纯依赖数字是远远不够的。即使我们知道皮尔逊相关系数可以从 −1 到 +1,但要真正理解“强相关”“弱相关”“无相关”的差异,最有效的方法还是通过散点图(scatter plot)进行可视化。
散点图能够直观展现两个变量之间的关系。你不仅可以看到它们是否呈线性趋势,也可以观察数据是否存在噪声、离群点,甚至还能判断变量之间的关系是否稳定。
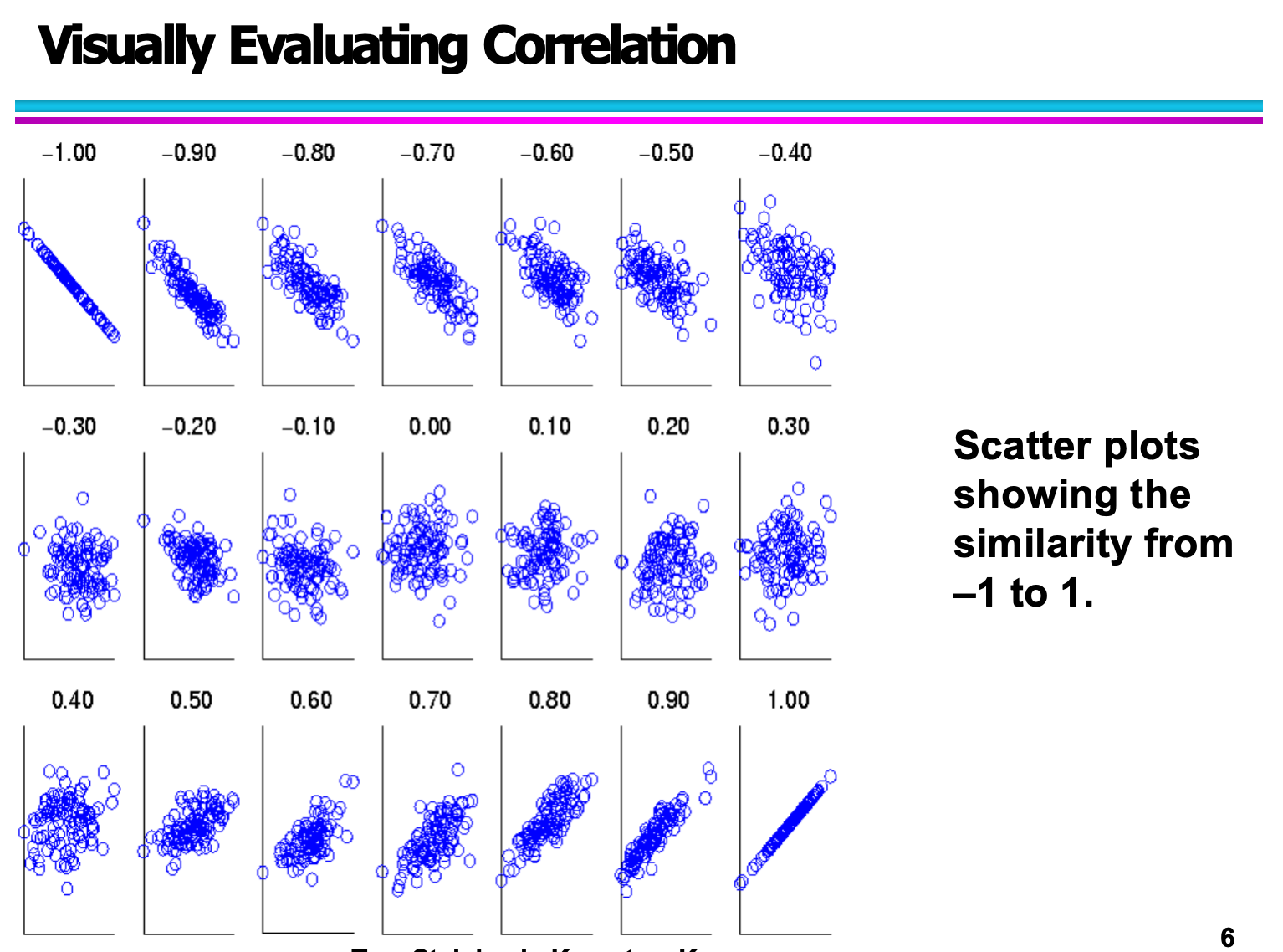
1. 正相关(Positive Correlation)
当一个变量随着另一个变量增大而增大时,它们就是正相关。例如身高与体重、学习时间与成绩之间的关系。散点图中的点通常会沿着左下到右上的方向分布,呈现上升趋势。
如果点分布得非常紧密,趋势清晰 → 强正相关(接近 +1)
如果点大概呈上升趋势但分布松散 → 弱正相关(接近 0 但为正)
从图中可以看到,数据点虽然有一定的波动,但整体呈现一个明显向上倾斜的模式,说明两个变量之间有稳定的正向关系。
2. 负相关(Negative Correlation)
当一个变量随着另一个变量增大而减小时,它们就是负相关。比如运动量增加,体脂率下降;商品价格越高,销量越低等。
散点图会呈现从左上到右下的倾斜方向:
趋势非常明显 → 强负相关(接近 −1)
有下降趋势但不完全一致 → 弱负相关(接近 0 但为负)
图片中的点明显聚集在一条下降斜线上,说明这种变量关系非常典型。
3. 无相关(No Correlation)
没有相关性的两个变量之间没有固定的数学关系,点呈现随机散落,找不到任何线性趋势。
例如学生的学号与成绩之间就没有任何关系。
图中可以看到,散点完全无规律地分布在整个二维空间里,看不出上升或下降的趋势,说明两个变量是完全独立的。
4. 通过趋势判断相关性强弱
这一组图用更直观的方式展示了:
强相关:点紧密贴近一条直线
弱相关:点围绕趋势线松散分布
相关方向:上升为正相关、下降为负相关
这些趋势线图帮助我们理解:“相关性并不是非黑即白”,而是存在不同程度。现实世界的数据通常会有噪声,所以弱相关也是常见情况。
四、相关性的强度与方向
相关系数(r)的数值不仅告诉我们两个变量之间是否存在关系,也揭示了这种关系的强度(strength)与方向(direction)。理解这两个维度,有助于我们在数据分析中更准确地解读变量之间的关联。

4.1 相关性的强度(Strength)
相关性的强度反映了两个变量之间线性关系的紧密程度。
r 接近 1 或 -1:强相关(Strong correlation)
当 r 的绝对值接近 1 时,表示两个变量之间具有非常紧密的线性关系。
例如:r = 0.92 表示高度正相关。r 接近 0:弱相关(Weak correlation)
当 r 的绝对值接近 0 时,两变量之间几乎不存在线性关系。
例如:r = -0.05 表示基本无关联。
可以简单记为:
4.2 相关性的方向(Direction)
相关性的方向由 r 的符号(+ 或 -)决定。
r > 0:正相关(Positive correlation)
表示一个变量增大时,另一个变量也倾向于增大。
例如:身高与体重通常呈正相关。r < 0:负相关(Negative correlation)
表示一个变量增加时,另一个变量倾向于减少。
例如:汽车油量与可行驶距离呈负相关(油量下降,可行驶距离减少)。
方向性告诉我们变量之间的趋势,而强度告诉我们趋势是否明显。
4.3 小结
强度决定“相关性强弱”,方向决定“关联是正还是负”。
r 的数值兼具这两个信息,因此在解释时应同时关注其绝对值与符号。
理解方向与强度的组合,有助于我们在建模、预测或观察数据趋势时做出正确判断。
五、相关性的局限性
在数据分析和数据挖掘中,相关性是一项非常常用的指标,它能帮助我们判断变量之间是否存在统计关系。然而,相关性并不是万能的,它有一些天然的局限性,如果忽视这些问题,可能会导致错误的结论。本章将结合示例图片进一步解释相关性可能带来的误解。

5.1 高相关 ≠ 因果关系
相关性最常见的问题之一,就是人们容易把“相关”误认为“因果”。
即使两个变量之间具有很高的相关系数,也无法说明其中一个一定导致了另一个的发生。
例如:
冰淇淋销量与溺水人数在夏天会同时上升,但显然冰淇淋不会导致溺水。它们的共同原因是“天气变热”,造成了虚假的因果联想。
5.2 相关性只描述线性关系
Pearson 相关系数只反映变量之间的“线性关联”。
如果两个变量存在非线性关系,即使非常强,也可能被判定为“无关”。
举例:
变量 y=x2 明显具有强关联,但 Pearson 相关系数可能接近 0,因为关系是“U 型曲线”,不是线性的。
因此:
相关系数不会捕捉任何非线性模式。
在非线性场景下,需要改用其他方法(如互信息、Spearman rho、Kendall tau 等)。
5.3 偶然相关(Spurious Correlation)
在大型数据集中,特别是包含很多变量时,很容易出现“偶然相关”,也就是两个变量完全无关,但数据恰好呈现相关性。
常见例子:
美国奶酪消费量与人意外缠绕在床单中死亡人数
海盗数量与全球温度变化
这些荒谬的例子说明:
相关性随样本量增大,更容易出现“假相关”。
需要特别注意数据的逻辑来源,不能盲目信任相关系数。
5.4 相关性可能忽略隐藏变量(Confounding Variables)
有时两个变量看似相关,但它们真正的联系是由第三个“未观测到的变量”驱动的,也称为“混淆变量”。
例如:
学生花学习时间与考试成绩呈正相关
但真实原因可能包括:基础水平、自控能力、课程难度等
因此:
仅凭相关性无法得出可靠的因果推断。
