一、引言

在数据分析、机器学习和信息检索中,衡量“相似性”是一项基础而关键的任务。
不同的数据集、不同的特征空间,都需要一种合适的度量方式来判断对象之间的接近程度。最常见的做法是计算距离(Distance),例如欧氏距离或曼哈顿距离。然而,在许多实际场景中,我们更关心的是两个向量的方向是否一致,而非它们在数值上的绝对差距。
这时,余弦相似度(Cosine Similarity)就成为一种更合适的度量方式。
它通过计算两个向量夹角的余弦值,来衡量它们之间的方向相似性。
即便两个向量的长度不同,只要它们在空间中的方向相近,余弦相似度仍然会很高。
例如,在文本分析中,文档常被表示为高维向量(如 TF-IDF 特征)。
此时,文档的字数或篇幅可能差距很大,但如果内容主题一致,它们的向量方向会非常接近。
因此,余弦相似度能有效排除“长度差异”的影响,只关注特征之间的语义一致性。
这种性质使得余弦相似度在高维空间、文本分析以及推荐系统中应用极为广泛。它不仅是距离度量的补充,更是机器学习中理解“相似性”的重要工具。
二、数学定义

余弦相似度(Cosine Similarity)衡量的是两个向量在空间中方向上的相似程度,
其核心思想源自向量夹角的余弦公式。
通过计算向量之间的夹角,可以得到它们在方向上的一致性程度,而这一角度关系与向量的长度无关。
设有两个向量:

余弦相似度的计算公式为:

其中:
A⋅B=∑ni=1AiBi,表示两向量的点积;
∥A∥和 ∥B∥ 分别表示两向量的模长;
分母部分的模长乘积起到“归一化”作用,使得结果只反映方向关系。
余弦相似度的取值范围为 [−1,1][−1,1]:
当 cos(A,B)=1:两向量方向完全相同;
当 cos(A,B)=0:两向量垂直,即完全无关;
当 cos(A,B)=−1:方向完全相反。
在高维空间中,即便两向量的欧氏距离很大,只要它们指向的方向近似一致,余弦相似度仍然会接近 1。
因此,它是衡量方向一致性而非距离接近性的度量方法。
三、计算实例

为了直观理解余弦相似度的计算过程,我们来看一个具体的例子。
假设有两个向量:

我们依次计算它们的点积、模长以及最终的相似度结果。
(1)计算点积

(2)计算模长
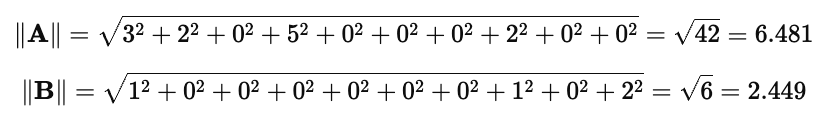
(3)计算余弦相似度

(4)结果分析
计算结果为 0.315,说明两向量的方向略有相似,但整体不完全一致。
在高维空间中,这种“部分相似”的情况非常常见。
例如在文本相似度计算中,尽管两篇文档在用词频率上不同,只要出现了一定的关键词重叠,它们的向量方向仍然会形成较小的夹角,从而得到较高的余弦相似度。
四、计算实例
余弦相似度的核心思想并不是衡量“距离”有多远,而是衡量两个向量之间夹角的大小。
从几何上看,这个夹角直接反映了两个向量在空间中方向是否一致。
设有两个向量:

根据定义:

计算结果表明,两向量夹角的余弦值为 0.28,
这意味着夹角约为 73.7°,两向量方向相差较大,相似度较低。
几何意义解释
当两个向量方向完全一致(夹角为 0°)时,
cos(θ)=1,表示它们“指向同一方向”,相似度最高;当两个向量互相垂直(夹角为 90°)时,
cos(θ)=0,代表它们完全无关;当两个向量方向相反(夹角为 180°)时,
cos(θ)=−1,说明它们方向完全相反。
因此,余弦相似度是一种基于方向一致性的度量,而非基于距离的差异。
图形直观总结
在二维空间中,若两个向量重叠,其夹角接近 0°;
若一个向量顺时针旋转与另一个形成直角,则夹角为 90°;
若旋转至反方向,则夹角接近 180°。
通过这种“夹角视角”,我们可以形象地理解余弦相似度衡量的是向量间的方向相似性。

五、在数据分析中的应用
余弦相似度作为一种衡量“方向一致性”的方法,广泛应用于文本分析、推荐系统、图像识别、异常检测等领域。
它的核心优势在于:即使样本之间的“数量规模”或“幅度”差异较大,
只要它们的变化趋势或特征分布方向一致,余弦相似度依然可以准确捕捉到这种相似性。
1. 文本相似度计算
在自然语言处理(NLP)中,文档往往被表示为高维向量(如 TF-IDF 向量)。
两篇文档即使长度不同,只要词频分布相似,它们的向量方向也会相近。
因此,余弦相似度成为文档聚类、相似内容检测、搜索引擎排名的核心算法。
例如,搜索引擎会计算用户查询向量与文档向量的余弦相似度,
相似度高的文档就被认为与用户输入的查询更“相关”。
2. 推荐系统
在基于内容(Content-Based)的推荐系统中,余弦相似度用于度量物品之间或用户之间的相似性。
例如:
若两部电影在“演员、类型、关键词”等特征上具有相似的特征向量,系统就会判定它们相似;
若两个用户对同一类物品的评分趋势一致,即使评分绝对值不同,系统也会认为他们的兴趣方向相同。
这种“方向相似性”使得推荐算法在面对不同用户评分尺度时依然稳定。
3. 异常检测与特征匹配
在图像处理或行为监测中,余弦相似度可用于判断新样本是否与已有模式方向一致。
例如:
在人脸识别中,通过计算特征嵌入向量之间的余弦相似度,可以判断两张图片是否属于同一人;
在网络安全分析中,余弦相似度用于检测异常流量特征是否与正常行为模式“方向一致”,
从而识别潜在攻击或异常事件。
4. 与其他度量方法的关系
与欧氏距离相比,余弦相似度更关注向量的相对方向而非绝对大小。
因此在高维、稀疏数据场景中(如文本、图像特征、用户行为向量),
余弦相似度往往比欧氏距离更稳定、更鲁棒。
六、总结
余弦相似度是衡量两个向量方向相似性的一种重要方法。
与基于距离的度量(如欧氏距离、闵可夫斯基距离)不同,它忽略了向量的长度和幅度,
而专注于判断它们在高维空间中是否“指向同一个方向”。
这种特性使得余弦相似度在文本分析、推荐系统、图像识别、异常检测等领域具有天然优势,
尤其适用于高维稀疏特征表示。
通过余弦相似度,我们能够:
理解数据之间的“结构性相似”,而不仅是数值差异;
识别特征趋势、语义方向、用户偏好;
为后续的聚类、分类与推荐算法提供更加稳定的相似性度量基础。
未来在深度学习与嵌入表示(embedding representation)的语境下,
余弦相似度仍是连接不同特征空间的重要工具,
无论是在Transformer 模型的语义匹配中,还是向量数据库的相似检索中,
它都扮演着核心的“相似性桥梁”角色。
