一、引言
在机器学习与数据挖掘中,“距离”是衡量两个对象相似度或差异性的重要指标。无论是在聚类(clustering)、最近邻搜索(nearest neighbor search)还是分类任务(classification)中,如何定义“距离”都会直接影响模型的效果。
最常见的距离度量是欧氏距离(Euclidean Distance)和曼哈顿距离(Manhattan Distance)。
然而,它们仅适用于特定场景:欧氏距离强调直线距离,更适合连续型特征;而曼哈顿距离衡量坐标差的绝对值,适合离散或栅格状数据。
为了同时涵盖这两种情形,甚至推广到更高维、更复杂的数据空间,数学家引入了闵可夫斯基距离(Minkowski Distance)。它通过一个可调参数 rr,在不同距离度量之间建立了统一的表达框架,因此被视为一种距离度量的通用形式(generalized distance metric)。
直观理解:
当 r=1 时,它是曼哈顿距离;
当 r=2 时,它是欧氏距离;
当 r→∞ 时,它成为切比雪夫距离。
二、闵可夫斯基距离的定义

闵可夫斯基距离(Minkowski Distance)定义如下:

其中:
x=(x1,x2,...,xn) 与 y=(y1,y2,...,yn) 表示两个 n 维样本向量;
r 为一个可调参数,用于控制不同维度差异的加权方式;
当 r 取不同值时,该距离可退化为多种常见距离度量。
具体而言:
当 r=1:称为 曼哈顿距离(L₁ norm),用于度量坐标轴方向的累积差距。
当 r=2:即 欧氏距离(L₂ norm),用于计算两点间的直线距离。
当 r→∞:称为 切比雪夫距离(L∞ norm),表示各维度差异中的最大值。
这种形式使闵可夫斯基距离成为一种灵活且普适的度量方式,可以通过调整 r 的值适配不同的数据特征与任务需求。
三、参数变化下的实例

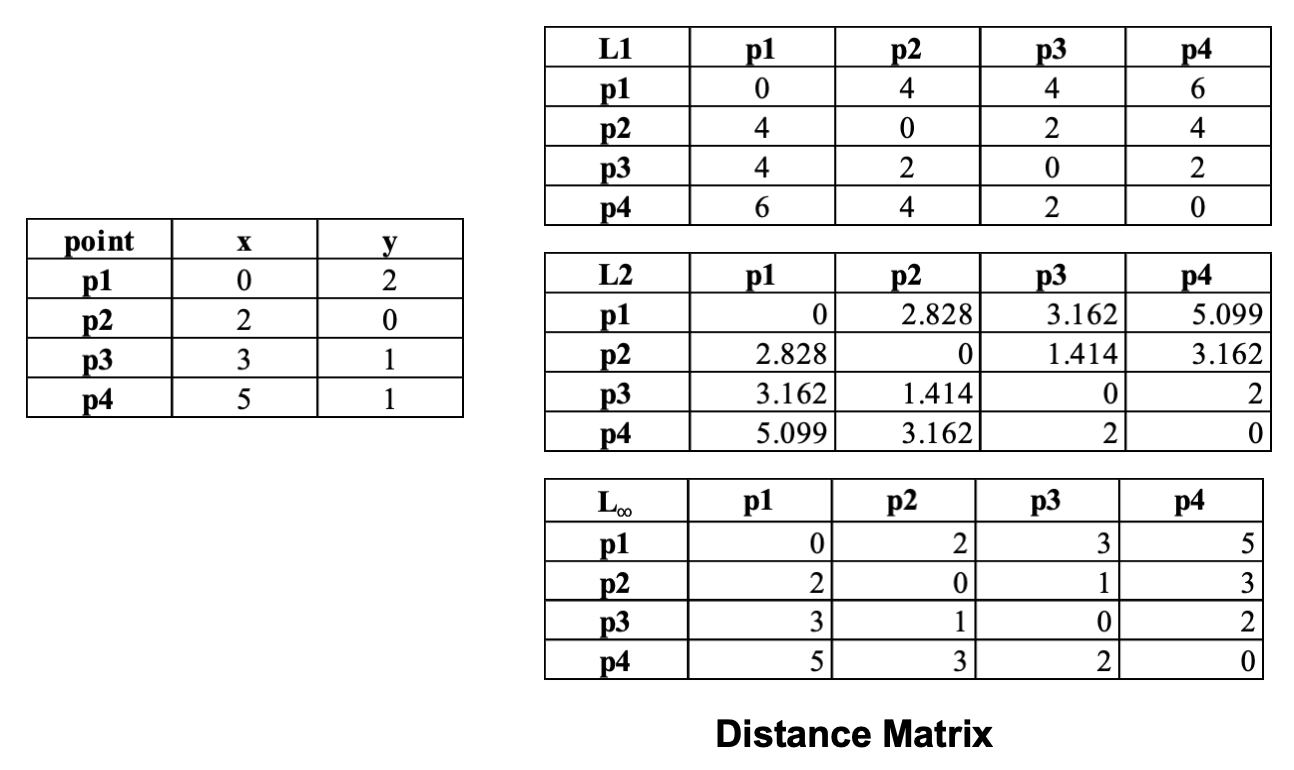
1. 当 r=1:曼哈顿距离(L₁ norm)
此时,闵可夫斯基距离计算各维度差值的绝对值之和,也称为城市街区距离(City Block Distance)。
在几何意义上,它表示在棋盘格上沿水平与垂直方向移动的总步数。
对于二进制向量,一个常见的变体是汉明距离(Hamming Distance),用于统计两个向量在多少个位上不同。
公式为:

2. 当 r=2:欧氏距离(L₂ norm)
当 r=2 时,闵可夫斯基距离退化为欧氏距离,表示两点之间的直线距离。
它是最直观、最常见的距离度量形式,广泛用于几何计算、聚类分析和图像识别中。

3. 当 r→∞:切比雪夫距离(L∞ norm)
当 r 趋于无穷大时,闵可夫斯基距离只考虑各维度中差值最大的那一项。
这种度量方式常用于强调“最坏情况”的偏差,例如在制造或质量检测任务中用于衡量最大误差。
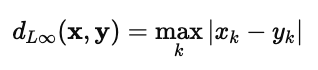
这三种常见情形展示了闵可夫斯基距离在不同应用场景中的多样性:
L₁:更适合离散路径或分段数据;
L₂:用于连续空间下的几何距离;
L∞:用于最大偏差或容忍性分析。
四、不同参数下的计算示例
为了直观理解闵可夫斯基距离如何在不同参数 rr 下表现出差异,
我们以点
x=(1.4,1.6)
与五个样本点的二维坐标为例,计算它们在三种常见范数(L₁、L₂、L∞)下的距离变化。
1. 当 r=2:欧氏距离(Euclidean Distance, L₂ Norm)
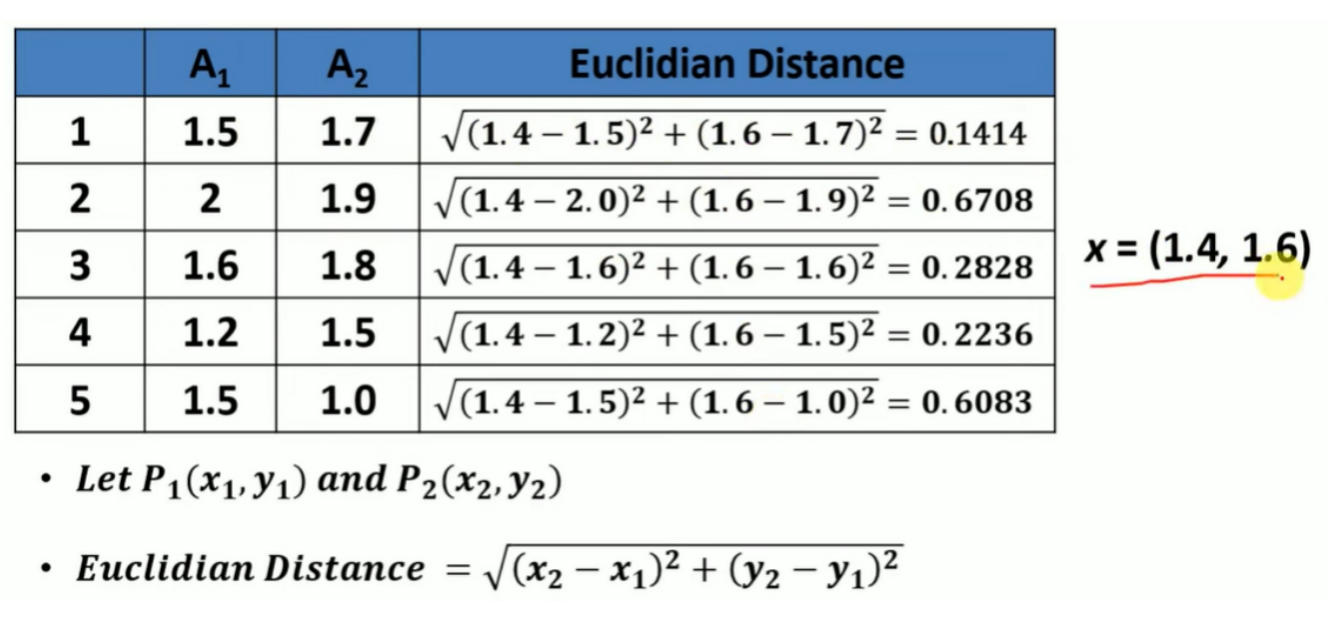
它测量两点间的“直线距离”,考虑了每个维度差异的平方和再开方。

可以看到,A₁ 的距离最小(0.1414),与目标点最为接近。
2. 当 r=1:曼哈顿距离(Manhattan Distance, L₁ Norm)
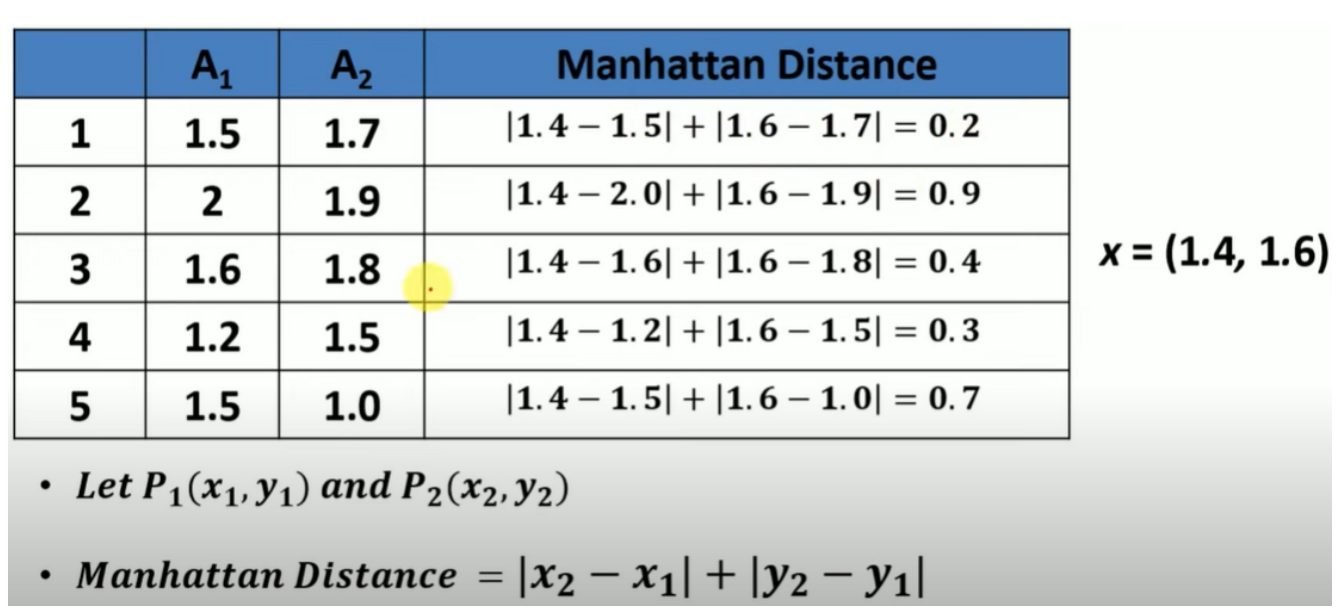
它计算两个点在各维度的绝对差之和,类似沿坐标轴“走格子”的距离。

该度量反映出在不同维度累积偏移的总量。
3. 当 r→∞:切比雪夫距离(Chebyshev or Supremum Distance, L∞ Norm)

在某种意义上,它衡量了“最坏维度”的偏差。
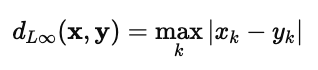
这种距离常用于工业检测或风险评估中,当我们只关心最大误差时尤其有用。
通过对比可以发现:
当 r 较小时(如 L₁),模型更关注整体偏移量;
当 r=2 时,兼顾每个维度的平均差异;
当 r→∞ 时,则聚焦于最大差距维度。
这说明闵可夫斯基距离不仅能统一不同距离度量的数学形式,也为特征空间中的灵活建模提供了理论基础。
五、闵可夫斯基距离与欧氏距离的关系
闵可夫斯基距离(Minkowski Distance)可以被视为一类“广义距离度量”的统一公式,
而欧氏距离(Euclidean Distance)正是其中的一个特例。
1. 数学关系
闵可夫斯基距离的定义为:

当 r=2 时,该公式简化为:

这正是欧氏距离的标准定义。
因此可以认为,欧氏距离是闵可夫斯基距离在参数 r=2 时的特例。
2. 几何解释
在几何空间中,不同的 r 值对应着不同形状的“等距曲线”:
当 r=1 时,等距线是菱形(L₁ 范数对应曼哈顿几何);
当 r=2 时,等距线是圆形(L₂ 范数对应欧几里得几何);
当 r=∞ 时,等距线是正方形(L∞ 范数对应切比雪夫几何)。
这意味着闵可夫斯基距离能够在不同度量标准之间自由切换,
在高维特征空间中调整“距离敏感性”,从而影响模型的聚类或分类结果。
3. 应用视角
在实际应用中:
欧氏距离(r=2):适用于连续特征、平滑空间的聚类(如 K-Means);
曼哈顿距离(r=1):适用于稀疏特征或绝对偏差分析(如 Lasso 回归);
L∞ 距离(r→∞):用于容错性、异常检测等场景。
因此,闵可夫斯基距离不仅是欧氏距离的扩展,更是多尺度相似性度量的统一框架。
