一、梯度下降的含义

梯度下降是一种优化算法，用于通过计算目标函数的梯度（导数）来逐步调整参数，从而最小化损失函数（或最大化收益函数）。

通俗理解：
就像一个人下山，每一步都沿着最陡的方向往下走，最终找到最低点（最优解）。

梯度下降(图1).png

（此J(w，b)并不是平方误差代价函数）

图中提到第一个和第二个谷底都称为局部极小值。
这意味着梯度下降可能会收敛到不同的局部最优解，不一定会全局最优解。（在凸优化问题中可以达到全局最优解）

二、梯度下降算法迭代公式

梯度下降(图2).png

1. 梯度下降的迭代公式

Repeat until convergence（重复直到收敛）：

梯度下降(图3).png

关键点：参数通过减去学习率（α）乘以损失函数 J(w, b) 的偏导数（梯度）来逐步优化。

Simultaneously update w and b（同时更新 w 和 b）：
- 必须使用临时变量（tmp_w, tmp_b）保存新值，再同步更新，避免因顺序更新导致梯度计算错误。

正确代码逻辑：

tmp_w = w - α * ∂J(w,b)/∂w  
tmp_b = b - α * ∂J(w,b)/∂b  
w = tmp_w  
b = tmp_b

错误示例：
- 若先更新 w，再使用新 w 计算 b 的梯度，会导致导数失效（依赖已更新的参数）。

2. 注意事项

强调同步更新的必要性：
- 图中用“不要在右边使用这个不正确的版本”警示错误写法（即分开更新 w 和 b）。
数学符号说明：
- 偏导数（∂J/∂w, ∂J/∂b）代表损失函数对参数的梯度方向。
- := 表示赋值操作（编程中的变量更新）。

三、梯度下降的计算过程以及导数的作用

1. 梯度下降的计算过程

梯度下降(图5).png

2. 导数的作用

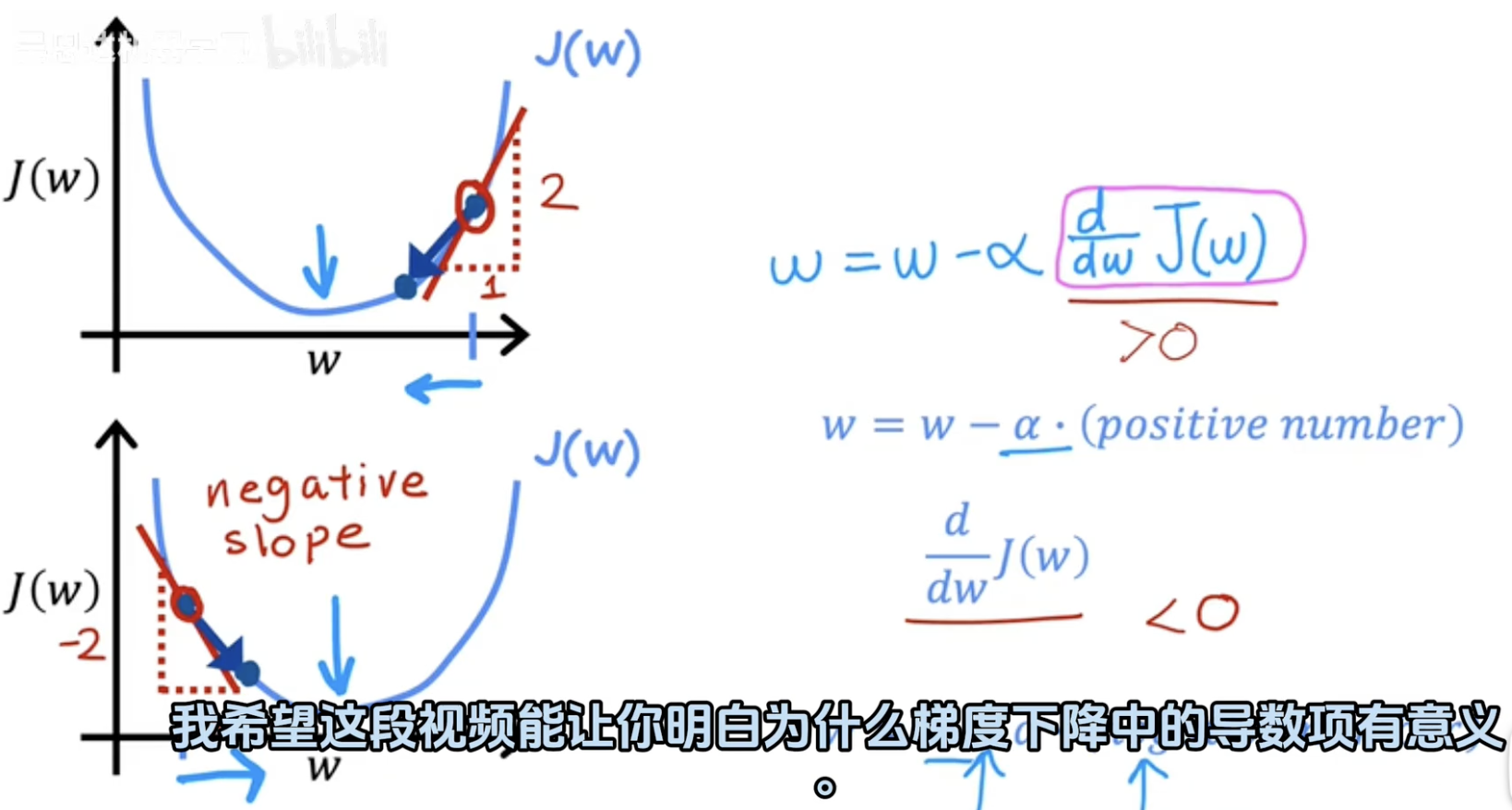
梯度下降(图4).png

导数符号决定方向：
- 若导数为正数（d/dwJ(w)>0）：
  - 更新公式变为 w:=w−α⋅(正数)w:=w−α⋅(正数)，即 w 向左移动（减小）。
- 若导数为负数（d/dwJ(w)<0）：
  - 更新公式变为 w:=w−α⋅(负数)w:=w−α⋅(负数)，即 w 向右移动（增大）。
- 核心作用：导数自动引导参数 w 向损失函数的最小值方向移动。

梯度下降(图6).png

四、批量梯度下降

梯度下降(图7).png

1. 问题背景

假设你是一个房产中介，手上有 47 套房子 的数据，包括：

房屋面积（平方英尺）：比如 2104、1416、1534……
售价（万美元）：比如 40万、23.2万、31.5万……

你想找到一个规律：“房子越大，价格越高”，并用它预测新房价。
这就是 线性回归 的任务——拟合一条最合适的直线来表示房价和面积的关系。

2. Batch Gradient Descent 的作用

目标：调整直线的斜率和截距，让预测尽量接近真实房价。
方法：
- 批量（Batch）：每次计算梯度时，都用 全部 47 条数据（而不是单条或小批量）。
- 梯度下降：根据当前误差，一点点调整直线的斜率和截距，让误差越来越小。

3. 直观理解流程

初始化：随便画一条直线（比如斜率和截距都设为 0）。
计算误差：用当前直线预测 47 套房子的价格，算出所有预测值和真实价格的 平均误差。
调整直线：
- 如果误差太大，就 同时微调斜率和截距（比如斜率增加一点，截距减少一点）。
- 调整的方向和幅度由 学习率（步长）控制。
重复：直到误差不再明显减小，得到最终直线。

4. 为什么叫“Batch”？

“Batch” = 一批：每次更新都用 所有数据（47 条），而不是像随机梯度下降（SGD）那样只用 1 条，或者 Mini-batch 那样用 10 条。
优点：更新方向稳定，不容易乱跳。
缺点：数据量大时（比如 100 万条），每次计算会很慢。

五、验证梯度下降

梯度下降(图8).png

目标：最小化成本函数J(w,b)，确保每次迭代后J(w,b)值都在减小。
学习曲线：展示了J(w,b)随迭代次数的变化趋势。图中横轴是迭代次数（0到400次），纵轴是J(w,b)的值。曲线显示J(w,b)在400次迭代后可能已经收敛。
自动收敛测试：定义了一个阈值ε（epsilon，例如10^-3）。如果在一次迭代中J(w,b)的减小幅度≤ε，就认为算法已经收敛。此时得到的参数w和b已经接近全局最小值。

菜单

Gradient Descent｜梯度下降

分享