一、引言:从熵到互信息的思考

在信息论中,熵(Entropy) 是一个核心概念,它描述了系统中不确定性的程度。通过计算熵,我们可以衡量一个随机变量在平均意义上包含了多少信息量。换句话说,熵越高,代表系统越混乱、越不可预测。
然而,熵只能反映单个随机变量的特性。在现实世界中,我们更关心的是两个变量之间的关系。例如,一个学生的考试成绩是否与他平时的出勤率相关?股票价格是否受到市场情绪的影响?这些问题都超越了单个变量的范围。
于是,互信息(Mutual Information, MI) 的概念应运而生。它用于衡量两个随机变量之间的“信息共享”程度,即:一个变量的取值对另一个变量的不确定性减少了多少。通过互信息,我们能够量化变量之间的依赖关系,从而揭示更深层次的统计规律。
与熵相比,互信息的关注点不在“信息量的多少”,而在“信息如何被两个变量共同持有”。
二、互信息的定义与含义

互信息(Mutual Information, 简称 MI)是信息论中衡量两个随机变量之间依赖程度的重要指标。它定量描述了一个变量中包含多少关于另一个变量的信息。
通俗地说,如果知道了变量 X,我们就能减少对变量 Y 的不确定性;这种“减少的不确定性”就是互信息所刻画的部分。
数学上,互信息可以理解为两个熵之间的差值。
它不仅仅告诉我们“变量之间是否有关联”,还揭示了这种关系的强度与方向。与皮尔逊相关系数不同,互信息不局限于线性关系,它同样能够捕捉复杂的、非线性的依赖模式。
换句话说:
当 I(X,Y)=0 时,表示两个变量相互独立;
当 I(X,Y)>0 时,表示它们存在一定的信息共享;
值越大,变量之间的依赖越强。
因此,互信息在统计学习、信号处理与机器学习领域中被广泛应用,用于特征选择、模式识别、图像配准等任务中。
三、互信息与熵的关系

在信息论中,熵(Entropy) 用于度量一个随机变量的不确定性,而互信息(Mutual Information) 则描述了两个变量之间共享的信息量。换句话说,互信息可以看作是“一个变量对另一个变量的不确定性减少的程度”。
我们可以这样理解它们的关系:
熵 H(X):表示随机变量 X 的不确定性;
联合熵 H(X,Y):表示 X 和 Y 共同的不确定性;
条件熵 H(X∣Y):表示在已知 Y 的情况下,X 还剩多少不确定性。
互信息与这些熵量的关系可通过以下公式体现:
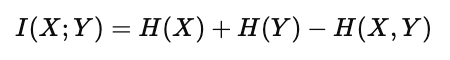
这一定义揭示了一个关键事实:
互信息是单个变量的不确定性与联合不确定性之间的差值。
也就是说,当两个变量完全独立时,H(X,Y)=H(X)+H(Y),因此 I(X;Y)=0I(X;Y)=0;而当两个变量完全相关时,联合熵等于单个熵,互信息达到最大。
四、互信息的数学表达式与推导
互信息不仅是一个概念性指标,更是一个可计算的数学量。它的核心思想是:通过比较两个变量的联合概率分布与各自独立概率分布的差异,来衡量它们之间的依赖关系。
1. 互信息的定义式
互信息的标准定义为:
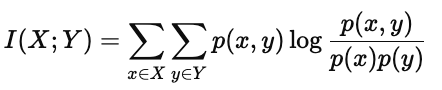
其中:
p(x,y):表示 X 与 Y 的联合概率分布;
p(x)p(y):表示在独立假设下,两者的乘积分布;
对数项 :衡量实际分布与独立分布之间的偏离程度。
如果 X 与 Y 完全独立,则 p(x,y)=p(x)p(y),从而 I(X;Y)=0。
这表明:互信息越大,代表它们之间的依赖关系越强;反之越小,则越接近独立。

2. 与熵的关系再表达
互信息也可以用熵的形式重写为:
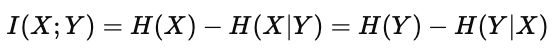
这说明互信息本质上就是已知一个变量后另一个变量的不确定性减少量。
它体现了两个变量之间“信息共享”的对称性:
无论是从 X 到 Y,还是从 Y 到 X,结果都是相同的。
五、互信息的实例计算与理解
理论定义清晰之后,我们来看一个具体的互信息计算实例。这个例子展示了如何通过熵的概念来量化两个变量之间的信息依赖程度。
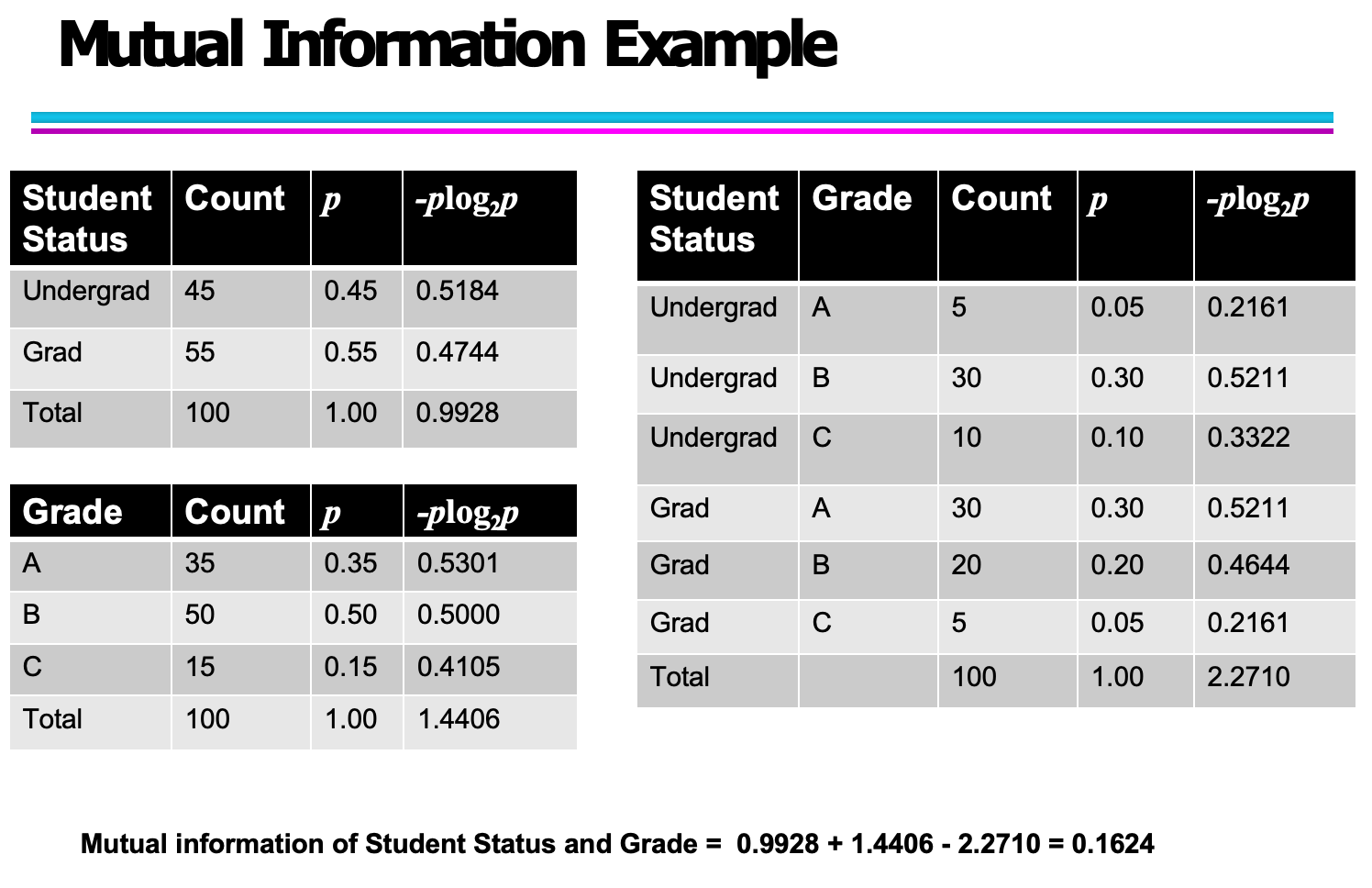
1. 数据背景
我们有两个变量:
Student Status(学生身份):本科生(Undergrad)与研究生(Grad);
Grade(成绩等级):A、B、C 三个等级。
目标是计算这两个变量之间的互信息(Mutual Information, MI),即学生身份与成绩之间共享的信息量。
2. 熵的计算过程
(1)首先,计算每个变量自身的熵:
学生身份熵:
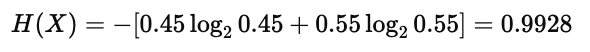
成绩等级熵:
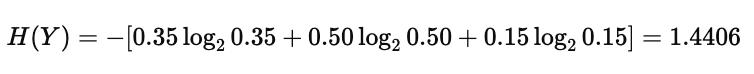
这两个值分别反映了学生身份和成绩等级本身的不确定性。
(2)然后,计算它们的联合熵:
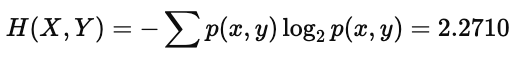
该值体现了当我们考虑两者联合分布时系统整体的不确定性。
3. 互信息的求解
根据公式:
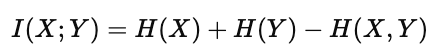
代入上面的计算结果:
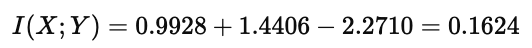
由此得到互信息为 0.1624 bits。
4. 结果分析
这个数值较小,说明“学生身份”和“成绩等级”之间的依赖关系较弱。
换句话说,知道一个学生是本科生还是研究生,对预测他(她)拿到A、B或C的成绩帮助并不大。
在信息论的意义上,这表明两个变量之间的“信息共享”不多,系统中仍存在较大的不确定性。
六、互信息的应用与总结
互信息(Mutual Information, MI)作为信息论的重要概念,不仅仅是一个数学指标,更是一种在多个领域中都极具价值的分析工具。它通过度量两个变量间的信息共享程度,为数据建模、特征提取和模式识别提供了强有力的理论支撑。
1. 在特征选择中的应用
在机器学习中,特征选择(Feature Selection)是提升模型性能的重要步骤。
互信息可以用来评估某个输入特征与目标变量之间的依赖关系。如果一个特征与目标变量具有较高的互信息值,说明该特征提供了更多有用信息,因此在模型训练中应当保留。
例如,在文本分类任务中,互信息可用来筛选与分类结果最相关的词语,从而减少冗余特征、提升计算效率。
2. 在图像配准与信号处理中的应用
在医学影像、计算机视觉和信号处理领域,互信息被广泛用于图像配准(Image Registration)。
当我们需要对齐两张不同模态的图像(如 CT 与 MRI)时,互信息可以衡量图像间的像素分布依赖程度。
最大化互信息的匹配方式,往往能找到最佳配准位置。
这一原理同样适用于语音信号分析、时间序列比对等场景。
3. 在生物信息学中的应用
在基因组研究中,互信息可用于衡量基因表达模式之间的依赖性。
如果两个基因的表达值变化具有较高的互信息,则它们可能存在某种生物学调控关系。
这种方法帮助研究者在大规模数据中识别出关键的基因网络结构。
4. 理论总结
通过前几章的推导和示例,我们可以总结出以下几点认识:
熵衡量单个变量的不确定性;
联合熵衡量多个变量共同的不确定性;
互信息则揭示了变量之间的依赖程度,即一个变量对另一个变量“揭示”了多少信息。
互信息不仅体现了“相关性”的本质,更在理论上拓展了我们对信息传播与统计依赖的理解。
5. 结语
从熵到互信息,信息论为我们提供了一种新的思维方式,让我们能从概率与不确定性的角度理解数据世界。
无论是人工智能、通信工程,还是生物信息与经济建模,互信息都在不断发挥着基础性作用。
它不仅是数学的产物,更是连接自然界、技术系统与智能认知的“信息桥梁”。
