一、欧式距离定义

欧氏距离（Euclidean Distance）是最常见、最直观的距离度量方法，用于衡量两个点在空间中的“直线距离”。
它可以理解为在 n 维空间中，连接两点的最短路径长度。

数学定义如下：

这里 x_k 和 y_k 分别是点 x 与 y 在第 k 个维度上的坐标。
该公式来源于勾股定理，是二维空间“直角三角形斜边”长度的推广。

通俗理解

如果你在地图上测量两地的直线距离，而不考虑地形、道路等曲折因素，
那么你测到的就是欧氏距离。
比如两个点 A(2,3) 与 B(5,7)，
它们之间的距离为：

欧氏距离越小，两个点越“接近”；越大，差异越明显。

欧氏距离属于“差异度量”

与“相似度量（similarity measure）”不同，
欧氏距离越大代表差异越大，
因此常用于分类、聚类等算法中，帮助我们“区分”不同对象。

二、几何直观

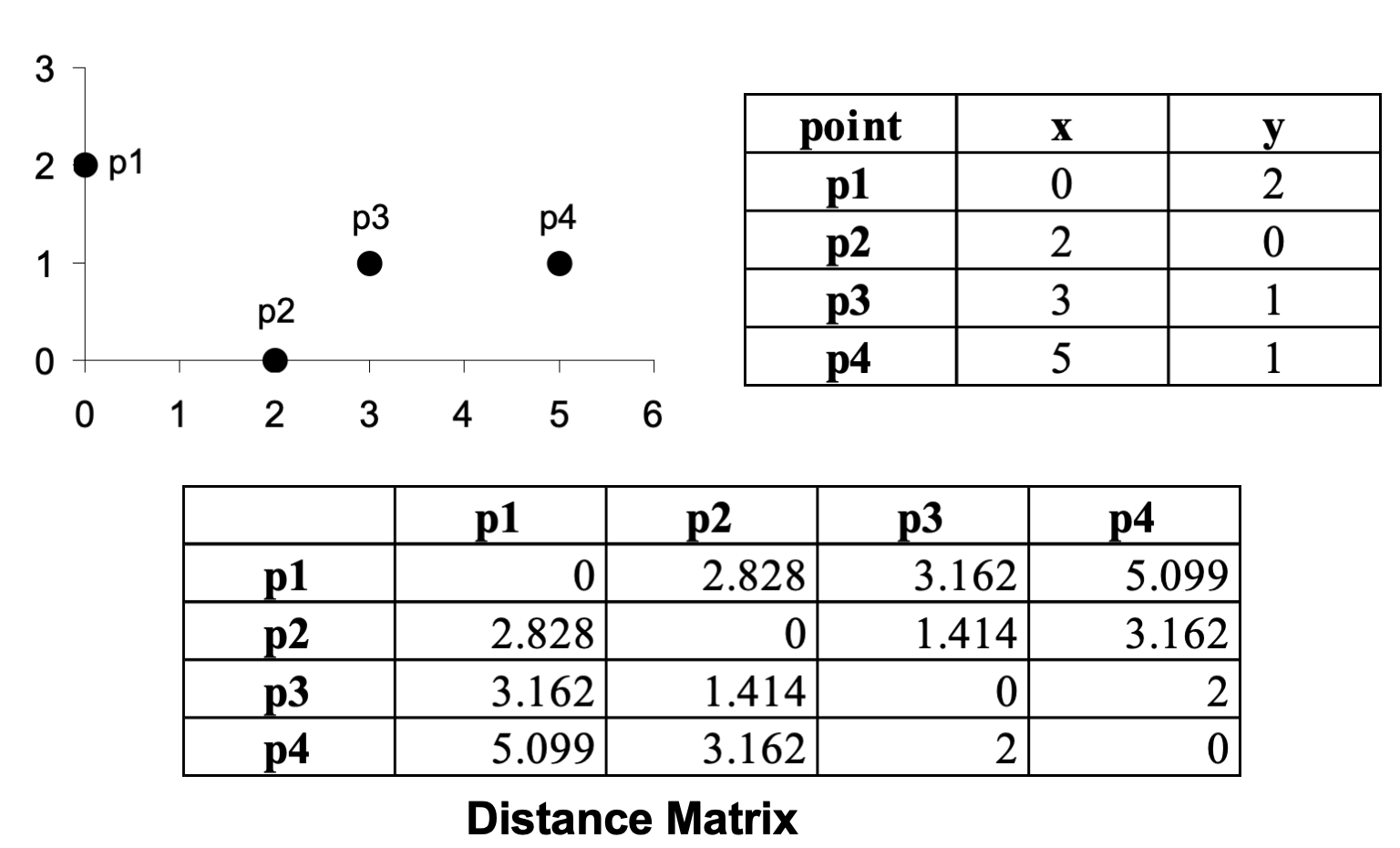
在二维平面上，假设有两个点：

那么它们的欧氏距离为：

从几何角度看，这个公式正是由勾股定理推导而来：

x₂−x₁表示在 x 轴上的水平差距；
y₂−y₁ 表示在 y 轴上的垂直差距；
将这两条边视作直角三角形的两条直角边，
斜边长度即为两点间的最短距离，也就是欧氏距离。

在三维空间中，欧氏距离扩展为：

同理，在 n 维空间中，只需在根号内继续累加各维度的平方差。

直观理解

在二维平面上，以某个点为中心、距离为常数 rr 时，
所有与该点距离相等的点构成一个圆；
在三维空间中则是一个球面。
这说明欧氏距离是各方向等权、对称的。

三、实例计算

在理解了欧氏距离的几何意义后，我们来看一个更贴近数据分析实践的计算示例。
表中展示了一个点 x=(1.4,1.6) 与多个数据点 A_i 之间的欧氏距离计算结果。
每个样本 AiAi 都由两个维度组成（A₁ 和 A₂），代表二维空间中的坐标点。

欧氏距离的计算公式为：

例如，对于第一个点 A₁=(1.5,1.7)：

依此类推，我们可以计算出与每个样本的距离。
这些距离反映了目标点 (1.4,1.6) 与不同数据点之间的相似程度——
距离越小，表示两个样本越接近，也越相似。

分析与应用

距离最小即最相似：从表中可见，第一个点距离最小（0.1414），
因此 A1 是与 x 最相似的样本。
在分类问题中的意义：在 K-近邻算法（KNN）等模型中，
这种“距离最小原则”常被用来判断未知样本的类别。
可扩展到高维空间：虽然这里展示的是二维示例，
但公式可以轻松推广到 n 维，计算方式保持一致。

四、实际应用与思考

在数据科学与机器学习的实际场景中，欧氏距离被广泛用于衡量样本间的相似度。
然而，在真正应用时，我们必须考虑到数据的特征分布、量纲差异与噪声影响。

1. 标准化的重要性

欧氏距离对特征的尺度（scale）十分敏感。
例如，若一个特征以“厘米”为单位，而另一个特征以“万元”为单位，
则后者的数值范围更大，会在距离计算中占据主导地位。

为避免这种偏差，常见的解决方式包括：

Min-Max 归一化：将每个特征线性压缩到 [0, 1] 区间；
Z-score 标准化：将特征调整为均值为 0、方差为 1 的分布。

经过标准化后的欧氏距离能更公平地反映各维度的差异。

2. 高维数据的挑战

在高维空间（例如 100 个以上的特征）中，欧氏距离容易出现“距离集中”问题：
不同样本之间的距离差异变得极小，导致相似度判定失效。
这种现象被称为 “维度灾难（Curse of Dimensionality）”。

解决思路包括：

使用主成分分析（PCA） 降维，提取主要特征；
采用加权欧氏距离，为不同特征赋予不同的重要性权重。

3. 欧氏距离的典型应用

欧氏距离的思想简洁且直观，因此在多个算法中都扮演着核心角色：

K-近邻算法（KNN）：通过计算测试样本与训练样本的欧氏距离来分类。
K-Means 聚类：利用欧氏距离判断样本与聚类中心的相似度。
异常检测（Outlier Detection）：距离过大的点被视为潜在异常值。

这些算法的共同点在于：以空间几何的角度度量样本间的关系，
而欧氏距离正是这种度量的最自然表达方式。

菜单

Euclidean Distance｜欧式距离

分享