一、模型评估的定义
模型评估是衡量机器学习模型性能的关键步骤,通过量化指标(如准确率、召回率等)判断模型是否达到预期目标。它帮助我们发现过拟合、欠拟合等问题,并指导模型优化方向。
通俗理解:
就像考试评分一样——模型评估就是给AI模型“打分”,看看它做题(预测)的正确率有多高,哪些题型(数据)容易错,从而决定是否需要“补课”(调整模型)。

这张图片的标题是 “Debugging a learning algorithm”,内容围绕正则化线性回归模型在房价预测中出现较大误差时的调试方法。
核心点解析:
问题背景:使用带正则化的线性回归(损失函数含L2惩罚项),但预测误差较大。
调试选项:
数据层面:增加样本、减少/增加特征、引入多项式特征。
正则化调整:增大或减小超参数 λλ 以平衡拟合与过拟合。
选项直接对应机器学习中高偏差(欠拟合)与高方差(过拟合)的典型解决策略。
二、机器学习诊断

这张图片的标题是 “Machine learning diagnostic”,内容定义了机器学习诊断的概念。
核心点解析:
诊断定义:一种用于分析学习算法哪些部分有效/无效的测试方法,目的是获取改进性能的指导方向。
特点:诊断可能需要时间实现,但对算法优化是高效的投资。
该定义强调诊断的核心价值是针对性发现问题,而非盲目调整。
三、评估模型

这张图片主要展示了机器学习模型评估中的一个关键问题 - 过拟合(overfitting)现象,并给出了一个房价预测的具体案例。我将从以下几个方面进行详细讲解:
模型结构
展示了一个多项式回归模型:fw,b(x⃗) = w₁x + w₂x² + ... + wₙxⁿ + b
这是一个典型的线性回归的扩展形式,通过引入高次项(x², x³等)来增加模型复杂度
过拟合问题
明确指出该模型"在训练数据上表现良好,但无法泛化到训练集之外的新样本"
这是过拟合的经典定义:模型过度记忆了训练数据的细节和噪声,导致在新数据上表现不佳
房价预测特征
列出了4个典型的房屋特征:
x₁ = 面积(平方英尺)
x₂ = 卧室数量
x₃ = 楼层数
x₄ = 房龄(年)这些特征的选择反映了实际预测任务中常见的结构化数据
潜在问题
模型可能因多项式阶数过高(如xⁿ中n太大)导致过拟合
也可能因特征选择不当或缺乏正则化而导致泛化能力差
1. 划分数据集

这张图片主要展示了用于模型评估的数据集划分情况。以下是核心内容解析:
数据集内容
展示了一个房价预测数据集,包含10条样本
每行数据包含两个特征:房屋面积(size)和价格(price)
示例数据范围:面积1380-3000平方英尺,价格199-540单位
数据划分
明确将数据分为训练集和测试集
训练集:包含7个样本,表示为(x⁽¹⁾,y⁽¹⁾)到(x⁽ᵐ⁾,y⁽ᵐ⁾)
测试集:包含3个样本,表示为(x_test⁽¹⁾,y_test⁽¹⁾)到(x_test⁽ᵐ⁾,y_test⁽ᵐ⁾)
数学表示
使用m_train表示训练样本数量(m_train=7)
使用m_test表示测试样本数量(m_test=3)
采用标准机器学习数据表示法(x⁽ⁱ⁾,y⁽ⁱ⁾)
评估意义
展示了模型评估前的标准数据准备流程
体现了将原始数据划分为训练集和测试集的标准做法
为后续模型训练和评估提供了数据基础
2. 训练/测试
1)线性回归的训练/测试过程

这张图片详细描述了线性回归模型的训练和测试过程,特别是使用平方误差作为成本函数的情况。以下是对图片中每个部分的详细解释:
1. 拟合参数
目标:通过最小化成本函数 J(w,b) 来找到最佳的参数 w(权重向量)和 b(偏置)。
成本函数:
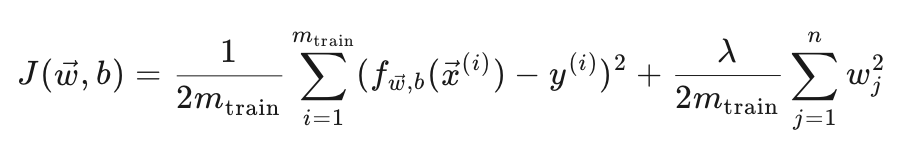
第一部分是训练集上的平方误差,衡量模型预测值与实际值之间的差异。
第二部分是正则化项,用于防止过拟合,其中 λ 是正则化参数,n 是特征的数量。
2. 计算测试误差
目标:评估模型在未见过的数据(测试集)上的表现。
测试误差公式:
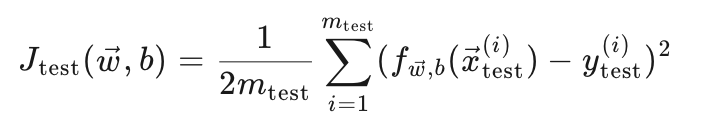
这里计算的是模型在测试集上的平方误差。
3. 计算训练误差
目标:评估模型在训练数据上的表现。
训练误差公式:
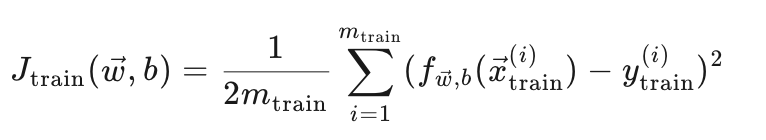
这里计算的是模型在训练集上的平方误差。
这些步骤共同构成了线性回归模型的训练和评估过程,通过最小化成本函数来优化模型参数,并使用训练误差和测试误差来评估模型的性能。
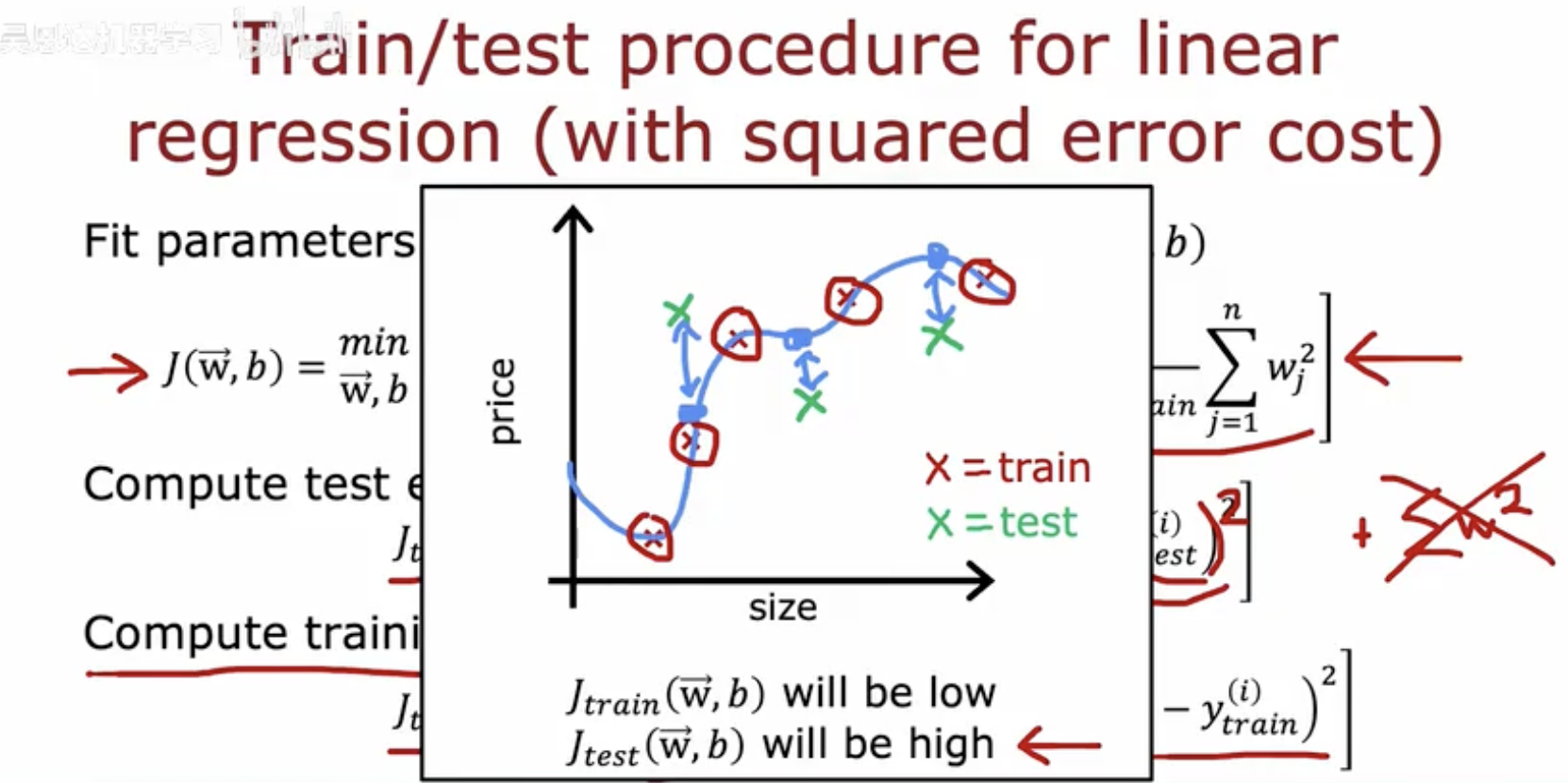
图中还包含一个散点图,展示了训练数据(X)和测试数据(O)的分布,以及拟合的线性回归模型。图中指出,训练误差 Jtrain(w,b) 会较低,而测试误差 Jtest(w,b) 会较高,这可能表明模型过拟合。
2)分类问题的训练/测试过程

这张图片详细描述了分类问题中使用对数损失函数(也称为交叉熵损失)和L2正则化的训练和测试过程。
1. 拟合参数
目标:通过最小化成本函数 J(w,b) 来找到最佳的参数 w(权重向量)和 b(偏置)。
成本函数:
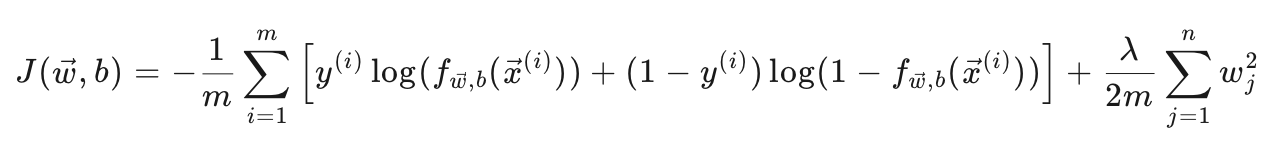
第一部分是交叉熵损失,衡量模型预测概率与实际标签之间的差异。
第二部分是L2正则化项,用于防止过拟合,其中 λ 是正则化参数,n 是特征的数量。
2. 计算测试误差
目标:评估模型在未见过的数据(测试集)上的表现。
测试误差公式:
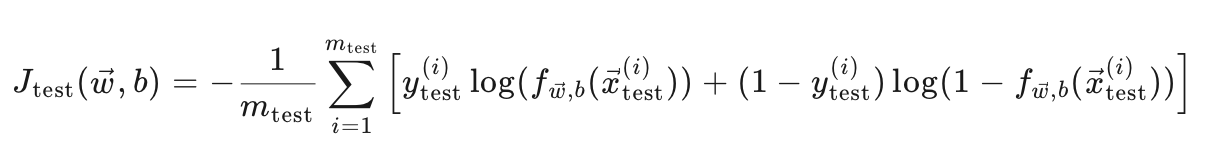
这里计算的是模型在测试集上的交叉熵损失。
3. 计算训练误差
目标:评估模型在训练数据上的表现。
训练误差公式:
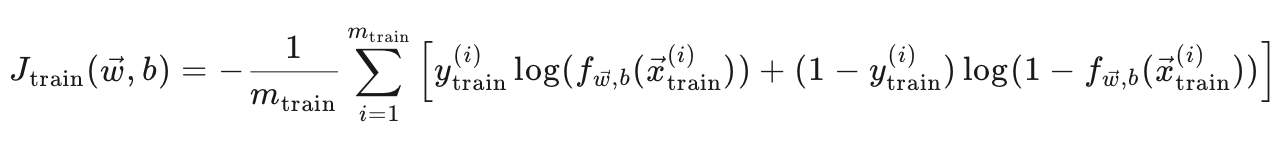
这里计算的是模型在训练集上的交叉熵损失。
这些步骤共同构成了分类模型的训练和评估过程,通过最小化成本函数来优化模型参数,并使用训练误差和测试误差来评估模型的性能。正则化项有助于提高模型的泛化能力,减少过拟合的风险。

图片右侧的注释解释了误差计算中 y^ 的定义,即如果模型预测的概率 fw,b(x(i)) 大于或等于0.5,则 y^=1;否则 y^=0。这些误差计算反映了模型在训练集和测试集上的分类错误比例。
