一、梯度下降的数学公式与直观理解

在机器学习里，我们通过最小化损失函数 J(w,b)J(w,b) 来找到最优参数。梯度下降的核心公式是：

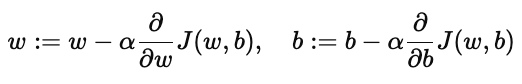
其中：

• α 表示 学习率（Learning Rate），决定了每一步更新的幅度；

• ∂/(∂_wJ(w,b))、∂/(∂_bJ(w,b)) 表示损失函数对参数的导数，也就是梯度。

从直观图像来看（对应第一张图右侧的抛物线）：

• 横轴是参数 w，纵轴是损失函数 J(w)。

• 梯度下降的过程，就是不断从当前位置往下走，每次按照“最陡下降”的方向更新参数。

• 当走到谷底时，梯度为 0，说明达到了最优解。

通俗理解：
就像一个人在山坡上想要走到最低点，他会选择沿着最陡的方向一步步走下去。如果步子太大（学习率过高），可能会跳过谷底；如果步子太小（学习率过低），虽然不会走过头，但可能需要很多步才能到达终点。

二、自定义训练循环与自动求导

在实际代码中，我们需要把梯度下降公式实现出来。传统做法是手动推导导数公式，然后代入更新。但在 TensorFlow 中，可以利用 自动微分（AutoDiff） 来自动计算梯度，避免繁琐的推导。

（1）损失函数

假设我们定义损失函数为：

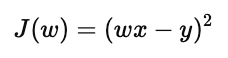
这里 w 是参数，x 是输入，y 是目标值。

（2）使用 tf.GradientTape

TensorFlow 提供 tf.GradientTape()，可以在其中记录运算过程，然后自动计算梯度：

w = tf.Variable(3.0)   # 初始化参数 w
x = 1.0                # 输入
y = 1.0                # 目标值
alpha = 0.01           # 学习率
iterations = 30

for iter in range(iterations):
    with tf.GradientTape() as tape:
        fwb = w * x
        costJ = (fwb - y) ** 2   # 定义损失函数
    dJdw = tape.gradient(costJ, w)  # 自动求导
    w.assign_sub(alpha * dJdw)      # 更新参数 w

（3）直观理解

• GradientTape 就像一个“录影机”，把前向传播的计算过程都记录下来；

• 当我们调用 tape.gradient() 时，它会自动“回放”这个过程，并计算导数；

• 最后使用 w.assign_sub() 来更新参数，完成一次梯度下降。

通俗理解：
你不需要自己算导数，TensorFlow 会帮你自动推出来。这就像有了一个随身的“梯度计算器”。

三、在 TensorFlow 中的完整实现

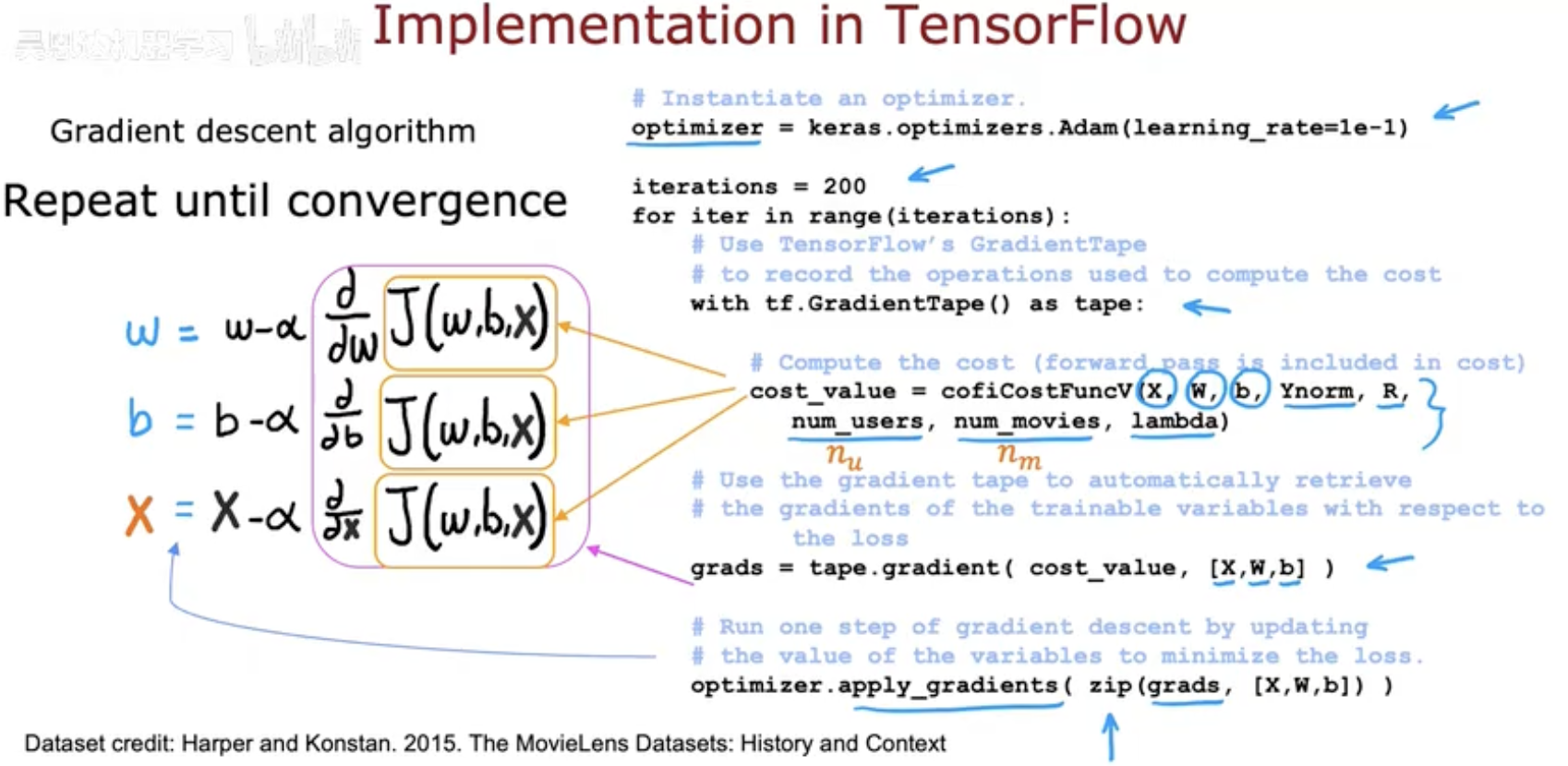
虽然可以通过 GradientTape 和手动更新参数来实现梯度下降，但在实际项目中，我们通常会用 TensorFlow 内置的优化器（Optimizer） 来简化流程。

（1）优化器的定义

TensorFlow 提供了多种优化器，比如 Adam、SGD、RMSprop 等。它们不仅能帮你更新参数，还能处理更复杂的场景（如自适应学习率）。

示例代码：

optimizer = tf.keras.optimizers.Adam(learning_rate=0.1)
iterations = 200

for iter in range(iterations):
    with tf.GradientTape() as tape:
        cost_value = cofiCostFuncV(X, W, b, Ynorm, R, num_users, num_movies, lambda_)
    grads = tape.gradient(cost_value, [X, W, b])   # 自动计算梯度
    optimizer.apply_gradients(zip(grads, [X, W, b]))  # 优化器更新参数

（2）核心思想

• tape.gradient：自动求导，得到梯度；

• optimizer.apply_gradients：用优化器来更新参数，而不需要手动写 assign_sub；

• 优势：代码更简洁，扩展性更强，可以方便地切换不同优化算法。

（3）直观理解

如果说 GradientTape 是一个“梯度计算器”，那么 优化器就是一个自动驾驶系统。你只需要告诉它损失函数和参数，它就会自动完成求导和更新，大大降低了手工计算的复杂性。

四、总结

在这篇文章里，我们从 梯度下降的公式 出发，逐步展示了它在 TensorFlow 中的实现方式：

1. 数学公式与直观理解

   • 梯度下降通过不断更新参数，沿着损失函数下降的方向前进，直到收敛。

   • 学习率 αα 决定了更新的速度和稳定性。

2. 自定义训练循环

   • 使用 tf.GradientTape() 记录运算，计算梯度，再手动更新参数。

   • 直观透明，适合学习和调试，能让人清楚看到梯度下降的每一步。

3. TensorFlow 的优化器实现

   • 借助内置优化器（如 Adam），我们不需要自己写更新公式，优化器会自动完成参数更新。

   • 代码更简洁、扩展性更强，更适合复杂模型和实际应用。