一、均值归一化简介
均值归一化(Mean Normalization) 是一种常见的数据预处理方法。它的核心思想是:将原始数据减去其均值,使得数据的中心值变为 0,从而消除不同数据之间的整体偏移。
在推荐系统中,用户的打分习惯差异很大:有些用户习惯给高分,有些用户则普遍打低分。如果不做处理,模型可能会把这种“用户个人偏好”当作电影本身的特征,导致推荐结果不准确。
通过均值归一化,我们能够 消除这种打分习惯的差异,让模型更关注用户和物品之间的相对关系,而不是绝对分数。
通俗理解:
就像有的人总是打高分(比如所有电影起步 4 星),有的人总是苛刻(很少打 5 星)。均值归一化就像给每个人“校正”了一下,让大家的打分基准都一致,这样推荐结果才更公平。
二、用户没有评分的情况

在实际的推荐系统中,经常会遇到一些用户完全没有打分的情况。例如图中的 Eve(用户5),她对任何电影都没有给过评分,导致她的整列数据都是空的(问号)。
这种情况会带来两个问题:
模型无法直接学习该用户的偏好
协同过滤需要根据已有评分来推断用户兴趣,但 Eve 没有任何历史数据,模型无法提取特征向量 w(j)w(j)。推荐结果偏差
如果简单把缺失值当作 0,会导致错误的结果,因为“没评分”并不等于“不喜欢”。
在数学建模中,这种情况被称为 稀疏性问题(Sparsity Problem)。当用户和电影数量庞大时,评分矩阵里大部分位置都是空的(未观测)。如何处理这些缺失值,是推荐系统的关键挑战之一。
这时,就需要 均值归一化 来帮忙:即使用户没有打过分,也可以利用电影的整体平均分来估计缺失值,作为一个合理的起点。
三、均值归一化的处理方法
为了解决用户打分习惯不同、甚至没有评分的情况,我们引入 均值归一化。核心做法是:
先计算每部电影的平均分 μi。
再把每个评分减去该电影的平均分,得到归一化后的评分。
(1)计算电影均值
例如,电影《Love at last》在不同用户中被打了分,平均值可能是 μ1=2.5。
(2)数据矩阵归一化
原始评分矩阵:
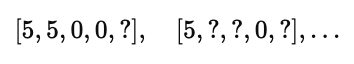
经过均值归一化后,每个数值都会减去该电影的均值 μi:
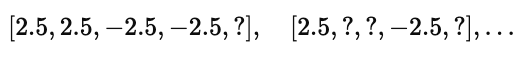
这样一来,不同用户的打分基准就被消除了,矩阵数据以 0 为中心,更利于模型训练。
(3)直观理解
如果某个用户的评分高于平均值,归一化结果为正数,表示“比大多数人更喜欢”。
如果评分低于平均值,结果为负数,表示“比大多数人更不喜欢”。
未评分的位置仍然保持为 “?”,等待模型预测。
通俗理解:就像班级里有些老师打分严格,有些宽松。如果直接比较分数,会产生偏差。但如果把每个人的分数减去该科目的平均分,再来比较,就更公平。
四、预测时如何恢复原始评分
在训练阶段,我们使用的是均值归一化后的评分矩阵。但在预测阶段,我们最终希望得到的仍然是用户的 实际评分(例如 1 到 5 星),而不是偏移后的值。
(1)预测公式
对于用户 j 在电影 i 上的预测分数,模型先得到归一化预测值:
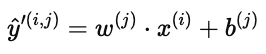
然后再加回电影的平均分 μi,得到最终预测结果:
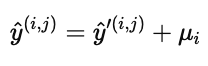
(2)为什么要加回均值?
因为训练时我们把每个评分减去了均值,预测值是相对于平均分的偏差。
如果不加回去,预测结果就会失去参考意义,无法映射回原始的评分区间。
(3)示例
假设某电影的平均分 μi=2.5,
模型预测 Alice 的归一化结果是 +1.0,则最终预测评分为 2.5+1.0=3.5。
如果预测结果是 −1.0,则最终评分为 1.5。
(4)直观理解
这就像考试时所有分数都按平均分做了平移(归一化),最后公布成绩时必须再加回平均值,才能得到真正的分数。
五、总结与应用
均值归一化(Mean Normalization) 的核心作用是:
通过减去均值,让数据分布以 0 为中心,减少不同用户打分习惯的差异;
即使遇到用户没有打分的情况,也可以利用物品的平均分作为基准,提升模型的稳定性;
在预测时,将归一化的预测结果加回均值,保证结果落在原始评分的合理区间。
优点:
提高推荐系统的公平性,让预测更贴近用户真实偏好;
缓解评分矩阵的稀疏性问题,改善模型训练效果;
保证不同用户的结果在同一尺度上可比较。
典型应用场景:
推荐系统:电影推荐、音乐推荐、电商商品推荐;
机器学习数据预处理:对数值型特征做均值归一化,加速模型收敛;
图像处理:对像素值减去均值,让图像输入更稳定。
简而言之,均值归一化是推荐系统和机器学习中的一个 小技巧、大作用,它帮助模型消除人为打分习惯带来的偏差,使得预测更精准、更公平。
