一、K-means 初始化的定义

K-means 的初始化是指在算法开始时，随机选择 KK 个数据点作为初始聚类中心。之后，算法会不断迭代，逐步调整这些中心的位置。

通俗理解：

先随便挑几个点当“代表”，再通过不断“重新选代表”，让每个小组里的成员和代表越来越接近。

二、K-means 初始化过程

• 左侧文字部分

  1. 选择聚类数 K<m，其中 m 是样本数量。

  2. 随机挑选 K 个训练样本。

  3. 将这 K 个样本作为初始聚类中心 μ₁,μ₂,…,μ_k。

• 右侧图示部分

  • 上图：黑点表示训练样本，红圈和蓝圈中各随机选出一个样本作为初始中心（红叉、蓝叉）。

  • 下图：红叉和蓝叉标记了两个被随机选出的初始聚类中心，其余黑点是待聚类的样本。

三、不同初始化的 K-means 聚类结果

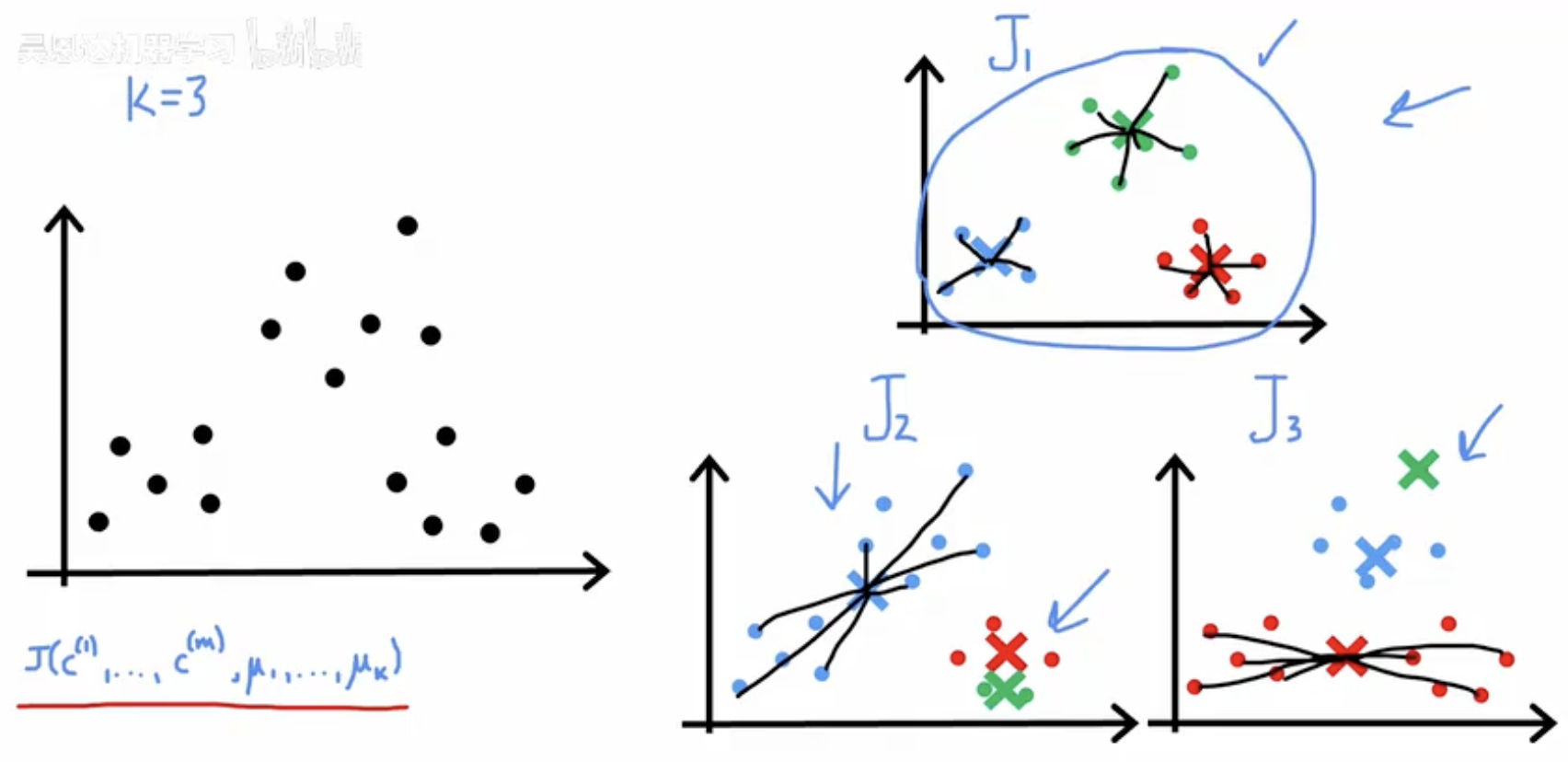
• 左侧：黑点为数据；标注 K=3。底部的 J(c⁽¹⁾,…,c^(m),μ₁,…,μ_K) 表示 K-means 的目标函数（由分配 c⁽ⁱ⁾ 和中心 μ_k 决定）。

• 右上（J₁）：出现三个紧凑的小簇（蓝/绿/红），每簇中心用“×”标出，辐射线连接到各自中心，蓝色大圈强调这一聚类结果对应的目标值为 J₁。

• 右下左（J₂）：多数样本被分到蓝簇，连线较长、形状拉伸，表示另一种初始化得到的聚类与其目标值 J₂。

• 右下右（J₃）：红簇沿水平方向分布较散，中心在中间（红“×”），蓝/绿簇在远处，表示第三种结果与其目标值 J₃。

要点：同一数据、同一 K，不同初始化产生不同的簇划分与不同的目标值 J₁,J₂,J₃；图中用蓝圈标出的结果表示被选中的那个。

四、K-means 的多次随机初始化与最小代价选择

• 顶部：For i = 1 to 100（图中注记：可做 50–1000 次）——表示进行多次随机尝试。

• 步骤1：Randomly initialize K-means. 用 k 个随机样本作为初始中心。

• 步骤2：Run K-means. 运行到收敛，得到分配 c⁽¹⁾,…,c^(m) 与中心 μ₁,…,μ_K。

• 步骤3：Compute cost function (distortion) 计算代价 J(c⁽¹⁾,…,c^(m),μ₁,…,μ_K)。

• 大括号外：Pick set of clusters that gave lowest cost J ——从所有尝试中选取代价 J最小的聚类结果作为最终结果。