一、K-means 优化目标与代价函数

• 符号说明（图左）

  • c⁽ⁱ⁾：样本 x⁽ⁱ⁾ 当前被分配到的簇索引，取值为 1,2,…,K。

  • μ_k：第 k 个簇的中心（centroid）。

  • μ_c⁽ⁱ⁾：样本 x⁽ⁱ⁾ 所在簇的中心，即由 c⁽ⁱ⁾ 指定的那个 μ_k。

• 代价函数（图中 “Cost function”）

  

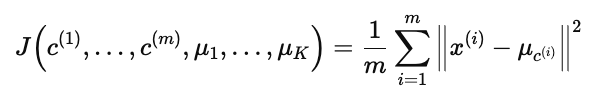
  • 式中 m 为样本总数；∥x⁽ⁱ⁾−μ_c⁽ⁱ⁾∥² 是第 i 个样本到其簇中心的距离平方。

  • 红色箭头在式子里标出的是 x⁽ⁱ⁾ 与 μ_c⁽ⁱ⁾；蓝色箭头与红字 Distortion 标明整项为“失真/畸变”。

  • 前面的 1/m 表示取平均。

• 优化目标（图下 “min …”）

  

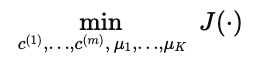
  含义：同时选择所有样本的簇分配 c⁽ⁱ⁾ 和各簇中心 μ_k，使上面的平均距离平方（失真）最小。

二、样本分配与簇中心的代价函数示意图

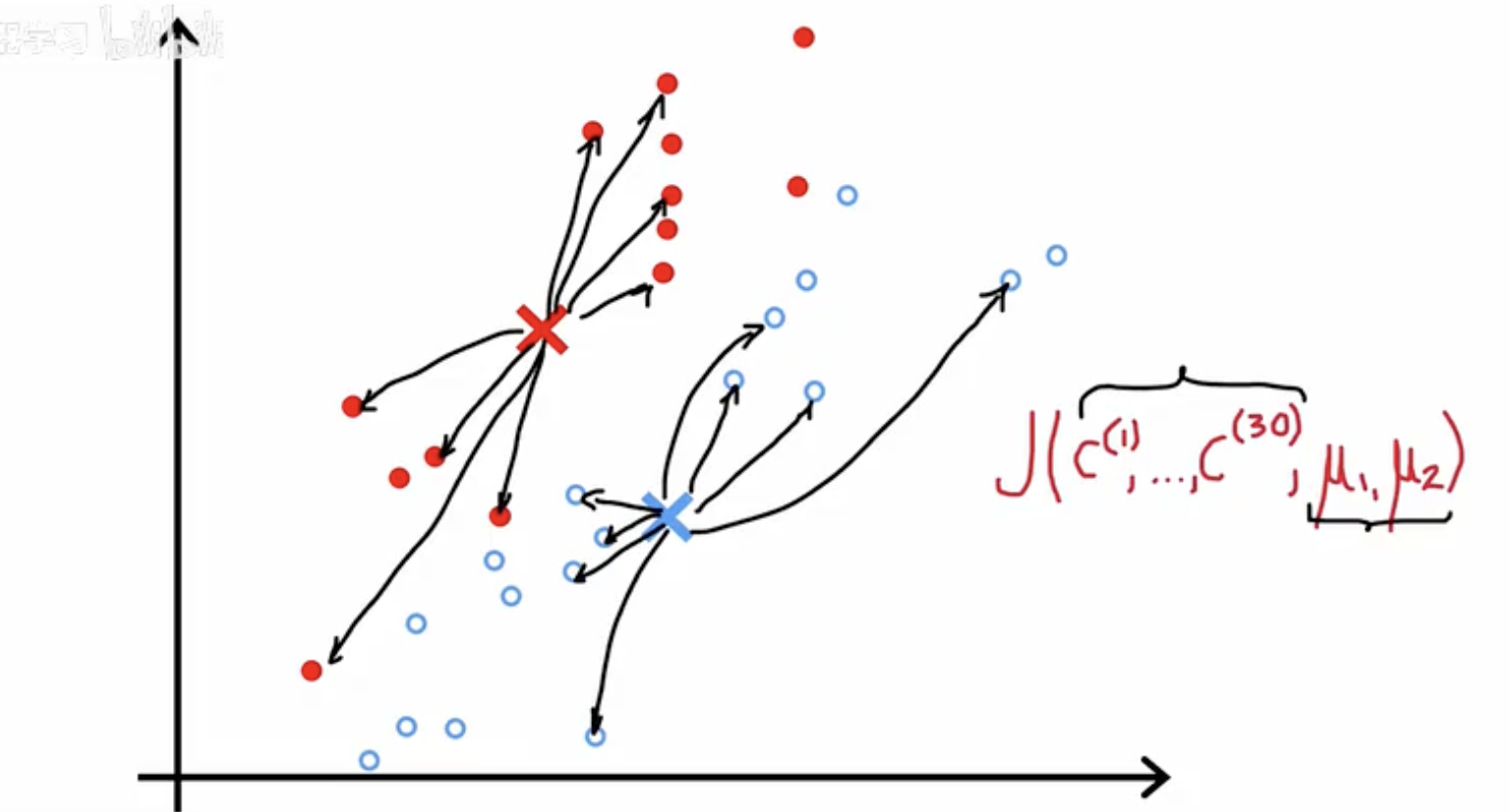
• 图中有两类点：红色实心点和蓝色空心点，分别属于两个不同簇。

• 红色叉号和蓝色叉号表示两个簇的中心（μ₁,μ₂）。

• 每个点通过一条箭头连接到对应的簇中心，表示样本 x⁽ⁱ⁾ 被分配到该簇，计算的是它与簇中心的距离。

• 图右边的公式 J(c⁽¹⁾,…,c⁽³⁰⁾,μ₁,μ₂) 表示总代价函数：这里共有 30 个样本（从 c⁽¹⁾ 到 c⁽³⁰⁾），并且有两个簇中心。

• 整幅图展示了 样本与簇中心的对应关系，以及如何用这些关系计算代价函数 J。

三、K-means 中簇中心更新与代价降低示意

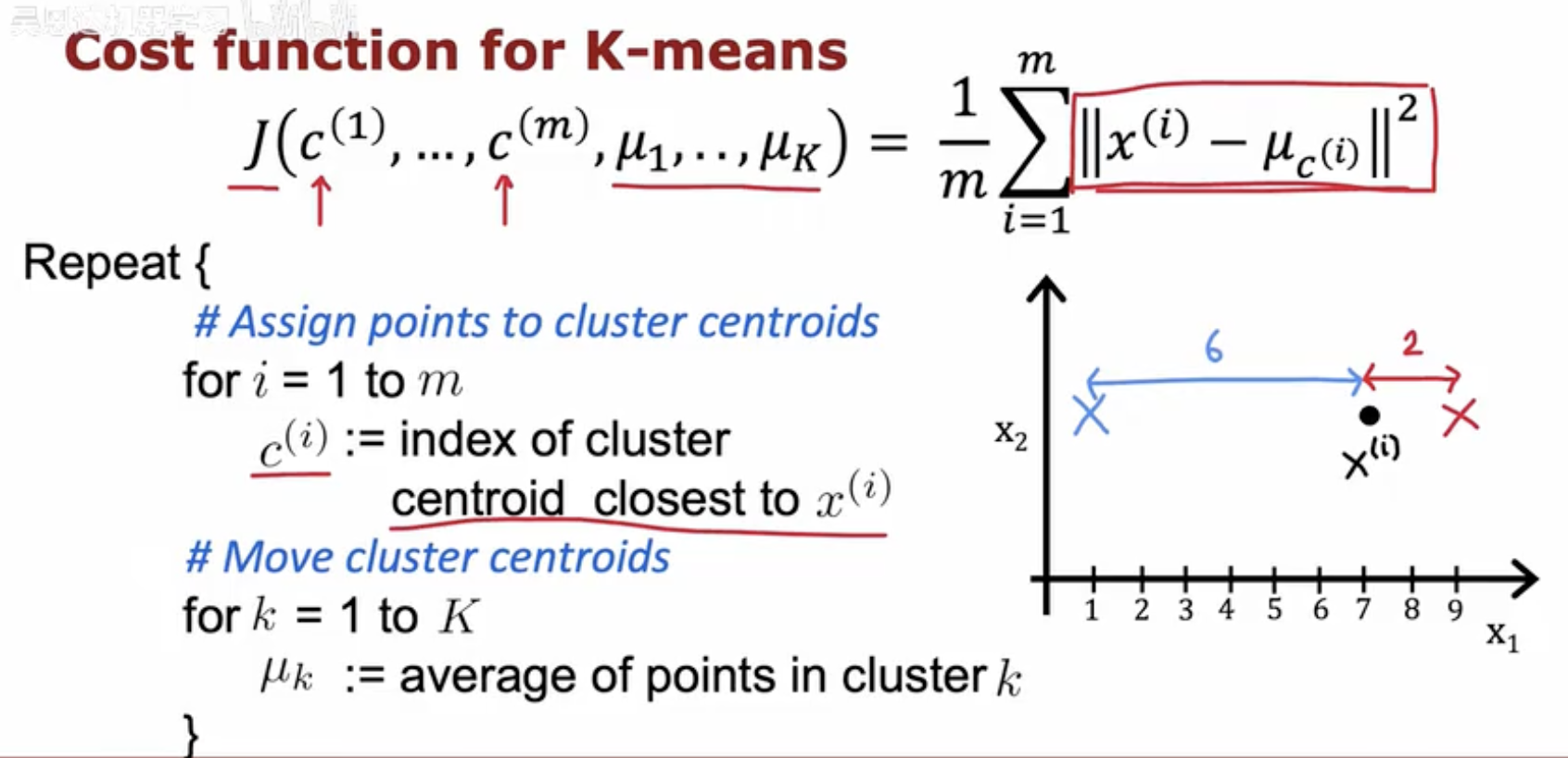
• 上方公式：展示了 K-means 的代价函数

  

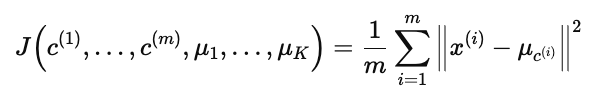
  其中每个样本与其所属簇中心的距离平方会被计算并取平均。

• 左下伪代码：说明算法的两个重复步骤

  1. Assign points：对于每个样本 x⁽ⁱ⁾，找到离它最近的簇中心，并将它分配给该簇，即更新 c⁽ⁱ⁾。

  2. Move centroids：对于每个簇 k，将中心 μ_k​ 更新为该簇中所有样本的平均值。

• 右侧示意图：

  • 黑点是样本 x⁽ⁱ⁾。

  • 蓝色和红色叉号分别代表两个簇的中心。

  • 图中显示了样本与两个中心的距离：到蓝色中心的距离为 6，到红色中心的距离为 2。

  • 因为红色中心更近，样本会被分配给红色簇。

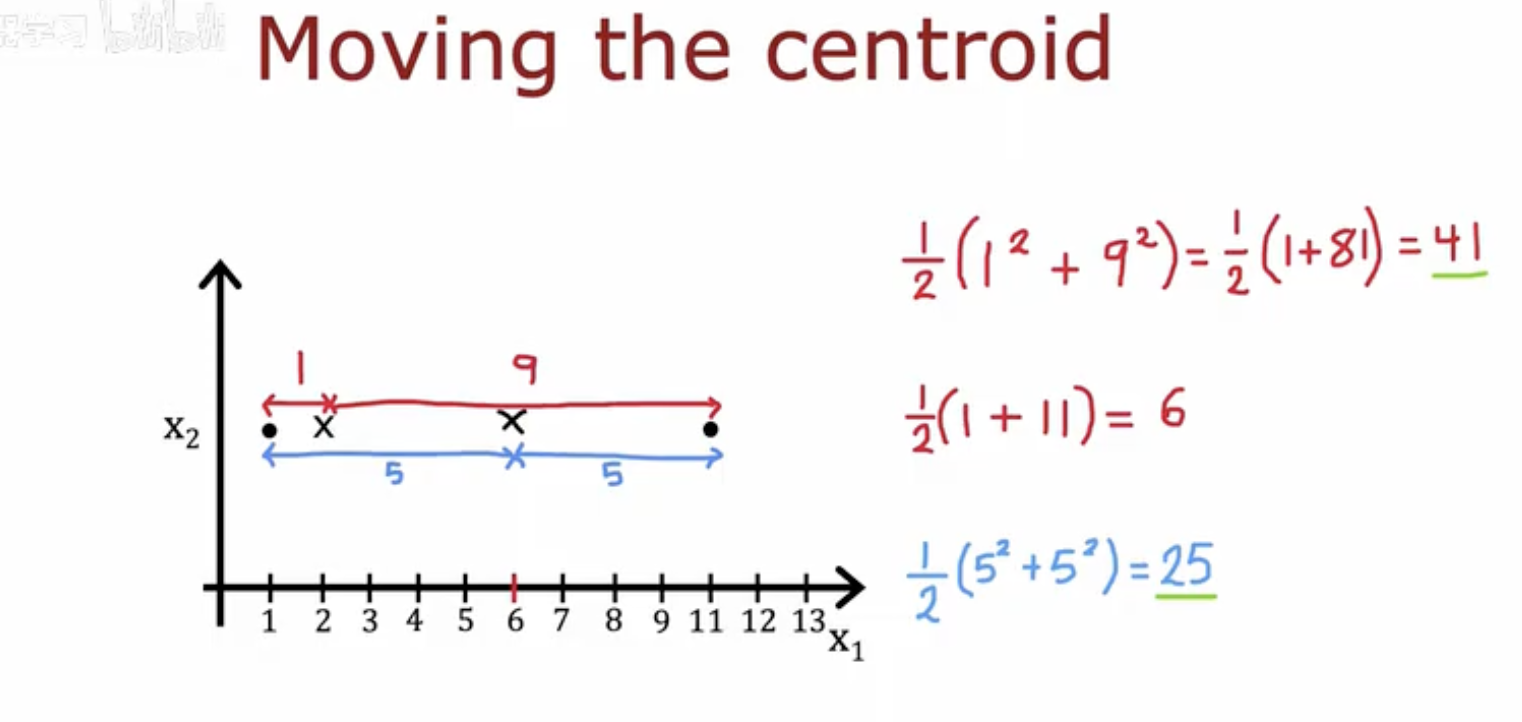
• 图中元素：

  • 两个黑点代表两个样本。

  • 中间的叉号是簇中心的位置。

  • 红色情况下，簇中心偏向左边，两个点到中心的距离分别是 1 和 9，对应代价为
    (1/2)(12+92)=41。

  • 蓝色情况下，簇中心在中间，两个点到中心的距离均为 5，对应代价为
    (1/2)(52+52)=25。

• 右侧公式：展示了不同中心位置时的代价计算。比较结果可以看到，把簇中心移到两个样本的中间，代价更小。