一、学习曲线的定义
学习曲线(Learning Curve)是一种用来衡量随着学习或练习的增加,完成某项任务所需时间和精力的变化趋势的图形。它通常呈现为随着学习时间的增加,效率逐渐提高,错误率逐渐降低的曲线形态。
通俗理解:
学习曲线就像我们学习新技能的过程,一开始可能会觉得很难,但随着时间的推移和不断的练习,我们会越来越熟练。
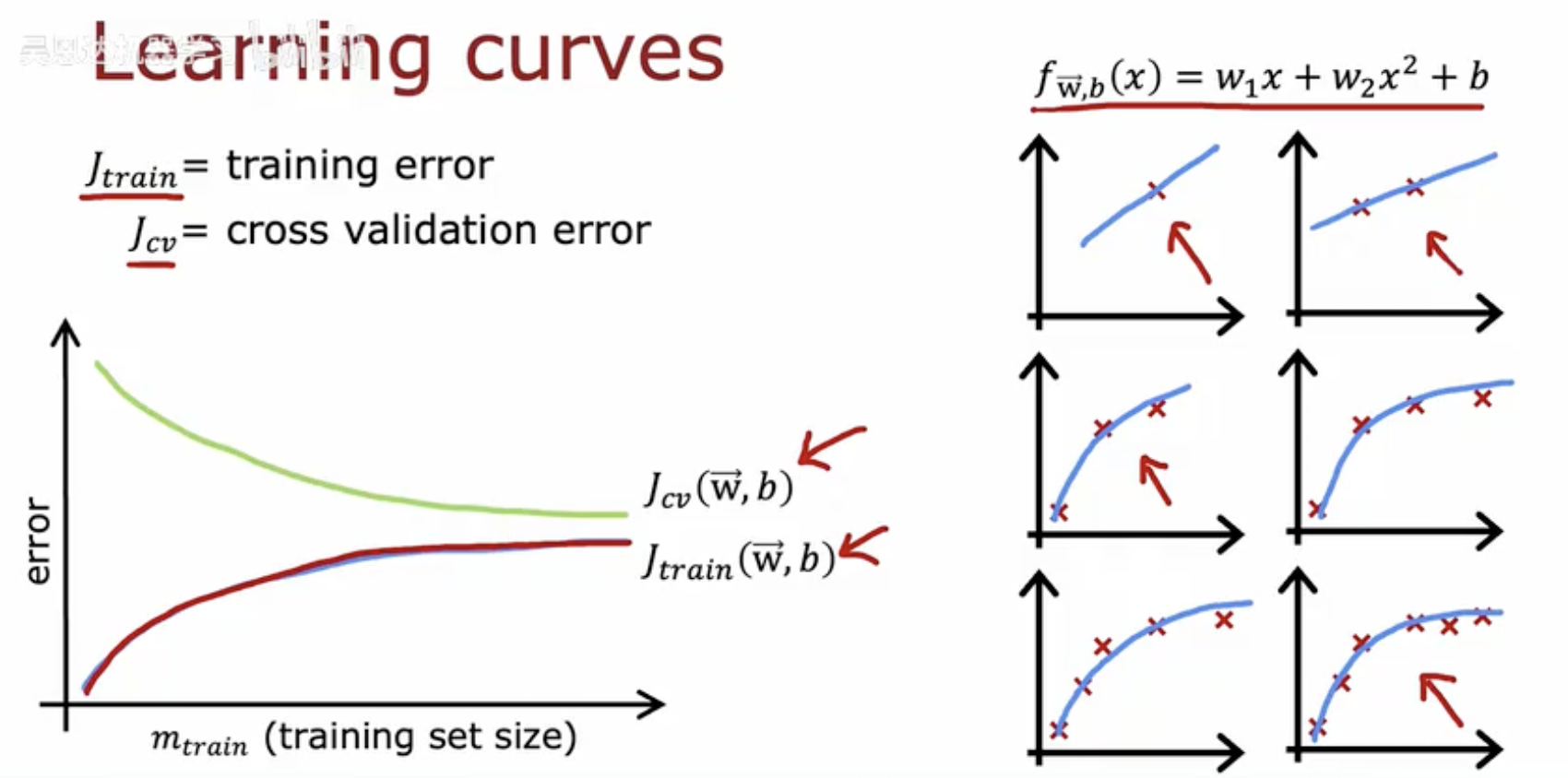
这张图片主要展示了学习曲线以及模型复杂度对训练误差和交叉验证误差的影响。
左侧图表(学习曲线):
横轴(mtrain):表示训练集的大小。
纵轴(error):表示误差。
Jtrain(训练误差):用红色线表示,随着训练集大小的增加,训练误差通常会逐渐增大,但最终会趋于一个稳定值。
Jcv(交叉验证误差):用绿色线表示,随着训练集大小的增加,交叉验证误差先减小后趋于稳定,最终达到一个较低的稳定值。
右侧图表(模型复杂度):
函数形式:fw,b(x)=w1x+w2x2+b,表示一个二次多项式函数。
上图:模型过于简单(欠拟合),无法很好地拟合数据,导致训练误差和交叉验证误差都较高。
中图:模型复杂度适中,能够较好地拟合数据,训练误差和交叉验证误差都较低。
下图:模型过于复杂(过拟合),虽然训练误差很低,但交叉验证误差较高,说明模型在训练集上表现很好,但在未见过的数据上表现较差。
二、高偏差的学习曲线
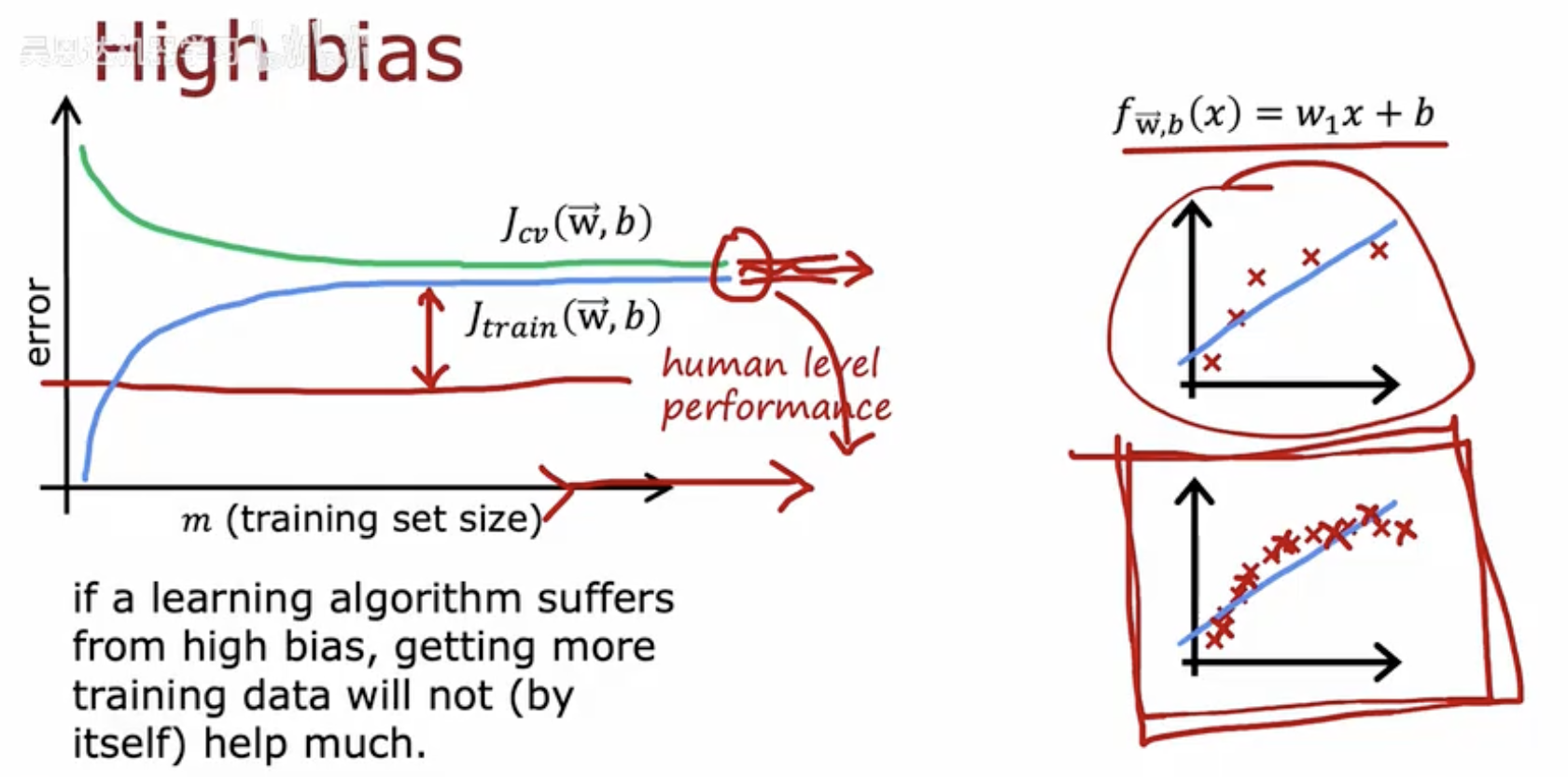
这张图片讨论了高偏差(High Bias)的情况。
左侧图表:
横轴(m):表示训练集的大小。
纵轴(error):表示误差。
Jtrain(w,b):训练误差,用红色线表示。
Jcv(w,b):交叉验证误差,用绿色线表示。
human level performance:表示人类水平的性能,是模型性能的理论上限。(基线)
图中显示,如果一个学习算法存在高偏差,增加更多的训练数据本身不会显著提高模型性能,因为模型过于简单,无法捕捉数据的复杂性。
右侧图表:
函数形式:fw,b(x)=w1x+b,表示一个线性函数。
图中展示了一个简单的线性模型试图拟合非线性数据的情况,导致高偏差。即使增加更多的数据,模型也无法有效降低误差,因为它无法捕捉数据的真实模式。
三、高方差的学习曲线

这张图片解释了高方差(High Variance)的情况。
左侧图表:
横轴(m):训练集的大小。
纵轴(error):误差。
Jtrain(w,b):训练误差,用蓝色线表示。
Jcv(w,b):交叉验证误差,用绿色线表示。
human level performance:人类水平的性能,表示模型性能的理论上限。(基线)
图中显示,如果一个学习算法存在高方差,增加更多的训练数据可能会有所帮助,因为模型过于复杂,容易过拟合。
右侧图表:
函数形式:fw,b(x)=w1x+w2x2+w3x3+w4x4+b,表示一个高阶多项式函数。
图中展示了一个复杂的模型试图拟合数据的情况,导致高方差。增加更多的数据可以帮助模型更好地泛化,减少过拟合。
四、调试学习方法,减少误差

这张图片讨论了如何调试一个学习算法,特别是当它在预测中产生不可接受的大误差时。
公式部分:
J(w,b):表示正则化的线性回归成本函数。
第一项:是平方误差损失,衡量模型预测与实际值之间的差异。
第二项:是正则化项,包含正则化参数 λ,用于控制模型复杂度。
调试建议:
获取更多训练样本:可以解决高方差问题。
尝试更小的特征集:可以解决高方差问题。
尝试获取更多特征:可以解决高偏差问题。
尝试添加多项式特征:可以解决高偏差问题。
尝试减小 λ:可以解决高偏差问题。
尝试增加 λ:可以解决高方差问题。
