一、引言
在数据分析与机器学习中,“距离”是衡量样本之间相似度的核心概念。我们常见的欧氏距离(Euclidean Distance)与曼哈顿距离(Manhattan Distance),都基于坐标差值来计算样本间的空间距离。然而,它们都隐含着一个强假设——各个特征之间是相互独立的,并且在相同的度量尺度下。
但在现实世界中,这个假设往往并不成立。
在一个包含多个变量的数据集中,不同特征之间往往存在一定的相关性(correlation)。例如,在人体测量数据中,人的身高与体重、胸围与腰围都存在明显相关关系。如果我们忽略这些相关性,仅用欧氏距离去度量样本间的差异,就可能产生错误的判断。
为了克服这一局限,印度统计学家 P.C. Mahalanobis 于 1936 年提出了 马氏距离(Mahalanobis Distance)。
这种距离度量方法通过引入协方差矩阵(Covariance Matrix),对不同特征的方差与相关性进行校正,从而能够在一个更合理的统计空间中衡量样本间的真实差异。
换句话说,马氏距离不仅考虑了两个样本之间的“数值差”,更考虑了这种差异在整体数据结构中的“合理性”。
因此,它在多变量统计分析、异常检测(Outlier Detection)、模式识别(Pattern Recognition)等领域具有极高的实用价值。
二、马氏距离的数学定义
马氏距离(Mahalanobis Distance)是一种考虑变量间相关性(correlation)的距离度量方法。它通过协方差矩阵对数据进行标准化,使得每个维度的方差相同,并消除了变量间的线性相关影响。其数学定义如下:

其中:
x,y 为两个样本向量(维度为 n)。
Σ 是样本总体的协方差矩阵(Covariance Matrix)。
Σ−1 表示其逆矩阵。
上标 T 表示转置。
从定义可以看出,马氏距离在形式上与欧氏距离类似,但多了一个关键的权重项——Σ−1。这意味着在计算样本间距离时,马氏距离会根据特征之间的方差与相关性重新调整各维度的权重。
1. 与欧氏距离的比较
如果协方差矩阵为单位阵 I,即所有特征之间完全独立且方差为 1,那么:

此时,马氏距离就退化为欧氏距离。
这表明欧氏距离其实是马氏距离的一种特殊情况。
2. 协方差矩阵的作用
协方差矩阵用于描述变量之间的线性关系。当某些维度之间存在强相关时,马氏距离会“惩罚”这种重复信息,从而在距离计算中减少冗余。例如:
若两个特征几乎完全线性相关,它们提供的信息实际上相同,马氏距离会自动降低它们的综合影响;
若某个特征的方差过大(数据分布范围广),它在距离计算中不会被过度放大,因为协方差矩阵的标准化会自动调整其尺度。
通过这种方式,马氏距离提供了一种统计意义上的公平度量方法,能够更准确地反映样本间的真实差异。
三、马氏距离的几何意义
欧氏距离衡量的是两个点在笛卡尔坐标系中的直线距离,假设所有维度的方差相同且互不相关,因此在几何上对应的是一个圆形等距线(circle)。
而马氏距离则不同,它考虑了不同维度之间的方差与协方差。
这意味着在高维空间中,距离的“等距线”不再是圆形,而是一个根据数据分布拉伸或旋转后的椭圆(ellipse)。
1. 变量间相关性的影响
当两个变量高度相关时,它们在数据空间中的分布会形成一条倾斜的“数据带”。此时,欧氏距离计算出的结果会夸大样本间的差异,因为它没有考虑到变量之间的重叠信息。
马氏距离通过协方差矩阵对这种相关性进行校正,使得距离的计算方向更符合数据分布的主轴。
因此,它能在去除变量间冗余的同时,保持整体结构的真实差异。
2. 等距线的形状
在二维空间中:
欧氏距离的等距线是一个圆形,意味着所有方向上的尺度相同;
马氏距离的等距线是一个椭圆形,其长轴和短轴方向由协方差矩阵的特征向量决定,长度由特征值大小控制。
这说明马氏距离能够根据数据的实际分布方向,动态调整“距离度量”的方向与尺度。换句话说,它不是盲目地在原坐标系下测量,而是根据数据的结构重新定义了空间的几何形态。
3. 几何意义总结
马氏距离提供了一种自适应的几何度量方式:
当数据各维度独立且方差相同,它退化为欧氏距离;
当数据存在相关性或不同尺度时,它会调整测量空间,使距离更能反映样本在统计意义上的真实差异。
因此,从几何角度看,马氏距离就是在“拉伸”与“旋转”坐标系后再测量的欧氏距离。它不仅计算“距离”,更反映了样本间在数据分布结构中的相似程度。
四、示例与计算步骤
为了更直观地理解马氏距离的计算过程,我们通过一个具体的数值例子来演示。假设我们有一个二维数据集,包含以下两个样本点:

并且我们知道整个数据集的协方差矩阵为:
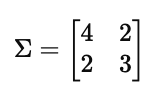
计算步骤如下:
1. 计算样本差向量

2. 计算协方差矩阵的逆矩阵

3. 代入马氏距离公式

将上式展开:
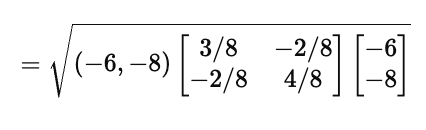
计算结果:

4. 结果解释
马氏距离 D(x,y)=4.69 表明,在考虑数据分布和变量相关性后,点 x 与 y 的统计距离为 4.69。
若直接用欧氏距离计算:

可以看出,欧氏距离明显更大,因为它没有考虑特征间的相关性。
这也说明马氏距离对数据结构更加敏感,能在特征维度存在冗余或不同尺度时提供更合理的距离度量。
五、应用与实际意义
马氏距离在统计学、机器学习与数据挖掘中都有着非常广泛的应用,它的核心价值在于能够识别多变量空间中具有异常特征或不同结构的点。
由于它引入了协方差矩阵,因此特别适用于高维数据分析、异常检测与模式识别等场景。
1. 异常检测(Outlier Detection)
马氏距离的一个经典应用是多维异常值检测。
在一个多维数据集中,如果某个样本点距离数据分布中心的马氏距离过大(通常超过某一阈值,如 3 或 4),就可以被认为是异常点(Outlier)。
这在工业检测、金融欺诈识别和医学诊断中非常有用。
例如,在产品质量检测中,马氏距离可以用来判断一个产品的特征组合(如长度、重量、密度等)是否明显偏离了正常生产范围。
2. 模式识别与分类(Pattern Recognition and Classification)
在模式识别中,如人脸识别、语音识别等,马氏距离常被用作判别度量标准。
不同类别的数据往往具有不同的协方差结构,通过使用类别对应的协方差矩阵,可以判断新样本点属于哪个分布最为合理。
例如,假设我们有两个类别 C1 与 C2,各自具有均值向量 μ1,μ2μ1,μ2 和协方差矩阵 Σ1,Σ2。
对于一个未知样本 x,若其到 μ1 的马氏距离小于到 μ2 的距离,则可判定它属于 C1。
这种思想被广泛应用于高斯判别分析(GDA)与贝叶斯分类器(Bayesian Classifier)中。
3. 降维与聚类分析(Dimensionality Reduction and Clustering)
在主成分分析(PCA)或聚类算法(如 K-Means)中,马氏距离也可以帮助我们更准确地度量样本间的相似度。
相比欧氏距离,它能减少由于特征方差不均或尺度不同带来的偏差。
例如,当样本分布呈现椭圆形时,欧氏距离可能错误地认为两个点相似,而马氏距离能够更准确地反映真实的“统计距离”。
4. 多维特征匹配(Feature Matching in Computer Vision)
在计算机视觉中,马氏距离常被用于特征匹配,如 SIFT、SURF 等特征描述符的比较。
它能够识别哪些特征点在高维特征空间中真正相似,而非仅在数值上接近,从而提升匹配的鲁棒性。
