一、引言

在数据科学与机器学习的世界中，“距离”是一个极为核心的概念。无论是在聚类算法、相似度计算，还是在分类任务中，衡量两个样本之间的差异都离不开距离度量。而“Manhattan Distance（曼哈顿距离）”，便是其中最直观、最经典的一种。

曼哈顿距离（Manhattan Distance）又被称为城市街区距离（City Block Distance）或L₁距离（L₁ Norm）。它的名称来源于美国纽约的曼哈顿区——那里的街道呈规则的网格状布局。假设你站在一个街角，要走到另一个街角，若只能沿着南北或东西方向前进（不能斜着穿越街区），那么你行走的总路程就是曼哈顿距离。这种“拐弯前进”的路线正是曼哈顿距离的几何意义。

与“Euclidean Distance（欧氏距离）”相比，欧氏距离是“直线距离”，而曼哈顿距离则更像是“实际行走的路径距离”。两者在不同任务中有各自的优势：前者强调精确的空间几何关系，而后者在高维空间和稀疏数据中往往表现更稳健。

在数据分析、推荐系统、文本挖掘、图像识别等领域，曼哈顿距离被广泛应用。它不仅计算简单、解释直观，还对异常值具有更强的鲁棒性（robustness）。因此，无论是在理论研究还是工程实践中，它都是理解“相似度与差异”的重要起点。

二、曼哈顿距离的数学定义

在数学上，曼哈顿距离定义为两个点在各个坐标轴上的绝对差值之和。
如果我们有两个 n 维空间中的点 i=(x_i1,x_i2,...,x_in) 和 j=(x_j1,x_j2,...,x_jn)，
那么它们之间的曼哈顿距离定义如下：

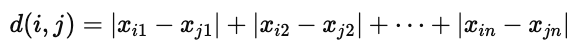
这意味着，曼哈顿距离并不计算“直线距离”，而是逐维度地对比两个点在各个坐标上的差异，然后将这些差值的绝对值相加。换句话说，它衡量的是两点之间沿着坐标轴方向“走多少步”才能相互到达。

图示示例：

在下面这张图片中，展示了两个四维点 (22,1,42,10) 与 (20,0,36,8) 的曼哈顿距离计算过程：

通过逐维计算：

因此，这两个点之间的曼哈顿距离为 11。

从直观角度来看，这个结果代表：若我们必须沿着坐标轴方向（而不是对角线）从第一个点走到第二个点，所需要走的“步数”总和就是 11。

这种逐维度的计算方式使曼哈顿距离在处理高维数据时尤其有意义，因为它避免了平方项（不像欧氏距离那样平方求和），因此对极端值（outliers）不敏感，具有较好的稳定性。

三、计算示例与可视化说明

理解曼哈顿距离最直观的方式之一，就是通过实际计算。
我们可以把它想象成一种“沿坐标轴前进的路径长度”，每个维度的差异都会对最终距离产生线性影响。

示例表格分析

表格中展示了一个简单的二维样本集合，其中目标点为

x=(1.4,1.6)

并与五个样本点进行比较（分别记为 A₁,A₂）。
每一行都计算了该样本与目标点之间的曼哈顿距离。

结果解读

从结果可以看到，第 1 个样本点的曼哈顿距离最小（0.2），说明它与目标点 (1.4,1.6) 最相似。
相反，第 2 个样本点的距离最大（0.9），说明它与目标点差异较大。
这类距离计算在聚类或最近邻算法中非常常见，例如在 KNN（K-Nearest Neighbors） 算法中，模型会基于距离最小的样本来判断新样本的类别。

几何直觉

若将这些点绘制在二维平面上，会发现曼哈顿距离的路径并非“直线连线”，而是“由水平和垂直线段组成的折线路径”。
因此，在相同两点间，曼哈顿距离总是大于或等于欧氏距离。

这种特性使得它在模拟“城市道路网格”、“棋盘路径”或“离散栅格移动”等问题时非常实用。

四、与其他距离度量的比较

虽然曼哈顿距离的概念简单，但它与其他距离度量方法之间存在着深刻的数学联系。理解这些关系，有助于我们在实际问题中正确选择“距离函数”，以获得更合理的分析结果。

1. 与欧氏距离（Euclidean Distance）的比较

欧氏距离（L₂范数）是我们最熟悉的“直线距离”，其计算方式为：

两者的主要区别如下：

比较维度	曼哈顿距离 (L₁)	欧氏距离 (L₂)
路径	沿坐标轴的折线	直线连接两点
运算复杂度	简单（无平方和平方根）	稍复杂（需平方根）
对异常值敏感性	低（线性变化）	高（平方放大差距）
几何意义	菱形等距线	圆形等距线
适用场景	稀疏数据、高维特征	连续数值、物理空间

举例来说，在高维空间中，欧氏距离容易受到某个维度异常值的影响；而曼哈顿距离对每个维度的变化都“平等对待”，因此在数据噪声较多的情况下表现更稳健。

2. 与闵可夫斯基距离（Minkowski Distance）的关系

事实上，曼哈顿距离和欧氏距离都是“闵可夫斯基距离（Minkowski Distance）”的特例。

闵可夫斯基距离的一般形式为：

当 p=1 时，就是曼哈顿距离；
当 p=2 时，就是欧氏距离；
而当 p→∞ 时，就变成了切比雪夫距离（Chebyshev Distance）。

因此，曼哈顿距离可以看作是一种“线性度量方式”，它衡量的是所有维度差值的绝对总和。而欧氏距离通过平方和再开方，更强调维度之间差异的综合影响。

3. 总结：选择哪种距离？

不同的距离度量方法适用于不同的数据特征：

曼哈顿距离：适合高维稀疏数据，如文本向量、图像像素、推荐系统评分矩阵。
欧氏距离：适合低维连续空间，如几何距离、物理坐标。
切比雪夫距离：用于“最大维度差异”主导的情况，如棋盘距离。

换句话说，如果我们希望度量“整体差异”，选择曼哈顿距离更稳妥；
如果我们希望强调“直观几何距离”，欧氏距离会更合适。

五、应用场景与优势

曼哈顿距离不仅是一个数学定义，更是一种在实际问题中被广泛采用的数据相似性度量方法。
其计算简单、稳定性强的特性，使它成为各类算法中重要的“距离基石”。

1. 聚类分析（Clustering Analysis）

在聚类任务（如 K-Means 或 K-Medoids）中，样本之间的相似性决定了聚类结果的质量。
如果数据维度较多或存在异常点，使用欧氏距离往往会导致聚类中心偏移。
此时，曼哈顿距离能更准确地反映样本的平均差异，因为它对每个维度的变化都线性处理。

例如：

在客户消费数据聚类中，单个维度（如一次异常高消费）不会严重拉远距离；
在图像或语音特征聚类中，曼哈顿距离可保持特征的整体差异结构。

2. 推荐系统（Recommendation Systems）

在基于邻域的方法中（如 User-Based CF 或 Item-Based CF），
曼哈顿距离常用于度量用户之间或物品之间的“行为差异”。

例如：

两个用户的购买历史向量可以视为一组二元特征（买过/没买过）；
曼哈顿距离越小，说明用户在购买偏好上越接近。

这种方法对评分矩阵中稀疏和不均衡的情况尤为适用，
因为它不会过分放大某些维度上的差异。

3. 异常检测（Anomaly Detection）

在异常检测中，我们常需要找出“与多数样本距离较远”的点。
相比欧氏距离，曼哈顿距离对于异常值更鲁棒，因为它不会将单个特征的巨大偏差平方放大。

举例：

在网络流量监控中，某个时间段的请求数异常升高；
在传感器数据中，某个维度出现极端读数；
这时曼哈顿距离能稳定地衡量整体偏离程度，不易被极值扰动。

4. 文本与自然语言处理（Text & NLP）

在 NLP 中，单词、句子或文档常被表示为高维稀疏向量（如词袋模型、TF-IDF 向量）。
曼哈顿距离能有效衡量这些向量的差异程度，而不会因高维稀疏性导致过度放大。

例如：

比较两个新闻标题的词频差异；
测量两位用户在话题词汇上的距离；
用于短文本分类和相似问题检测。

5. 优势总结

特性	曼哈顿距离优势
计算复杂度	无平方与平方根，速度快
稳定性	对异常值不敏感
可解释性	各维度差异直接累加，意义直观
稀疏适应性	高维稀疏空间表现优良
几何意义	体现“路径长度”而非“直线距离”

简而言之，曼哈顿距离提供了一种线性、可解释、鲁棒的相似性度量方式，
它在高维、噪声或离散型特征中往往比欧氏距离表现更稳定。

六、总结

曼哈顿距离（Manhattan Distance）是一种基础却极具代表性的距离度量方法。
它通过计算各维度之间的绝对差值之和，衡量样本间的整体差异。
与欧氏距离相比，它放弃了平方与开方运算，更关注“沿坐标轴前进的路径长度”，因此在高维稀疏数据、存在噪声或异常值的场景中表现更加稳定。

从城市街区的几何启发，到机器学习算法的核心组件，曼哈顿距离的思想在多个领域中得到了广泛应用。
无论是聚类分析、推荐系统、文本相似度计算，还是异常检测与数据压缩，它都能提供一种简单、直观、鲁棒的相似性度量方式。

更重要的是，曼哈顿距离不仅是一个孤立的公式，它还与其他度量方法紧密相关：

当 p=1 时，它是闵可夫斯基距离的特殊形式；
当 p=2 时，公式转化为欧氏距离；
当 p→∞ 时，又得到切比雪夫距离。

因此，曼哈顿距离在整个“距离度量体系”中占据了重要位置。它为理解更复杂的距离函数打下了直观基础，也为我们提供了一种在不完美世界中衡量差异的简洁方式。

菜单

Manhattan Distance｜曼哈顿距离

分享