一、基尼指数(Gini Index)
1.1 基尼指数的基本定义(Definition of Gini Index)
在分类问题中,一个节点内部样本越“混乱”,该节点就越不纯;反之,如果节点中的样本几乎都属于同一类,则说明该节点分类效果较好。
基尼指数正是用来度量这种“混乱程度”的指标之一,其定义如下:
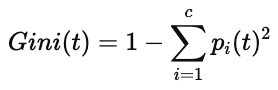
其中:
pi(t) 表示节点 tt 中属于第 i 类别的样本比例
c 表示类别总数
基尼指数的取值范围为:
最小值为 0:当节点中的样本全部属于同一类别时,比如全是正类或全是负类,此时节点是完全纯净的。
最大值为 1−1/c:当样本在所有类别中均匀分布时,此时节点最混乱,对分类最不利。
在实际中,CART、SLIQ、SPRINT 等决策树算法都会使用基尼指数作为划分标准之一。

1.2 二分类问题下的 GINI 特性(Gini for Binary Classification)
对于二分类问题,若设其中一类的比例为 p,另一类为 1−p,则基尼指数可进一步简化为:
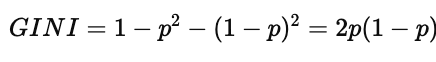
这个式子有一个非常直观的重要特性:
当 p=0 或 p=1 时,GINI = 0,说明节点完全纯;
当 p=0.5 时,GINI 达到最大值 0.5,说明两类样本完全混合。
图中还用不同的样本分布展示了这一变化规律,例如:
C1:0, C2:6 → Gini = 0
C1:1, C2:5 → Gini ≈ 0.278
C1:2, C2:4 → Gini ≈ 0.444
这些例子非常直观地说明:
样本越接近平分,GINI 越大;越偏向某一类,则 GINI 越小。

1.3 单个节点的 Gini 计算(Computing Gini Index of a Single Node)
在实际的决策树构建中,我们经常需要计算某一个节点的基尼指数,比如判断是否继续分裂。
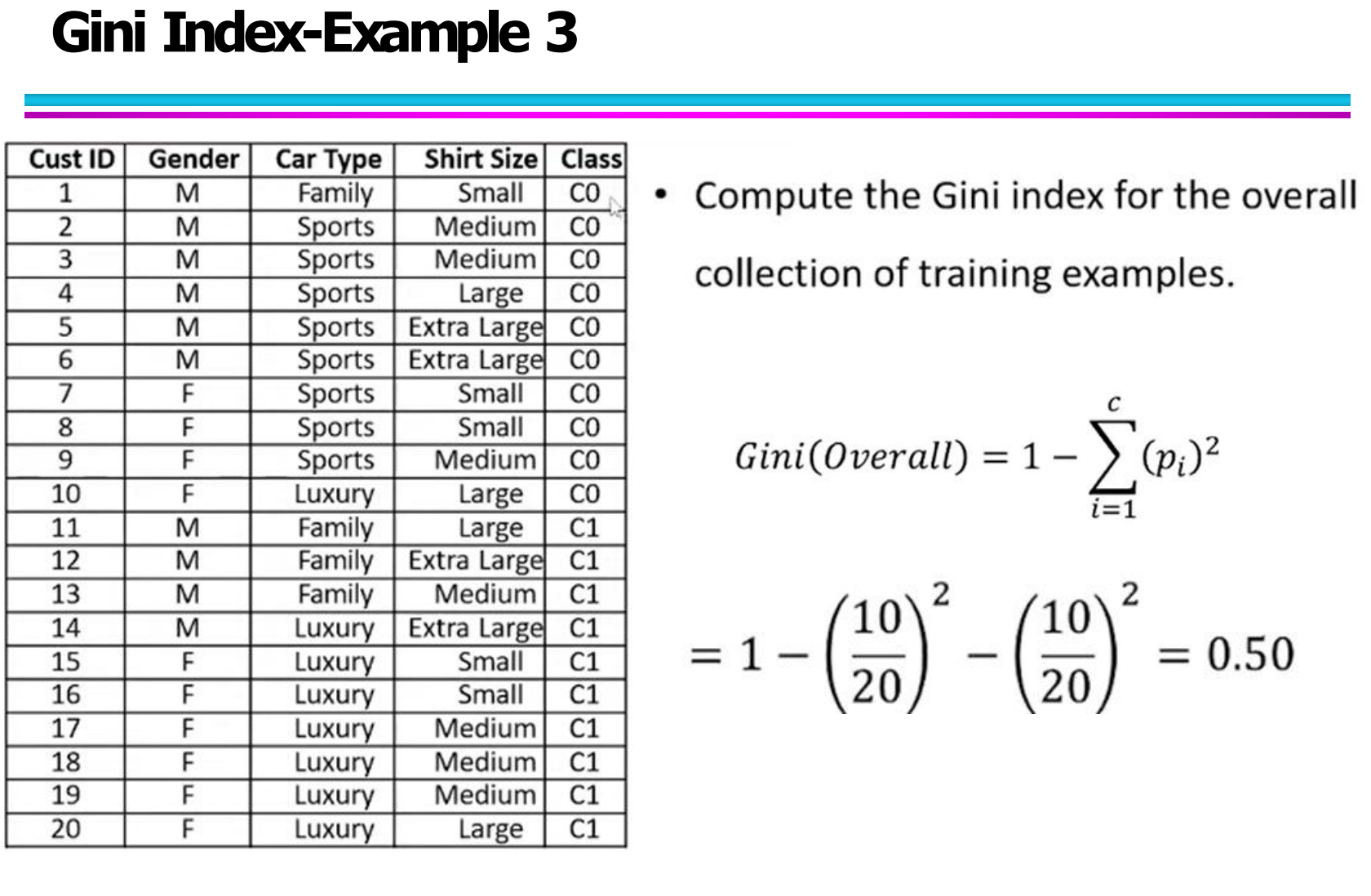
以你给出的示例为例:
情况 1:
此时:
P(C1) = 0 / 6 = 0
P(C2) = 6 / 6 = 1
代入公式:
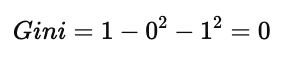
说明该节点是完全纯节点,无需继续分裂。
情况 2:
则:
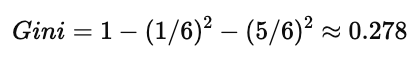
说明该节点已经出现类别混杂,可以继续考虑分裂。

1.4 多子节点划分的 Gini 计算(Gini Index for Node Splits)
在决策树的节点划分过程中,核心问题并不是单个节点的 GINI,而是:
划分后整体是否更“纯”?
当一个父节点被分成 k 个子节点时,整体的 Gini 值计算公式为:
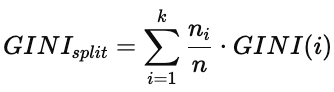
其中:
ni:第 i 个子节点的样本数
n:父节点总样本数
GINI(i):第 i 个子节点的基尼指数
这说明:
每个子节点的 GINI 不是简单平均,而是按照其样本数量进行加权求和。
决策树在实际选择划分属性时,通常遵循:
选择使 GINI_split 最小 的那个划分方式。
因为 GINI_split 越小,表示子节点整体越纯,分类效果越好。

二、不同属性下的 Gini 计算与分裂策略
2.1 二元属性:Binary Attribute 的 Gini 分裂
当属性是二元属性(如:Yes / No,True / False),其分裂方式非常直接,只会产生两个子节点。
在图片中,属性 B? 被用作测试条件,将父节点分裂成两个节点 N1(Yes)和 N2(No)。每个子节点上都有不同类别(C1 和 C2)的分布。
核心计算逻辑如下:
先计算每个子节点的 Gini 值:
对 N1 和 N2 分别根据类别比例代入 Gini 公式:
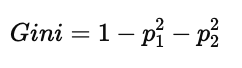
然后对两个子节点进行加权:
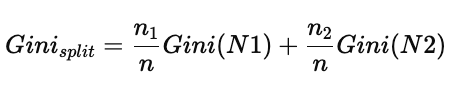
最后用 父节点 Gini - 分裂后的 Gini 得到 Gini 增益(类似信息增益的概念)。
在给出的示例中:
父节点 Gini = 0.486
分裂后加权 Gini = 0.361
所以 Gain = 0.486 − 0.361 = 0.125
说明这个分裂是有效降低不纯度的,是一个“好”的划分。

2.2 离散类别属性:Categorical Attribute 的 Gini 分裂
当属性是离散类别属性(如:CarType = Family / Sports / Luxury),常见有两种分裂策略:
① 多路分裂(Multi-way split)
即每个属性值对应一个子节点,例如:
Family
Sports
Luxury
系统先统计每个类别下,各个类标签(C1、C2)的样本数量,然后计算整体的加权 Gini。
这种方式的优点是:
信息更细致,保留更多原始结构。
但缺点是:
容易造成树过于复杂,甚至过拟合。
② 二路分裂(Two-way split)
将多个类别合并成两组,例如:
{Sports} 与 {Family, Luxury}
或 {Sports, Luxury} 与 {Family}
通过不同组合尝试,计算每种二分方式的 Gini,选出那个使 Gini 最小的组合。
图中可以看到:
不同的分裂组合,最终 Gini 不同,哪个 Gini 最小,哪个就是当前属性的最优划分方式。

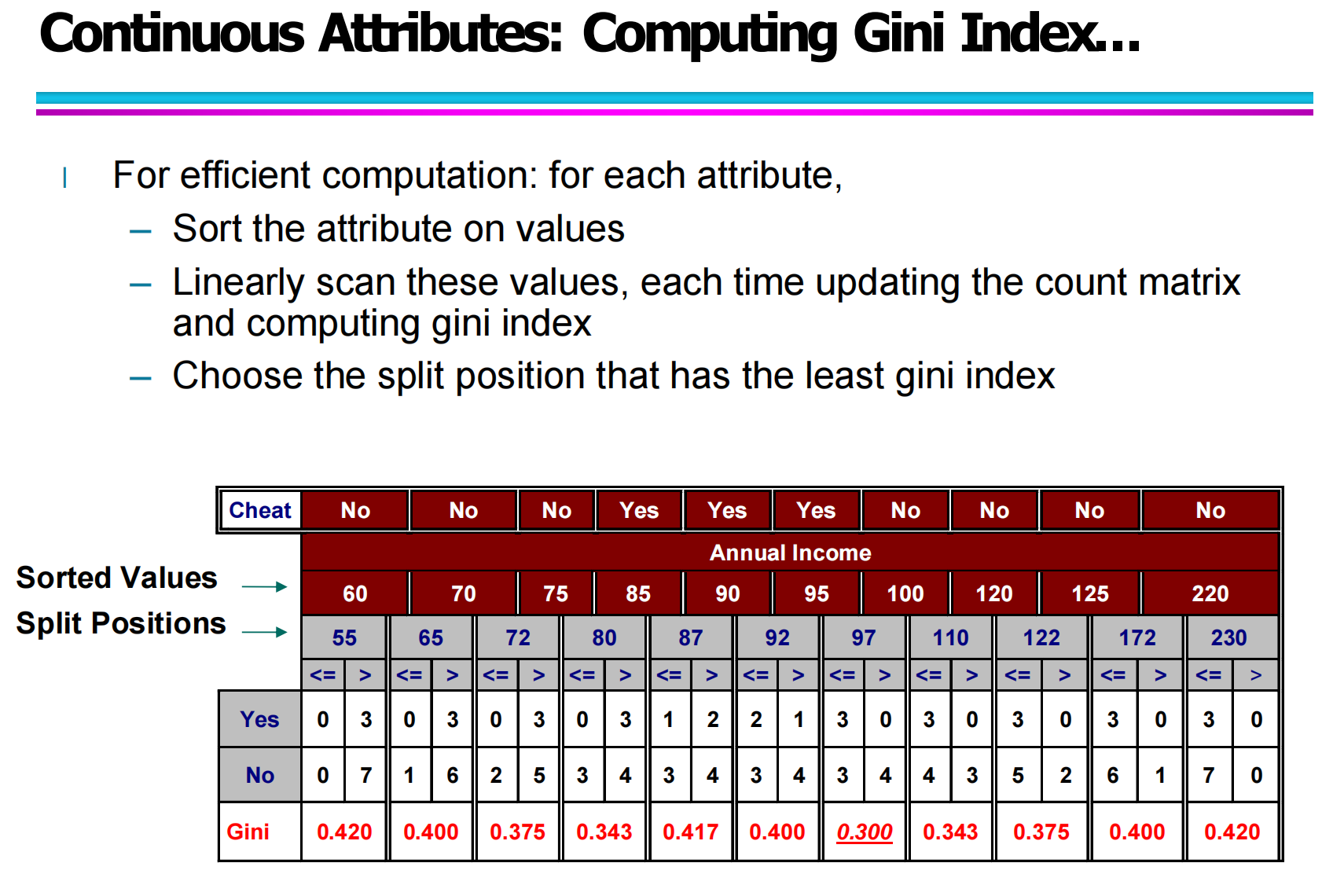
2.3 连续属性:Continuous Attribute 的 Gini 分裂
当属性是连续数值型(例如:Annual Income),不能直接列出所有类别,而是需要选择一个划分点 v,将数据分为:
A ≤ v
A > v
问题关键就是:v 取哪个值最好?
你的图片给出了标准流程:
取出该属性的所有数值并排序。
在排序后的相邻值之间取中点,作为候选分裂点。
对每个候选 v:
分别统计左右两侧的类别分布
计算左右 Gini
再计算加权 Gini
最终选取 Gini 最小的那个分裂点。
虽然这种方法直观,但如果数据量很大,逐个枚举会非常耗时,因此后面又引出“高效计算”的方法。

2.4 连续属性的高效计算方法
对于连续属性的 Gini 计算,如果每个候选点都完整重新计算,是非常低效的。
更好的方法是:
先排序属性值
线性扫描排序后的样本
每移动一个位置,只更新左右两边的类别计数
动态维护当前 Gini
这样复杂度从“每次重算”降为“线性更新”,效率显著提高。
图中红色标出的 0.300,表示在该划分点处 Gini 最小,是当前属性的最优划分点。
三、Gini指数实例详解(Gini Index Examples)
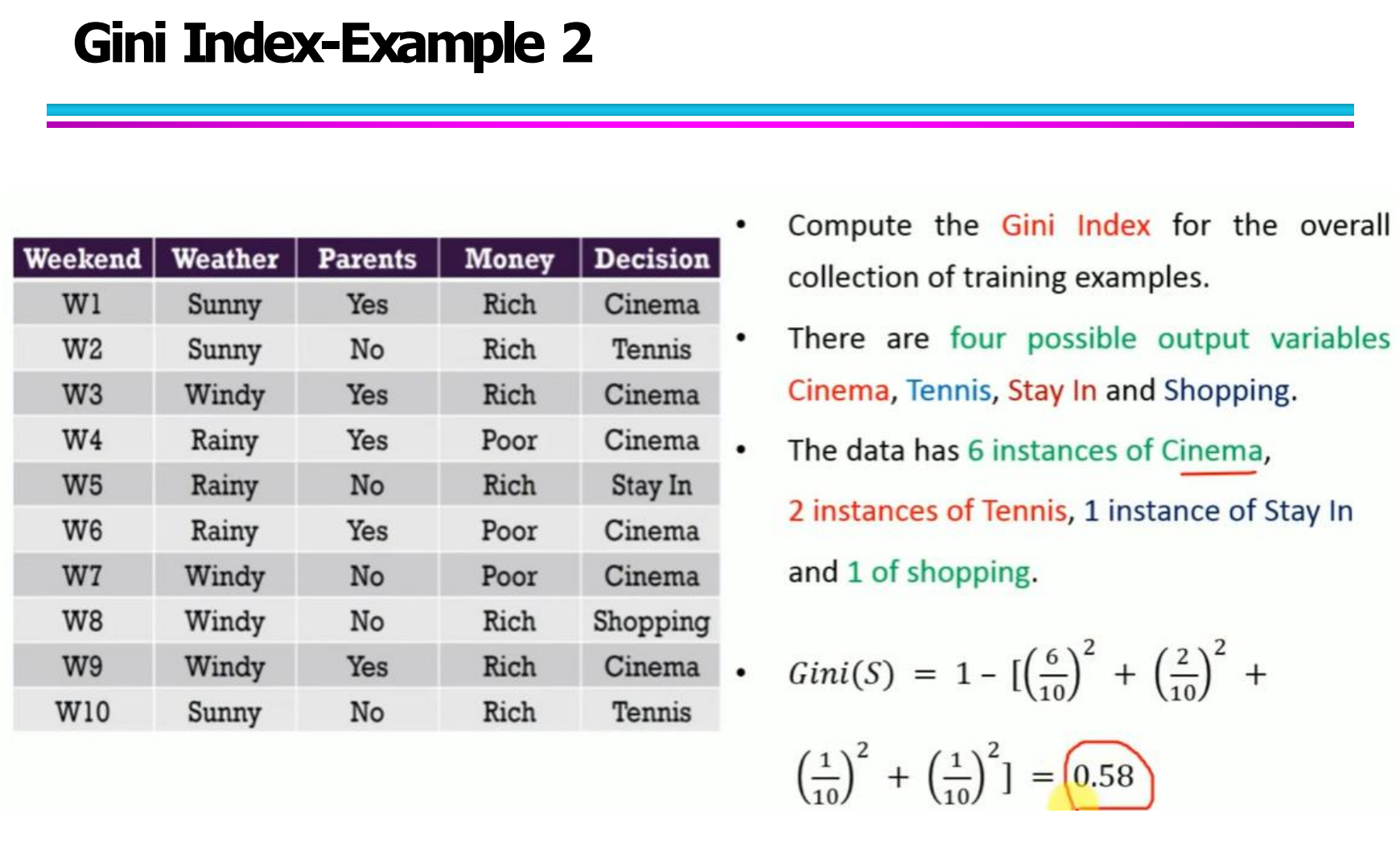
3.1 数据集说明(Dataset Description)
我们使用一个包含 10 条记录的 Weekend 决策数据集,每条记录由以下属性组成:
Weekend:周末编号(W1 – W10)
Weather:天气情况(Sunny / Rainy / Windy)
Parents:父母是否同行(Yes / No)
Money:金钱状态(Rich / Poor)
Decision:最终决策结果(Cinema / Tennis / Stay In / Shopping)
这个数据集的目标是:
根据前三个特征(Weather, Parents, Money),预测用户最终的 Decision。
3.2 整体数据集的 Gini 指数计算(Overall Gini Index)
首先,计算整个数据集的 Gini Index。
数据集中一共有 10 条记录,决策结果的类别分布如下:
Cinema:6 个
Tennis:2 个
Stay In:1 个
Shopping:1 个
按照 Gini 公式:
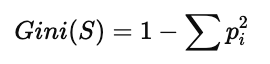
代入数据:
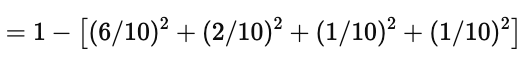
最终得到:
Gini(S) = 0.58
说明当前数据集具有较高的不纯度,需要进一步划分。
3.3 基于 Money 属性的 Gini 计算(Gini for Money Attribute)
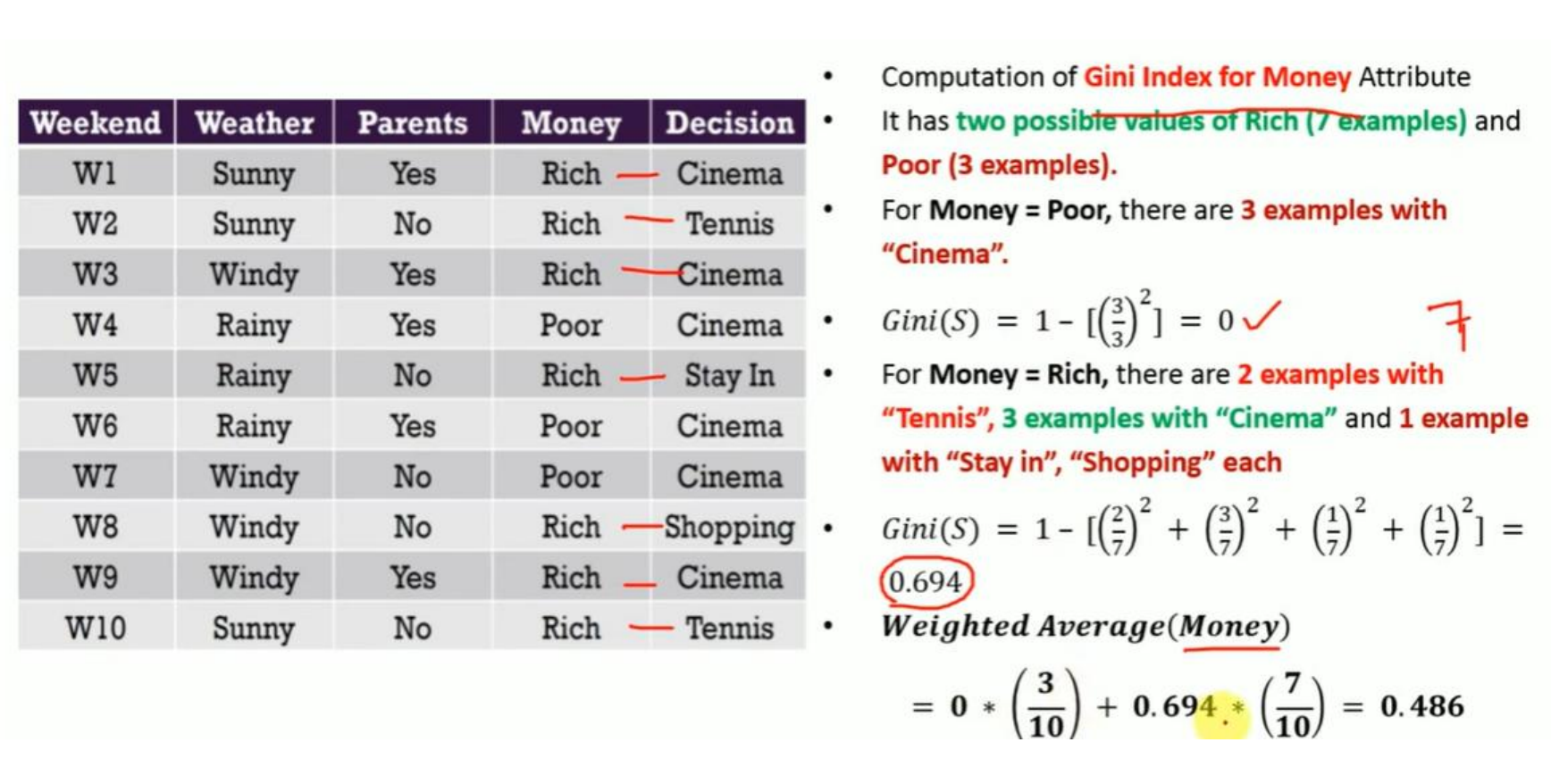
Money 有两个取值:
Rich(7个样本)
Poor(3个样本)
(1)Money = Poor 子集
子集中 3 条记录:
全部是 Cinema
因此:
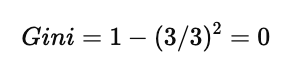
该子集是 完全纯的。
(2)Money = Rich 子集
子集中共有 7 条数据:
Cinema:3
Tennis:2
Stay In:1
Shopping:1
代入公式:
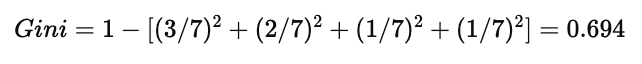
(3)加权 Gini(Weighted Gini for Money)
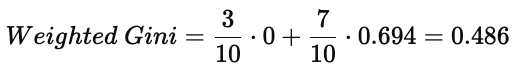
所以:
Money 属性的 Gini Index = 0.486
3.4 基于 Parents 属性的 Gini 计算(Gini for Parents Attribute)

Parents 有两个取值:
Yes:5 个样本
No:5 个样本
(1)Parents = Yes 子集
5 条数据中:
全部是 Cinema
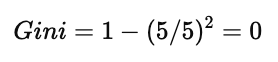
是一个 完全纯节点。
(2)Parents = No 子集
5 条数据中:
Tennis:2
Stay In:1
Shopping:1
Cinema:1
计算:
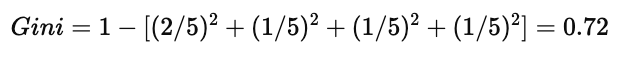
(3)加权 Gini(Weighted Gini for Parents)
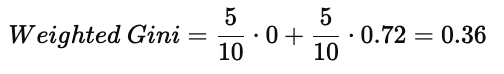
所以:
Parents 属性的 Gini Index = 0.36
3.5 基于 Weather 属性的 Gini 计算(Gini for Weather Attribute)
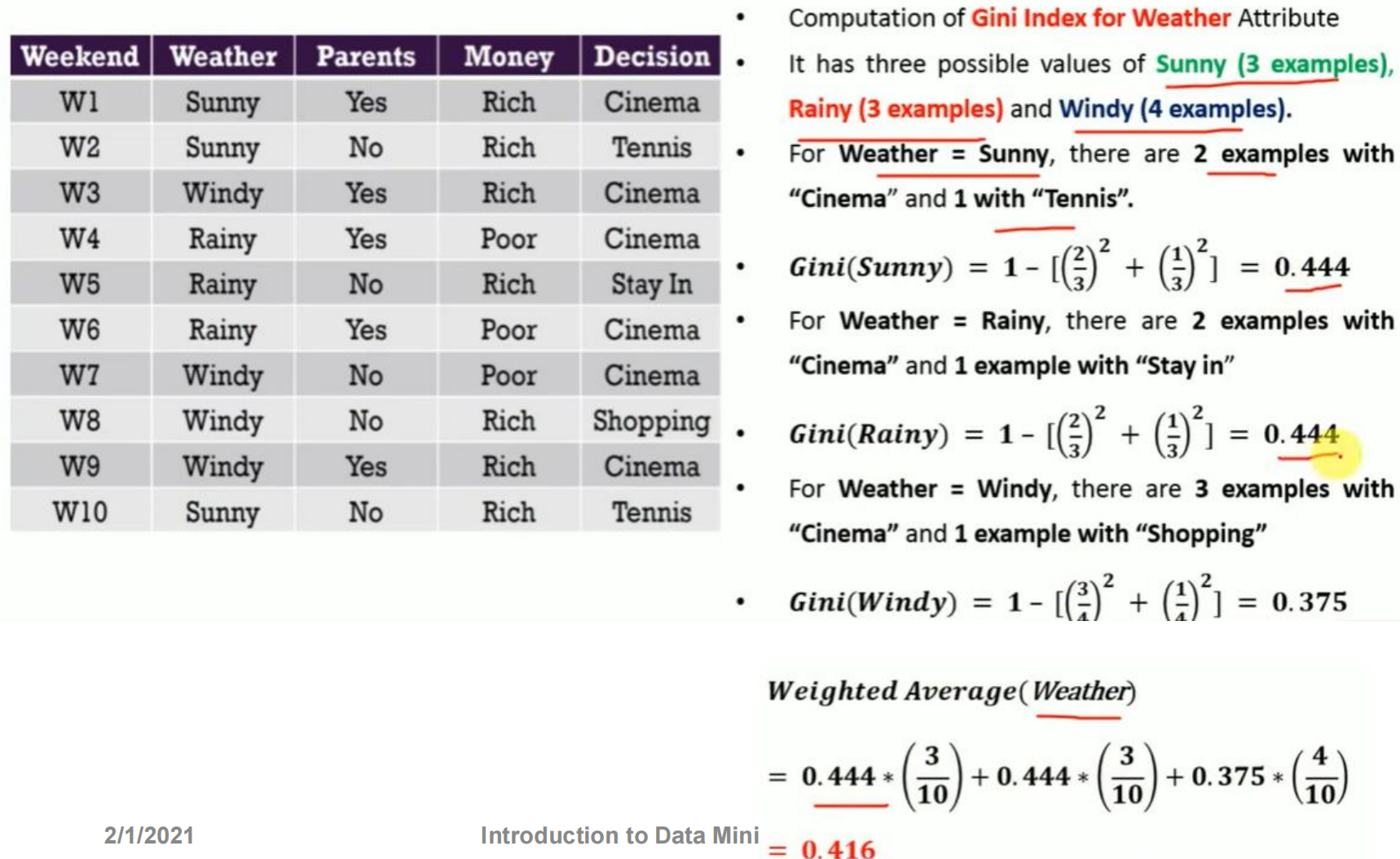
Weather 有 3 个取值:
Sunny:3 个样本
Rainy:3 个样本
Windy:4 个样本
(1)Weather = Sunny
Cinema:2
Tennis:1
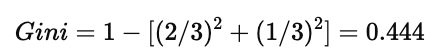
(2)Weather = Rainy
Cinema:2
Stay In:1
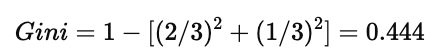
(3)Weather = Windy
Cinema:3
Shopping:1
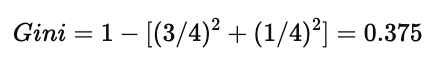
(4)加权 Gini(Weighted Gini for Weather)

所以:
Weather 属性的 Gini Index = 0.416
3.6 最优划分属性选择(Best Split Attribute Selection)

比较三个属性的 Gini 值:
因为:
Parents 拥有最小的 Gini Index,所以被选为根节点(Root Node)。
这说明:
按照 Parents 这个属性进行第一次划分,可以使数据集拥有最高的纯度提升。
四、基于 Gini 的后续划分与完整决策树构造
通过前几章,我们已经得到一个很明确的结论:
在根节点中,Parents 的 Gini Index 最小,因此被选作根节点进行第一次划分。
Parents → Yes / No 两个分支
4.1 Parents = Yes 分支:直接成为叶节点
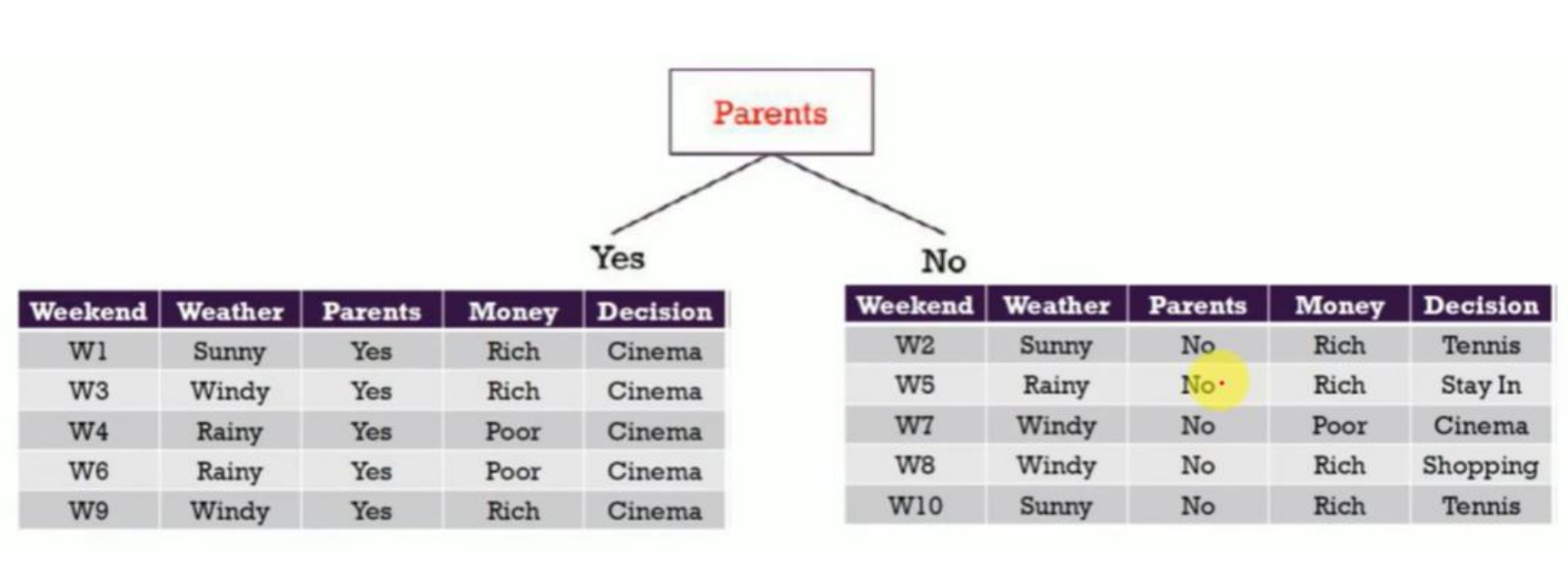
从图中左侧那部分可以看到:
当 Parents = Yes 时,数据子集是:
W1、W3、W4、W6、W9
对应的 Decision 全部是 Cinema,也就是说这一部分数据的类别已经是完全纯净的。
所以这里有两个重要点:
纯节点的 Gini = 0
不需要再继续划分
因此可以直接生成一个叶节点:
Parents = Yes → Decision = Cinema(叶节点)
这是一个非常理想的分支,因为一步就完成了分类。
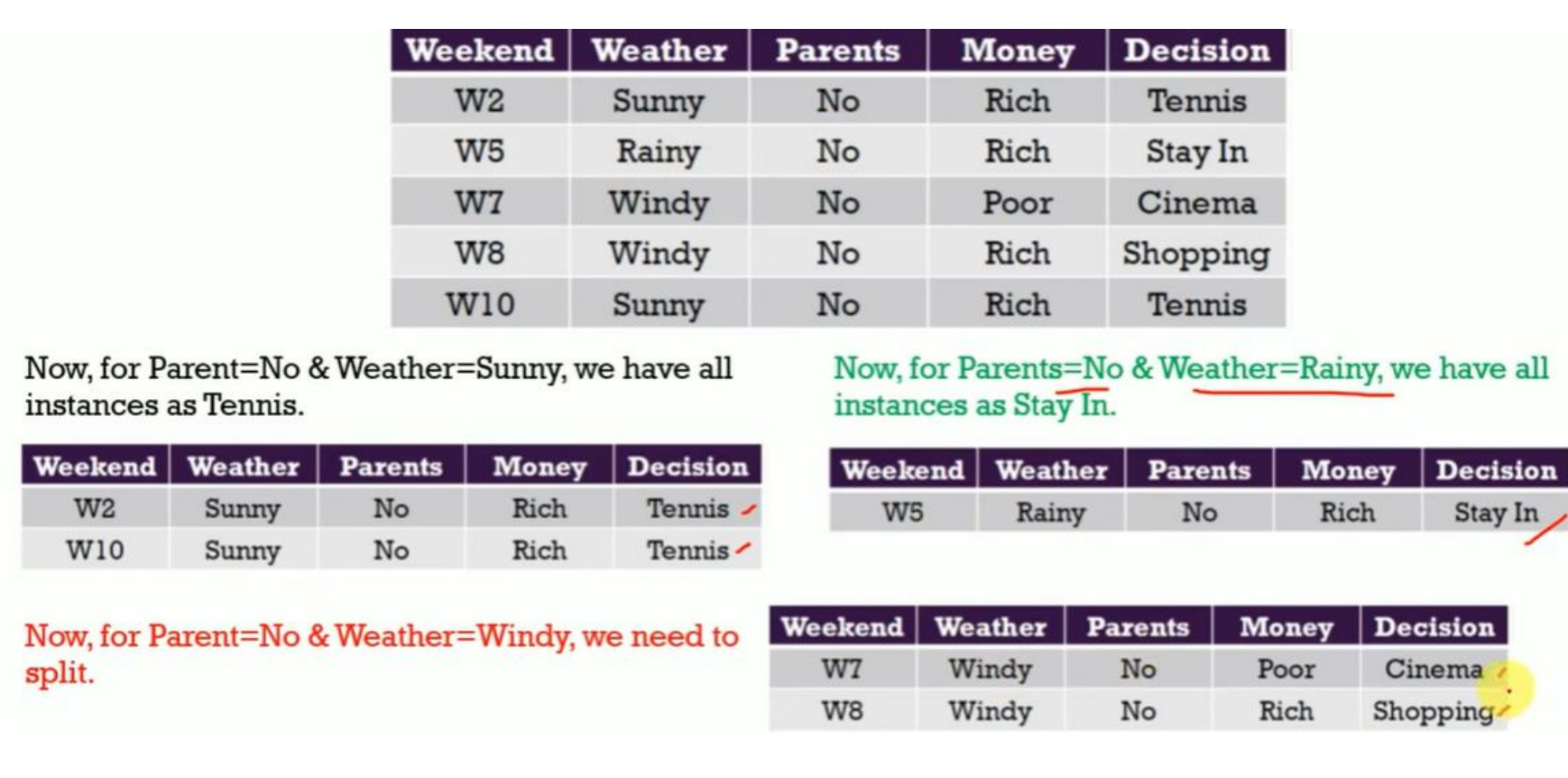
4.2 Parents = No 分支:仍需继续划分
接着图中右侧部分,也就是:
Parents = No 的子集:
这里的类别显然是混合的:
有 Tennis / Stay In / Cinema / Shopping,因此必须继续划分。
4.3 在 Parents = No 条件下选择下一个最优属性
计算了在 Parents = No 条件下:
用 Weather 再次划分

用 Money 再次划分


并计算对应的 Gini Index。
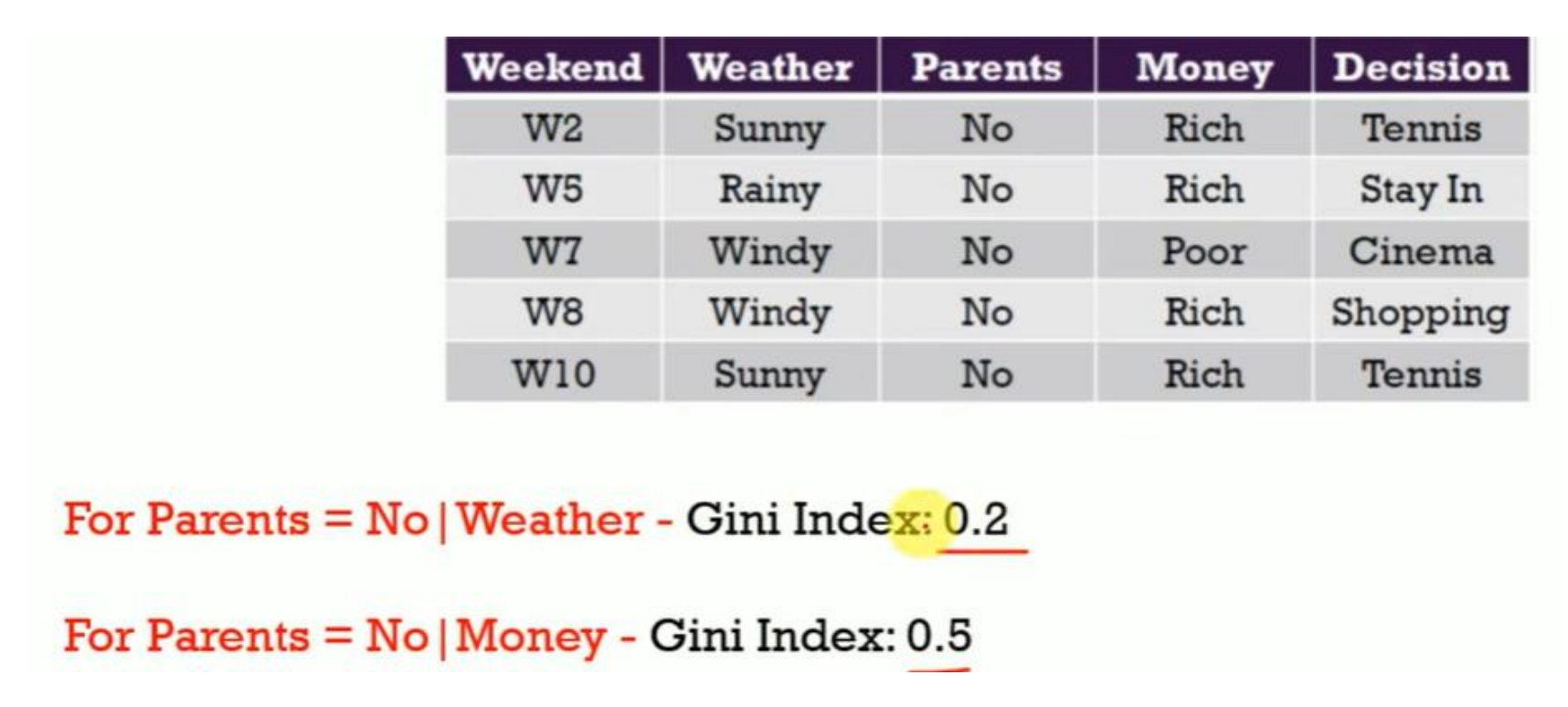
最后给出的结果是:
Parents = No | Weather → Gini = 0.2 ✅
Parents = No | Money → Gini = 0.5
所以结论非常清楚:
在 Parents = No 这个子节点中,下一步最优划分属性是:Weather
五、Gini指数实例详解2(Gini Index Examples 2)