一、放回抽样的定义

放回抽样是一种统计学中的抽样方法,其中每次从总体中抽取一个样本后,该样本会被放回总体中,使得每次抽取都是独立的。这种方法确保了总体中的每个样本在每次抽取时都有相同的机会被选中。
这幅图片直观地展示了放回抽样的过程。图片顶部显示了一组不同颜色的圆柱体,代表总体中的不同“标记”或“令牌”。这些标记包括红色、黄色、绿色和蓝色。在“放回抽样”部分,可以看到从这组标记中抽取了一些样本,并且每次抽取后,样本都被放回,因此相同的标记可能会被多次抽取。例如,绿色和蓝色的标记在样本中多次出现,展示了即使某个标记已经被抽取过一次,它仍然有可能在后续的抽取中再次被选中。这种抽样方式在随机森林算法中非常有用,因为它允许每个决策树从特征集中随机选择特征,从而增加模型的多样性和鲁棒性。
例子
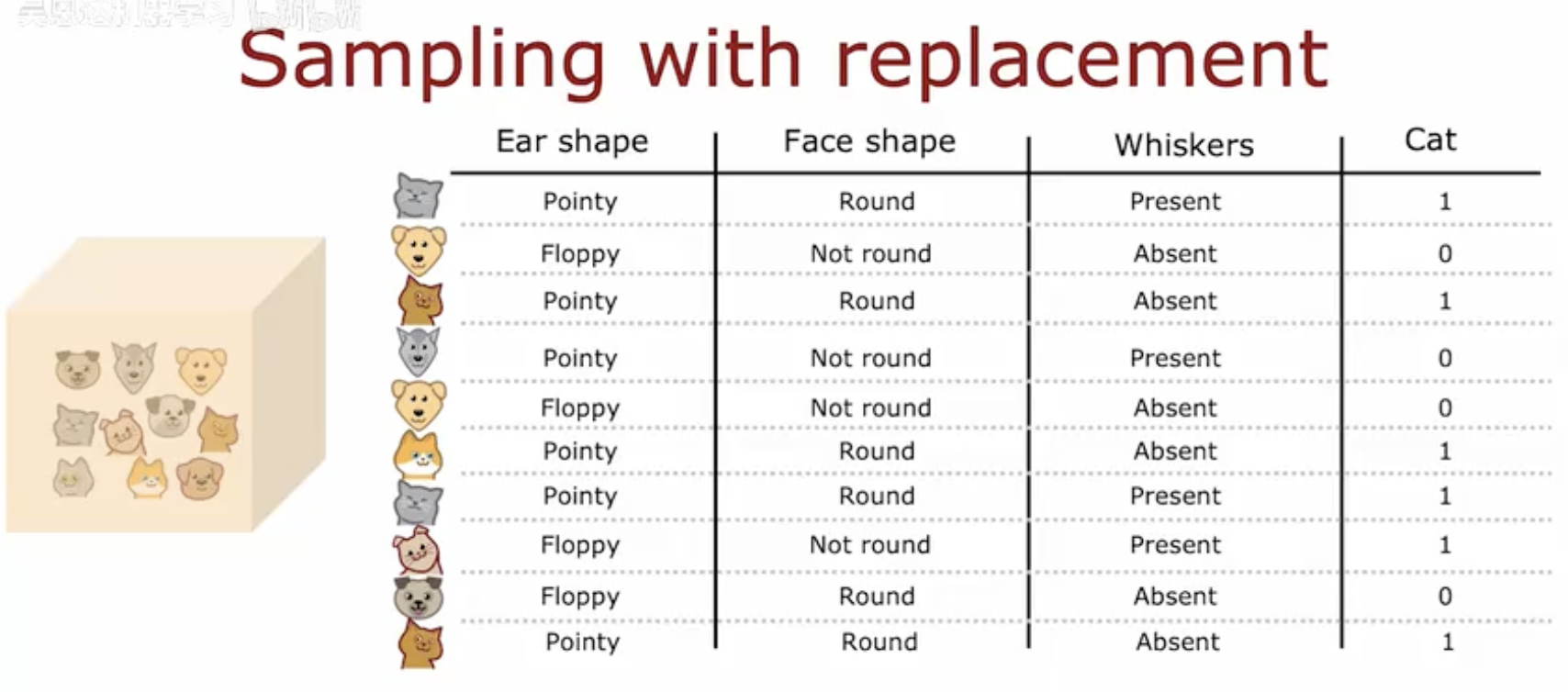
这幅图片展示了一个关于放回抽样的示例,具体用于分类猫的特征。图片左侧显示了一组猫的图像,右侧是一个表格,列出了猫的不同特征及其对应的分类结果。
表格包含以下列:
Ear shape(耳朵形状):分为“Pointy(尖的)”和“Floppy(圆的)”。
Face shape(脸型):分为“Round(圆的)”和“Not round(不圆的)”。
Whiskers(胡须):分为“Present(有)”和“Absent(无)”。
Cat(猫):表示该特征组合是否属于猫,用1表示是猫,0表示不是猫。
表格中的每一行代表一个猫的特征组合,例如:
第一行:尖耳朵、圆脸、有胡须,被分类为猫(1)。
第二行:圆耳朵、不圆脸、无胡须,被分类为不是猫(0)。
放回抽样在这里指的是,每次抽取一个特征组合后,该组合会被放回,因此在后续的抽取中可以再次被选中。这种抽样方式使得相同的特征组合可以重复出现。
总结来说,这幅图片通过一个具体的例子展示了放回抽样的概念,即在抽取样本时,每次抽取后将样本放回,使得相同的样本可以被多次抽取。
二、随机森林算法的定义
随机森林算法是一种集成学习方法,它通过构建多个决策树并将它们的预测结果进行汇总来提高模型的预测准确性和稳定性。每棵决策树都是在数据的一个随机子集上训练得到的,这样可以增加模型的多样性,减少过拟合的风险。
通俗理解:
随机森林就像是一个由很多专家组成的团队,每个专家(决策树)都独立地对问题给出自己的意见,然后通过投票或平均的方式来决定最终的答案。这种方法往往比单个专家(单一决策树)更可靠,因为它综合了多方的意见,减少了单一意见可能带来的偏差。
例子

这幅图片展示了如何生成随机森林中的树样本。具体步骤如下:
给定训练集:首先有一个大小为 m 的训练集。
重复抽样:对于 b=1 到 B(B 是树的数量),进行以下操作:
使用放回抽样创建一个新的大小为 m 的训练集。
训练决策树:在新的数据集上训练一个决策树。
图片中展示了两个决策树的结构:
左边的树首先根据胡须(Whiskers)的存在与否进行分裂,然后根据耳朵形状(Ear shape)和脸型(Face shape)进一步分裂。
右边的树首先根据耳朵形状(Ear shape)进行分裂,然后根据脸型(Face shape)进一步分裂。
这些树是通过放回抽样生成的,因此每个树的训练数据可能包含重复的样本。这种方法有助于减少模型的方差,提高模型的泛化能力。
三、随机森林中的特征随机选择策略

这幅图片解释了随机森林算法中特征选择的随机化过程。
标题:图片的标题是“Randomizing the feature choice”,意思是“随机化特征选择”。
描述:图片中的文字说明了在随机森林算法中,每当在决策树的每个节点选择一个特征进行分裂时,如果总共有 n 个特征可用,算法会随机选择一个包含 k 个特征的子集,其中 k<n。然后,算法只从这个随机选择的特征子集中选择特征来进行分裂。
公式:图片中给出了一个常见的选择 k 的公式,即 k=根号n。这意味着在特征选择时,通常选择的特征数量是总特征数量的平方根。这个公式是一个经验法则,用于在随机森林中平衡模型的多样性和性能。
总结来说,这幅图片描述了随机森林算法中一个关键的随机化步骤,即在每个决策节点上,不是考虑所有特征,而是只从随机选择的一小部分特征中选择最佳特征进行分裂,以此来增加模型的多样性和减少过拟合的风险。
