一、引言

在数据挖掘与机器学习领域中,预测建模(Predictive Modeling) 是最核心的任务之一。它的目标是利用历史数据,建立数学模型,对未知或未来的结果进行预测。而在预测建模的范畴下,最常见的两类问题便是——回归(Regression)与分类(Classification)。
这两种方法虽然在算法形式上可能类似(都通过学习输入特征与输出结果之间的映射关系),但预测目标和应用场景却有本质的不同。回归任务关注的是连续数值的预测,例如预测房价、温度、销售额等;而分类任务则处理离散类别的问题,例如判断邮件是否为垃圾邮件、预测客户是否会违约等。
如上图所示,分类问题的输出结果通常是预定义的几个类别,而回归问题的输出是一个可变的连续值。虽然两者的任务不同,但它们都在建模输入变量与输出结果之间的依赖关系,只不过预测的目标性质不同。
在整个机器学习体系中,回归和分类是监督学习(Supervised Learning)的两大支柱。理解它们的差异不仅是学习算法的基础,也是选择合适模型、正确评估预测效果的关键步骤。
二、回归与分类的基本区别
在监督学习(Supervised Learning)中,所有预测任务大体可以分为两类:回归(Regression)和分类(Classification)。这两种任务虽然都通过已有样本学习输入与输出之间的映射关系,但它们的预测目标与结果形式存在本质差异。
回归任务的输出是一个连续的数值。模型的目标是尽可能逼近真实值,例如预测房价、气温、销售额、股票价格等。数学上,回归模型学习的是一个连续函数关系:

其中 y 是预测值,x 是输入特征,ε 是噪声项。模型通过最小化误差(如均方误差 MSE)来提升预测精度。
与之相对的,分类任务的输出是一个离散的类别标签。模型的目标不是预测具体数值,而是判断样本属于哪一类。例如判断邮件是否为垃圾邮件、病人是否患病、客户是否会违约等。分类模型更关注“边界”的划分,它要学习的是决策面(Decision Boundary),使不同类别的数据被有效区分开来。

上图展示了两者在输出形式上的差异。回归任务的输出值可以取任意实数,因此在坐标图中表现为一条连续曲线;而分类任务则将数据划分为若干区域,每个区域代表一个固定类别。
为了更直观地理解二者的区别,我们可以通过“天气温度预测”这一例子来说明:
若问题是“明天的气温是多少华氏度?”,这是一个回归问题。模型会输出一个具体的温度值,如 84°F。
若问题是“明天是炎热的还是寒冷的?”,则是一个分类问题。模型输出一个类别标签,如 “Hot” 或 “Cold”。
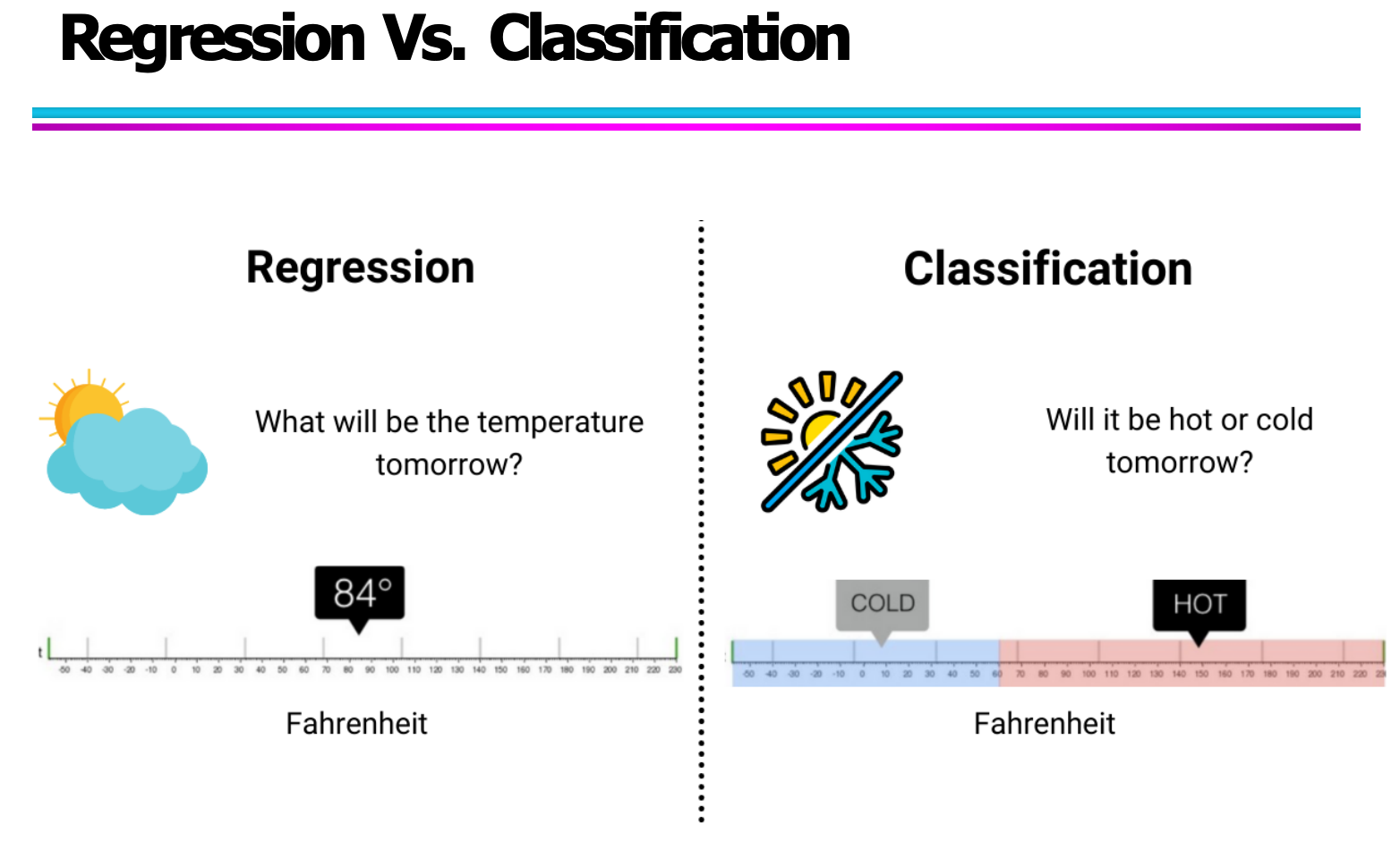
如上图所示,回归模型在数轴上预测的是连续位置,而分类模型则通过设定阈值,将温度划分为不同区间对应的类别。前者追求“值的接近”,后者追求“类的正确”。
此外,二者的评估方式也不同:
回归模型通常使用 均方误差(MSE)、平均绝对误差(MAE) 来衡量预测值与真实值的偏差;
分类模型则使用 准确率(Accuracy)、精确率(Precision)、召回率(Recall) 等指标来评估分类的正确性。
综上所述,回归与分类的主要区别可以概括为:
无论是预测价格还是判断类别,这两种任务都构成了数据挖掘的基础。它们相辅相成,共同构建了监督学习的核心框架。
三、实际应用场景
回归与分类是机器学习和数据挖掘中最常见、最具代表性的两类任务,它们在不同领域中发挥着关键作用。理解它们的应用场景,有助于在实际问题中选择合适的建模方法。
1. 回归任务的典型应用
(1)价格与市场预测
在经济与商业领域,回归分析被广泛用于预测连续数值。例如房价预测模型会综合地段、面积、装修情况、学区等因素来估算房屋价格;电商平台通过回归模型预测商品销量,以调整库存与广告投放策略。
(2)金融与投资分析
在金融市场中,回归模型可用于预测股票价格走势、汇率波动或债券收益率。线性回归、时间序列回归和LSTM等模型都常被用于建立量化交易策略。
(3)工业与科学研究
在工程领域中,回归模型可用于预测温度、压力、能耗等连续指标;在医学研究中,也常用回归分析研究药物剂量与疗效的关系。
2. 分类任务的典型应用
(1)风险识别与信用评估
银行和保险公司利用分类模型(如逻辑回归、决策树)来判断客户是否具有违约风险。模型输出“高风险”或“低风险”标签,为信贷审批提供依据。
(2)垃圾邮件过滤与内容审核
电子邮件系统利用文本分类模型对邮件内容进行判断,将其划分为“正常邮件”或“垃圾邮件”;同样的思路也应用于社交平台的内容审核系统。
(3)医疗诊断与疾病预测
在医疗领域中,分类算法可用于识别患者是否患有特定疾病。例如通过生理指标判断糖尿病风险,或根据X光图像判别肺部病变。
(4)计算机视觉与语音识别
图像识别任务中,模型要将图片分类到正确的标签,如“猫”“狗”“汽车”等;语音识别中,分类算法用于将声音信号转化为文字。
四、方法与模型
(1)线性回归(Linear Regression)
线性回归是最基础也是最经典的回归方法,它假设输入特征与输出结果之间存在线性关系。模型通过最小化均方误差(MSE)来优化参数,形式简单、可解释性强。
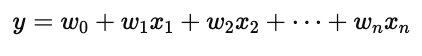
尽管它无法处理复杂的非线性关系,但在经济预测、实验分析等场景中仍被广泛使用。
(2)多项式回归(Polynomial Regression)
为了解决非线性问题,可以引入高次项,使模型能拟合更复杂的曲线。但高次多项式容易导致过拟合,因此需要正则化方法(如岭回归 Ridge Regression 或套索回归 Lasso Regression)来控制复杂度。
(3)树模型与集成方法(Tree-based Models)
决策树(Decision Tree)、随机森林(Random Forest)和梯度提升树(Gradient Boosting Tree, GBDT)等方法在回归任务中同样有效。它们无需假设线性关系,能自动捕捉特征间的非线性依赖,尤其适合结构化数据。
(4)神经网络回归(Neural Network Regression)
在复杂场景(如图像回归或时序预测)中,可以使用深度神经网络,通过多层非线性变换学习复杂的映射关系。
2. 分类模型(Classification Models)
(1)逻辑回归(Logistic Regression)
尽管名字中带有“回归”,但逻辑回归本质上是一个分类模型。它通过Sigmoid函数将线性组合映射为概率值,从而实现二分类任务。该模型计算简单,具有良好的可解释性,是风险评估、广告点击率预测等任务中的常用算法。
(2)决策树与随机森林(Decision Tree & Random Forest)
决策树根据特征划分数据,不仅直观易懂,还能处理非线性关系。随机森林则通过集成多棵决策树,显著提高了模型的稳定性与泛化能力。
(3)支持向量机(Support Vector Machine, SVM)
SVM通过寻找最大化类别间隔的超平面实现分类,尤其适用于中小规模、特征较多的数据集。它在图像识别、文本分类等任务中表现出色。
(4)神经网络与深度学习(Neural Networks & Deep Learning)
对于复杂的高维数据,神经网络能够自动学习特征表示。例如CNN可用于图像分类,RNN与Transformer则在语音与文本分类任务中广泛应用。
五、总结
回归(Regression)与分类(Classification)是监督学习中最核心的两类任务,它们几乎构成了所有预测型机器学习问题的基础。从本质上讲,这两者的区别在于——回归预测连续值,而分类预测离散类别。前者回答的是“是多少”,后者回答的是“属于哪类”。
在前面的章节中,我们从定义、直观示例、应用场景和算法模型等方面系统地分析了两者的差异与联系。
回归模型通过拟合数值关系来预测趋势或结果,如价格、温度、销量等;
分类模型则通过学习决策边界来判断类别,如垃圾邮件识别、疾病诊断、风险判断等。
尽管两种任务在输出目标上不同,但它们共享相似的数学思想与优化逻辑。无论是线性模型、树模型还是神经网络,核心目的都是从历史数据中学习模式,并将其应用于未知样本的预测之中。
从应用层面来看,回归与分类并不是互斥的。许多复杂任务往往需要二者结合使用。例如在信用评分系统中,回归可以预测违约概率,而分类模型则可根据概率阈值判断客户是否属于高风险群体。二者的配合让模型既具备数值解释性,又具备分类决策能力。
未来,随着数据量与计算能力的持续提升,回归与分类算法正在逐步向更智能的方向演进:
一方面,模型正在从传统的线性形式走向深度学习与自适应非线性结构;
另一方面,研究者也在追求模型的可解释性与公平性,使预测不仅准确,而且可信。
总而言之,回归与分类的对比不仅是算法的区分,更是理解机器学习思想的起点。掌握两者的本质区别,意味着具备了处理绝大多数监督学习问题的能力,也为深入研究更复杂的模型奠定了坚实的基础。
