一、熵的直观理解与基本概念

1.1 什么是熵？

在信息论中，熵（Entropy）用来衡量一个随机变量的不确定性大小。简单理解：
一个系统越“混乱”、越难预测，它的熵就越大；
一个系统越“有序”、结果越确定，它的熵就越小。

比如：

• 如果抛一枚均匀的硬币，正反两面出现的概率各是 0.5，这时结果很难预测，熵比较大。

• 如果这枚硬币被动过手脚，抛出去几乎每次都是正面，那么结果几乎确定，熵就非常小，甚至接近 0。

从本质上看，熵描述的是：平均需要多少比特的信息，才能描述一个事件的结果。

1.2 熵的数学定义

设随机变量为 X，有 n 种可能取值：

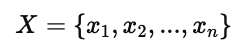
每个结果的概率为：

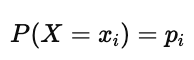
那么熵定义为：

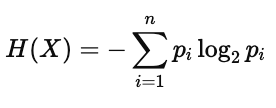
其中：

• p_i：事件发生的概率

• log⁡₂：以 2 为底的对数，单位是 bit（比特）

• 熵的取值范围是：

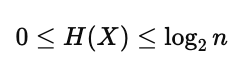
当所有事件等概率发生时，熵达到最大。

1.3 抛硬币例子：直观理解熵

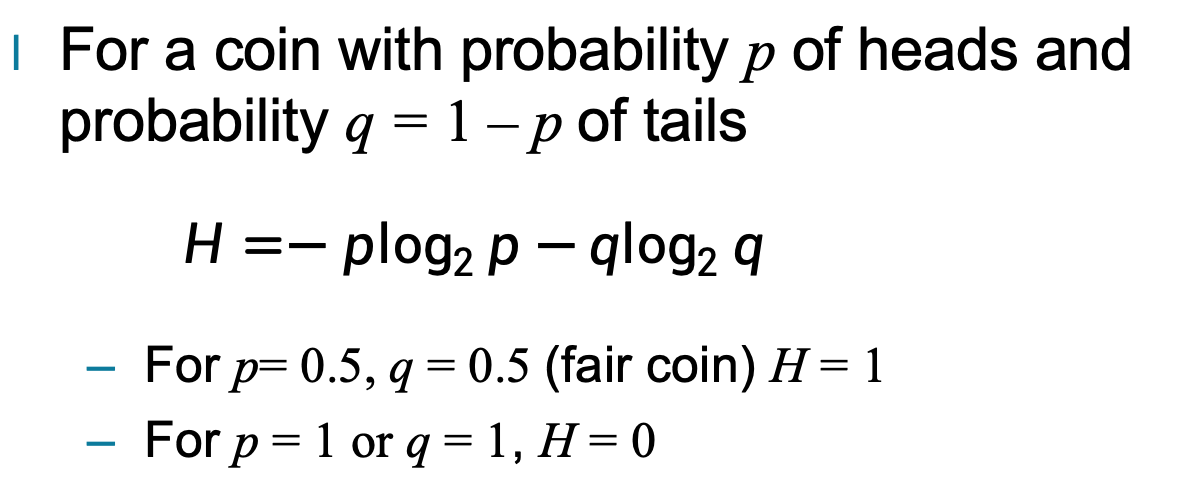
如果一枚硬币，正面概率为 p，反面概率为 q=1−p，
那么熵为：

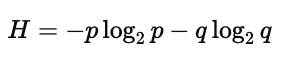
特殊情况：

• 当 p=0.5，此时最随机，熵最大：

• 当 p=1 或 p=0，结果完全确定：

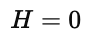
也就是说：
越接近“均匀分布”，熵越大；
越接近“确定结果”，熵越小。

二、最大熵与样本熵计算

在第一章中，我们已经介绍了熵的基本概念以及它在刻画“不确定性”中的核心作用。本章将进一步从最大熵思想和样本数据中的熵计算两个角度展开，帮助你理解熵不仅是一个公式，更是一种非常重要的分布判断准则。

2.1 最大熵原理（Maximum Entropy）

在所有可能的概率分布中，如果一个分布是完全均匀的，也就是每个结果出现的概率都相同，那么它的不确定性是最大的，这时对应的熵也达到最大值。
这是熵理论中的一个重要结论：当概率分布越平均，熵就越大；当某些结果概率明显更高，熵就会下降。

最大熵的数学形式可以表示为：

若一个变量 X 有 n 个可能结果，且概率均相等，即
p₁=p₂=...=p_n=1​/n
则最大熵为：

H_max(X)=log_⁡2(n)

这个结论在很多领域都有应用，例如机器学习中的特征选择、语言模型中的概率建模等。

2.2 离散样本数据中的熵计算示例

在真实数据分析中，我们面对的往往不是理想的均匀分布，而是来自样本数据的统计结果。
此时，熵的计算需要根据每一类所占的比例进行加权求和，其公式为：

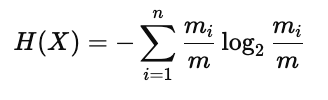
其中：

• m：总样本数

• m_i​：第 ii 类样本数量

• n：不同类别的个数

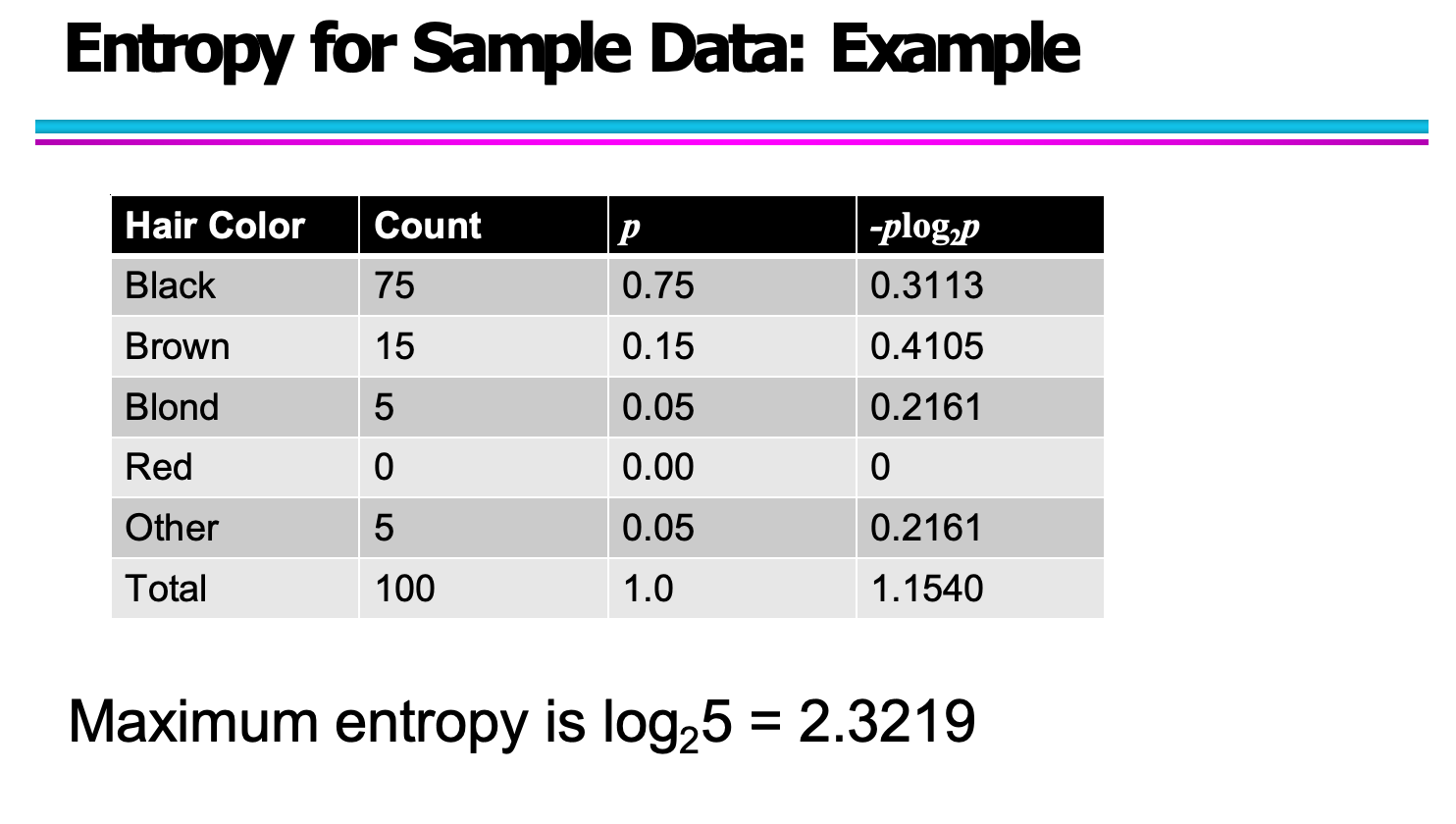
你给出的示例是对头发颜色分布的样本数据进行熵计算。其中统计结果如下：

• Black：75

• Brown：15

• Blond：5

• Red：0

• Other：5

• 总数：100

通过代入公式，可以得到：

同时，该样本的理论最大熵为：

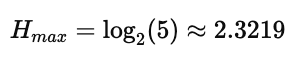
由于当前分布非常不均匀（黑发比例远大于其他颜色），所以实际熵远小于最大熵。

2.3 样本熵的一般计算形式

上面的例子虽然具体，但本质上遵循的是一个通用公式。
这张图给出了一个更加抽象的表达方式，适用于任意离散分类样本：

如果我们有：

• 总样本数：m

• 分类数：n

• 第 i 类样本数：m_i

那么样本熵计算公式仍然是：

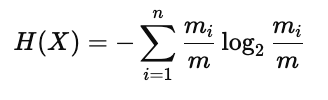
这一定义在决策树构建中尤其重要，因为信息增益的计算就是以这个样本熵为基础。

2.4 样本熵计算完整示例推导

为了让读者更直观理解熵的实际计算方式，可以加入给出的这个“30 名学生头发颜色分布”的案例：

• Black: 10

• Brown: 12

• Blonde: 5

• Red: 3

• 总人数：30

代入公式：

该例子的意义在于：
它展示了如何从一个具体分布出发，一步一步手动推导出熵的值，而不是只停留在公式层面。