一、二元标签简介
在推荐系统中,并不是所有场景都会有用户的明确评分(比如 1 到 5 星)。更多时候,我们只能观察到用户是否产生了某种行为,例如是否点击、是否购买、是否点赞。这类数据往往用 二元标签(Binary labels) 来表示。
所谓二元标签,就是把用户的行为转化为 0/1 的结果:
1 表示用户与物品发生了正向的交互(如点击、购买、喜欢);
0 表示用户没有发生交互;
? 表示该物品尚未展示给用户,因此标签未知。
通俗理解:
这就像一次二选一的问答:用户看见某个物品后,要么“感兴趣” (1),要么“不感兴趣” (0)。推荐系统的目标就是根据已有的观测数据,推断用户对未展示物品的兴趣概率。
二、从评分到二元标签

在传统的推荐系统任务中,用户会对电影、商品等物品打分(如 0–5 星)。但是在很多实际应用场景中,获取到的并不是详细的分数,而是用户是否对物品表现出兴趣。
图中展示了一个例子:
原本 Alice 对《Love at last》打了 5 分,现在被简化为 1(表示喜欢/正向反馈)。
对《Nonstop car chases》打了 0 分,则对应二元标签中的 0(表示不喜欢/负向反馈)。
对于一些没有打过分的电影,标签用 ? 来表示(表示未知,未观测到)。
这种转化的好处是:
把复杂的多等级评分问题简化为“是/否”问题,更加通用。
在点击、购买等场景中,二元标签更符合数据的真实分布。
直观理解:与其让系统预测“用户会给这部电影 4 分还是 5 分”,不如直接预测“用户会不会喜欢/点击这部电影”。这更贴近实际应用。
三、二元标签的应用场景

二元标签在推荐系统和在线平台中非常常见,因为很多时候我们只能观测到用户的行为,而无法得到明确的评分。图中给出了几个典型的应用场景:
购买行为:用户是否在看到商品后完成购买?(是 → 1;否 → 0;未展示 → ?)
点赞/收藏行为:用户是否对某个内容点击“喜欢”或“收藏”?
停留时长:用户是否在某个内容上停留至少 30 秒?(停留足够久可视为感兴趣)
点击行为:用户是否点击了推荐的物品或广告?
在这些场景中,标签的含义是:
1 = 用户产生了交互(engaged),说明有兴趣;
0 = 用户没有交互,说明不感兴趣;
? = 系统还没展示过该物品,因此标签未知。
通俗理解:在电商里,推荐系统会不断尝试“给你看一个商品”,然后观测你是否点击或购买。这种“点或不点”的行为就是二元标签。
四、从回归到二分类

在前面介绍协同过滤时,我们是通过一个线性函数来预测用户对物品的评分:

这相当于一个回归问题,输出可以是任意实数。
但是在 二元标签 的场景中,我们需要预测的是:用户是否会与物品发生交互(1 或 0)。这就要求模型输出的不是一个任意数,而是一个概率值,范围在 0 到 1 之间。
为此,引入 Sigmoid 函数:

这样,预测公式变为:
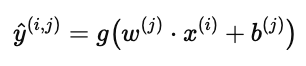
含义是:
当结果接近 1 时,表示用户很可能喜欢或点击该物品。
当结果接近 0 时,表示用户大概率不感兴趣。
通俗理解:之前的模型像是在猜“用户会打几分”,而现在则是在判断“用户会不会点赞/点击”,并给出一个概率,比如“有 80% 的可能点击”。
五、二元标签的代价函数

在二元标签任务中,使用平方误差(如回归任务)并不合适,因为它无法很好地处理概率输出。为此,我们通常采用 对数损失函数(Logistic Loss,也称 Log Loss 或 Cross-Entropy Loss)。
(1)单个样本的损失函数
如果真实标签为 y∈{0,1},预测概率为 y^,则损失函数定义为:
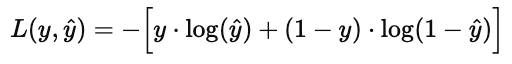
含义:
当真实值 y=1 时,损失为 −log(y^),预测越接近 1 损失越小。
当真实值 y=0 时,损失为 −log(1−y^),预测越接近 0 损失越小。
(2)整体损失函数
对所有用户与物品的观测数据取平均:
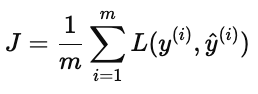
(3)直观理解
如果预测概率与真实结果一致,损失接近 0;
如果预测概率与真实结果差距很大,损失会非常大(被强烈惩罚);
相比平方误差,Log Loss 更适合分类问题,因为它考虑了概率分布的匹配。
通俗来说:Log Loss 就像一个“惩罚函数”,如果你对用户很可能点击的内容预测了一个很低的概率,那就会被狠狠惩罚。
六、总结与应用
在推荐系统中,二元标签是一种非常常见的数据形式。与评分预测不同,它不需要用户明确给出分数,而是通过 行为数据(点击、购买、点赞、停留) 来判断用户的兴趣。这种建模方式将复杂的预测问题简化为 二分类任务。
核心思想:预测用户是否会对某个物品产生兴趣,用概率来衡量。
建模方法:通过 Sigmoid 函数将预测值映射到 [0,1],并使用 Log Loss 衡量预测与真实标签的差距。
优势:适用范围广,特别适合只有“交互/未交互”数据的场景。
典型应用场景:
点击率(CTR)预估:预测广告或推荐内容的点击概率;
购买预测:预测用户是否会下单;
互动预测:预测是否会点赞、评论、转发等。
二元标签方法虽然简单,但却是现代推荐系统、广告投放和信息流排序的核心基础。几乎所有的推荐平台在底层都会使用这一建模方式。
