一、概括
这篇文章主要围绕如何根据数据分布选择合适的特征展开。通过直方图和分布曲线对比,展示了非高斯分布的数据在经过对数、平方根、幂次等数学变换后,能够更接近高斯分布,从而提升模型的表现。文章强调了理解数据特征分布的重要性,并介绍了常见的特征变换方法,为构建更稳健的机器学习模型提供思路。
二、非高斯特征的变化

这幅图片的标题是 “Non-gaussian features”。主要展示了如何通过数学变换把非高斯分布的数据转化为接近高斯分布的形式。
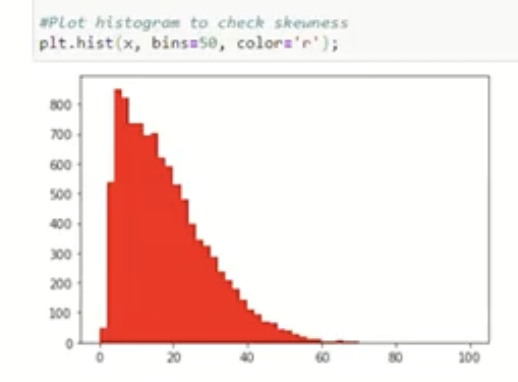
左上角的直方图展示了变量 xx 的分布,图像大致对称但并不完全标准化,红色曲线是其拟合的分布曲线。旁边有公式 p(x1;μ1,σ12),表示高斯分布的概率密度函数。
右侧用蓝色手写公式展示了常见的数据变换方式:
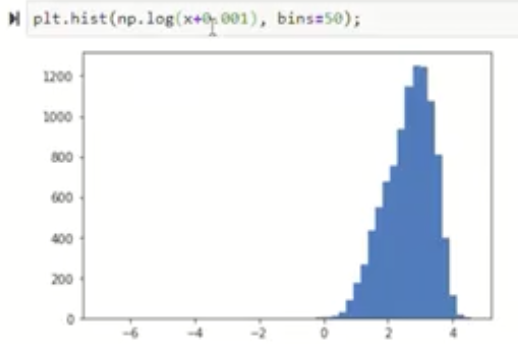
X1←log(X1)
X2←log(X2+1),或者更一般的 log(X2+C)(其中 C 用是常数)
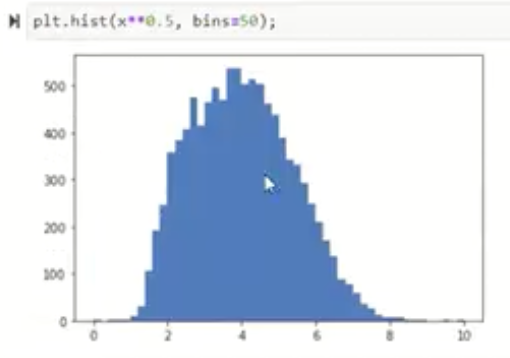
X3←X31/2
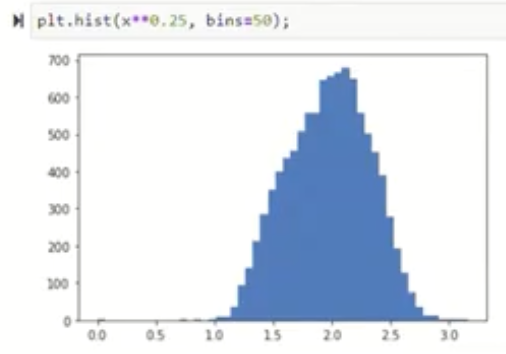
X4←X41/3
左下角的直方图展示了一个偏态分布的例子,横轴是 x,分布在右侧拖尾。箭头指示对该变量做对数变换 log(x)。变换后,右下角的直方图显示分布变得更加对称,接近高斯分布。
整体上,这张图通过原始直方图与变换后的对比,直观地说明了如何使用对数、平方根、幂次等方法把非高斯特征转化为更接近高斯分布的特征。
例子
三、异常检测中的误差分析
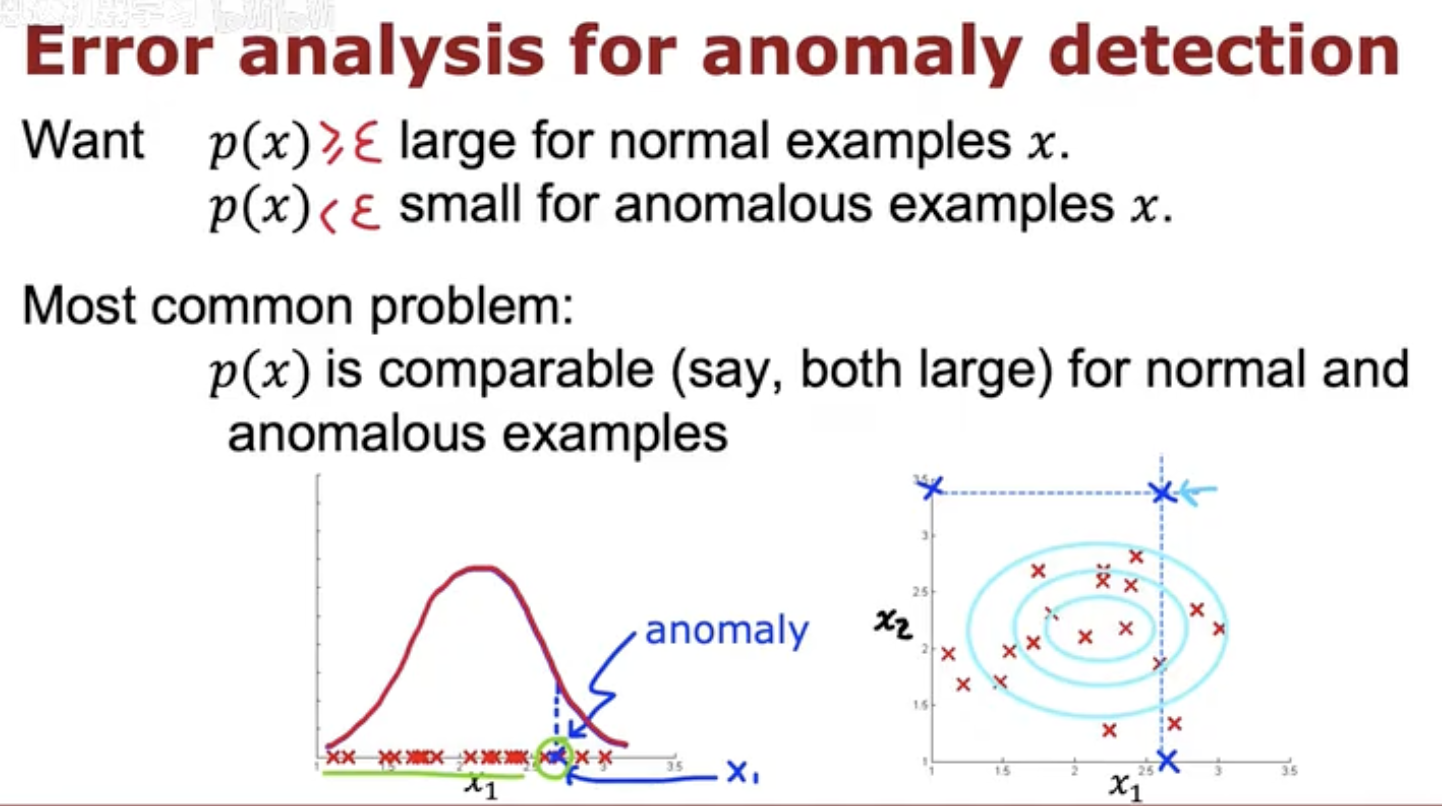
对正常样本,希望 p(x)≥ε 且数值较大;
对异常样本,希望 p(x)<ε 且数值较小。
接着指出了最常见的问题:正常样本与异常样本的概率 p(x) 可能相近(例如都较大),导致难以区分。
左下角的图展示了一维分布,横轴为 x1,红色曲线为分布曲线,图中有很多红色叉号表示样本点。右边圈出一个绿色的点,标注为 “anomaly”,表示虽然概率较大但属于异常样本。
右下角的图是二维情况,横轴为 x1,纵轴为 x2。红色叉号代表数据点,蓝色同心圆表示等概率密度曲线。外围几个蓝色标注的点也被认为可能是异常点。
例子

这幅图片标题为 “Monitoring computers in a data center”,主要展示了在数据中心环境下进行异常检测时可能选择的特征。上方的文字指出,应当挑选那些在异常情况下可能出现异常大或异常小数值的特征。
具体特征定义如下:
x1:计算机的内存使用量
x2:每秒磁盘访问次数
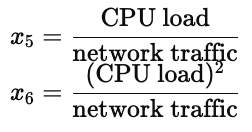
x3:CPU 负载(旁边有蓝色箭头标注)
x4:网络流量(旁边有蓝色箭头标注)
此外,还引入了组合特征:
最后一行说明,特征的选择应当基于概率 p(x),即在正常样本时其值较大,而在交叉验证集中出现异常时,其值会变得较小。
