第一节:机器如何“理解”语义?
在深度学习统治自然语言处理(NLP)之前,计算机看待单词的方式非常简单:每一个词都被视为一个孤立的符号。通常我们使用 One-hot 编码,即给每个词一个极长的向量,其中只有一个位置是 1,其余全是 0。
但这种方法有一个致命的缺陷:它无法表达词与词之间的关系。在 One-hot 空间里,“麦当劳”和“汉堡”的向量是正交的,计算机无法从这些数字中感知到它们在语义上的关联。
1.1 分布式语义假设 (Distributional Semantics)
我们如何定义一个词的含义?现代 NLP 的基石是分布式语义假设:一个词的含义是由它周围经常出现的词决定的。
“You shall know a word by the company it keeps.” —— J.R. Firth (1957)
如果“银行”这个词经常出现在“资金”、“贷款”、“账户”周围,那么这些词汇的集合就定义了“银行”。
1.2 词向量空间与线性直觉
Word2vec 的出现彻底改变了这一点。它不再使用稀疏的 One-hot 编码,而是将每个词映射到一个低维、稠密的连续向量空间中(通常是 50 到 300 维)。
在这个空间里,语义相近的词在几何距离上更接近。更神奇的是,这个空间具备线性代数运算的特性。
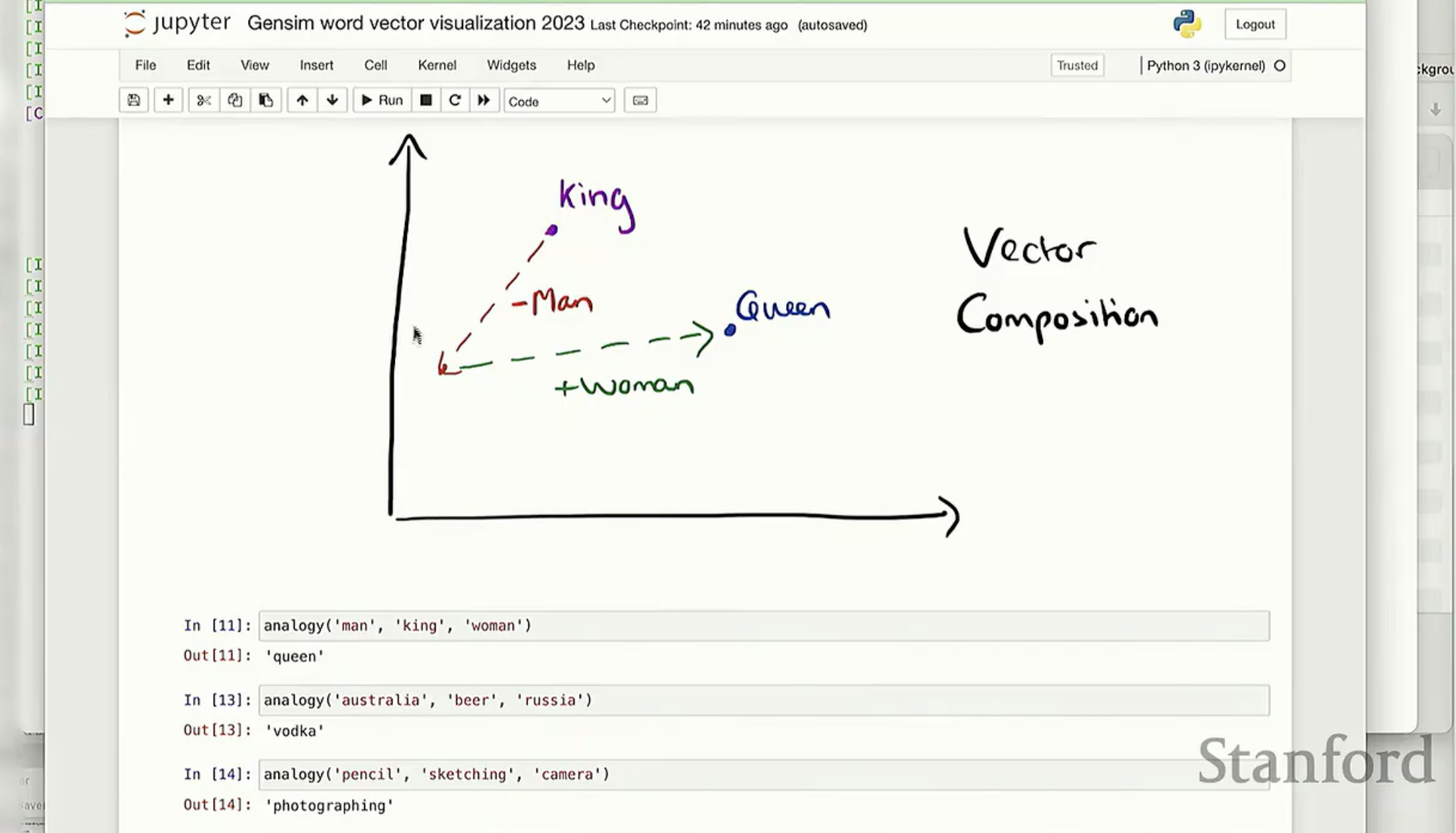
如图 1 所示,通过简单的向量加减法,计算机竟然能够捕捉到“性别”或者“地理位置”这种高级语义维度。例如:
Vector(King) - Vector(Man) + Vector(Woman) = Vector(Queen)
Vector(Australia) - Vector(Beer) + Vector(Russia) = Vector(Vodka)
这种通过向量方向和距离来表达语义的方式,正是我们接下来要拆解的 Word2vec 算法的核心魔力。
1.3 Word2vec 的基本思想
Word2vec 并不是一个单一的模型,而是一系列算法的组合。其核心逻辑在于:
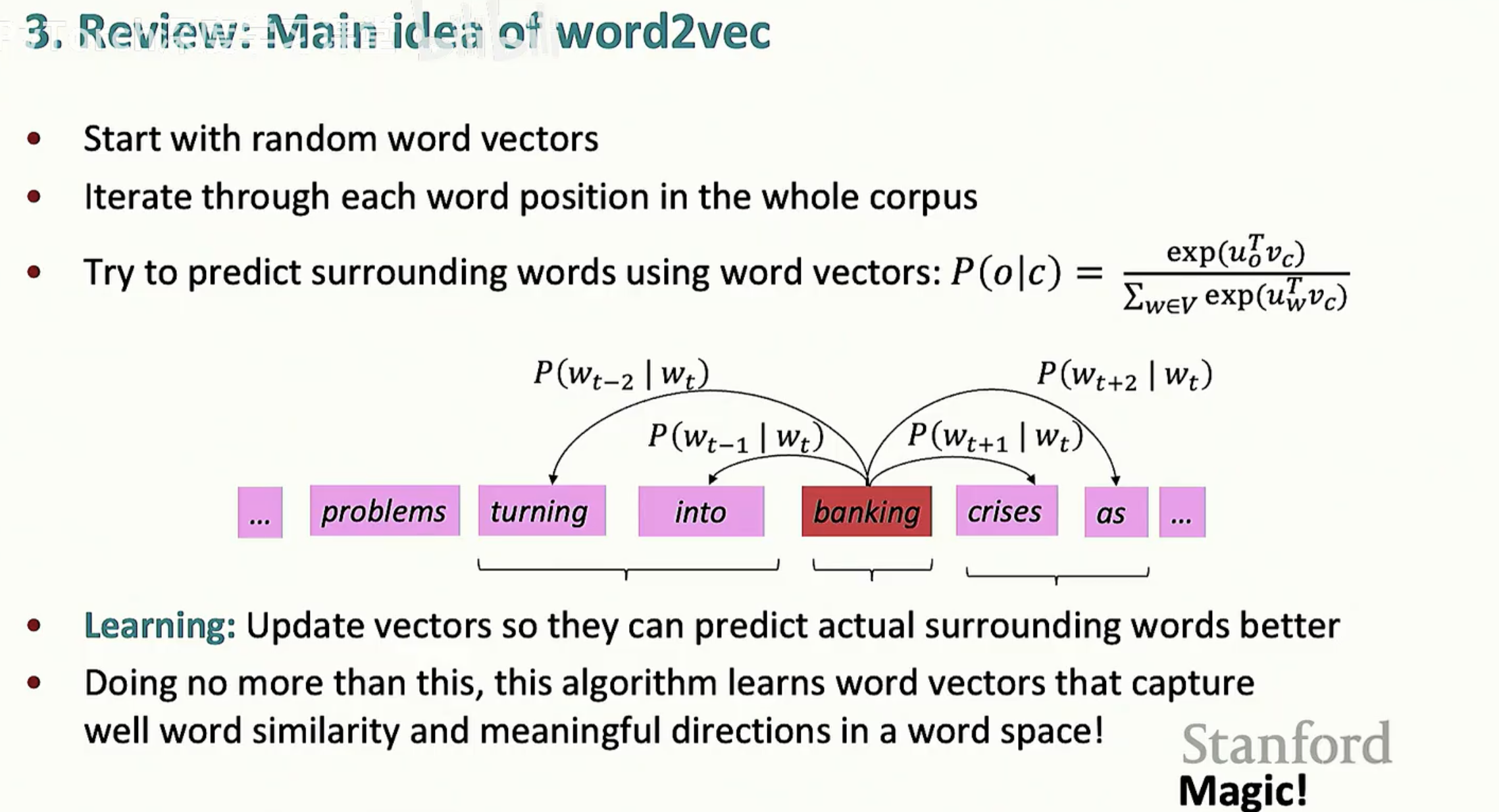
随机初始化:为每个词分配一个随机的向量。
迭代语料库:遍历整个文本流中的每一个位置。
预测上下文:利用当前词的向量来预测它周围可能出现的词。
学习与更新:如果预测不准,就通过优化算法调整向量,使得预测结果越来越接近真实情况。
第二节:词向量从条件概率到目标函数
Word2vec 的核心是一个极简的预测任务:给定一段文本,我们利用中心词(Center word)去预测它周围出现的词(Outside words)。这个模型被称为 Skip-gram。

2.1 概率模型:Softmax 的应用
假设我们有一个中心词 c 和一个它周围的词 o。我们的目标是计算在一个给定的中心词条件下,某个特定词作为其外部词出现的概率 P(o|c)。
为了实现这一点,我们为每个词 $w$ 维护两个向量:
v_w:当 w 是中心词时的向量。
u_w:当 w 是外部词时的向量。
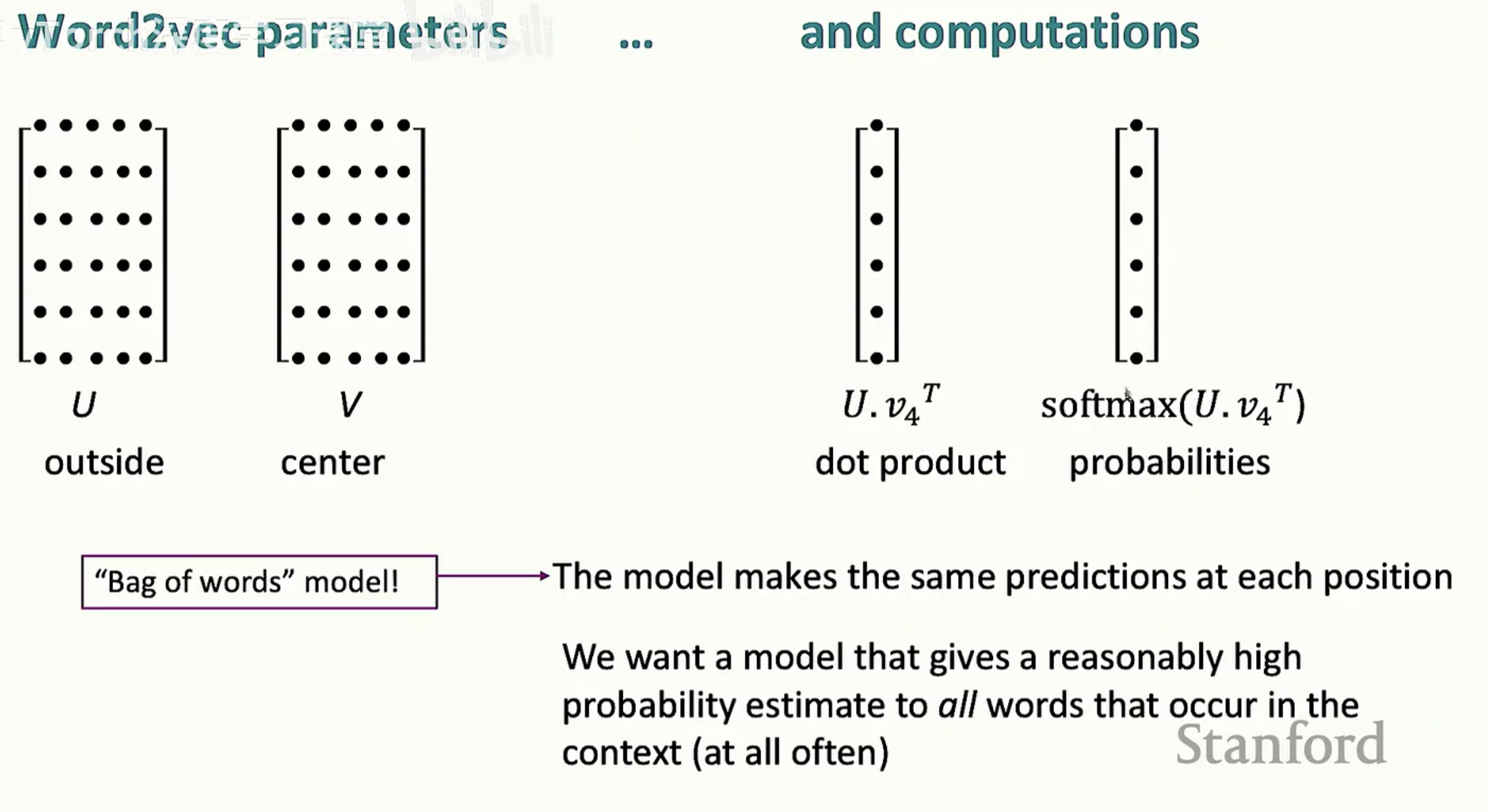
计算公式如下:
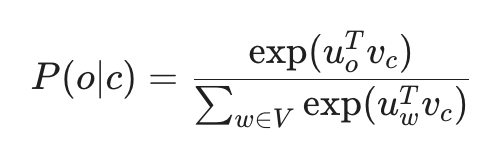
这里的逻辑非常直观:
点积(Dot Product) u_o^T v_c 衡量了两个向量的相似度。点积越大,概率越高。
指数函数 exp 确保所有结果为正数。
分母的求和 则是为了归一化,使得整个词表的所有词概率之和为 1(这就是标准的 Softmax 函数)。
2.2 目标函数:我们要最小化什么?
在训练过程中,我们希望模型对实际出现的词预测概率越高越好。数学上,我们通过最小化负对数似然(Negative Log Likelihood)来实现:
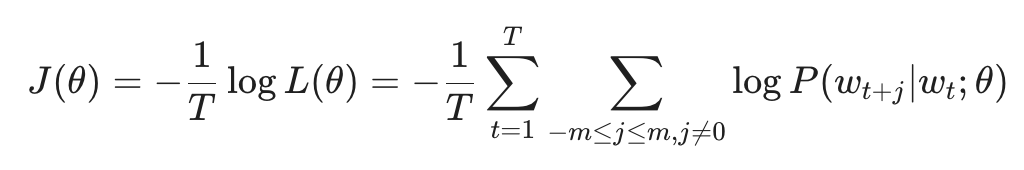

这个 J(theta) 就是我们的代价函数(Cost Function)。模型的目标非常简单:通过不断调整向量 u 和 v,让这个代价函数降到最低。
2.3 训练的挑战:Softmax 太慢了
虽然上面的公式在数学上很完美,但在工程实现上却有一个巨大的坑。

注意看分母。如果我们的词表有 100 万个词,模型每一步更新都要计算 100 万次点积。这在计算上极其昂贵,也是为什么我们需要在后续章节中引入“负采样(Negative Sampling)”的原因。
第三节:模型优化
为了最小化我们在上一节定义的代价函数 J(theta),我们需要一种系统的方法来更新模型参数(即所有的词向量)。在深度学习中,最常用的工具就是梯度下降。
3.1 梯度下降
梯度下降的直觉非常简单:将代价函数想象成一个山谷,我们的目标是找到山谷的最低点。
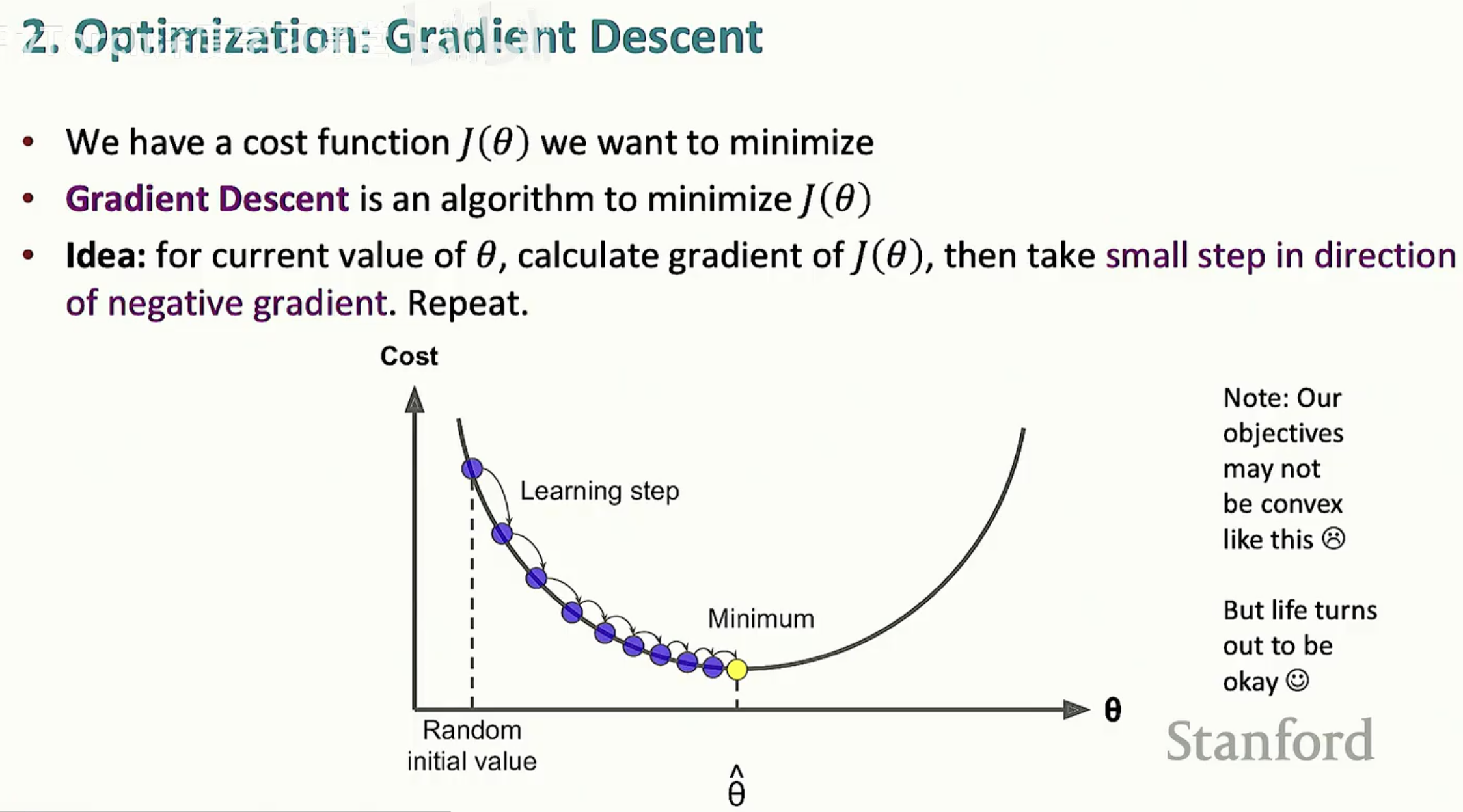
在数学上,我们通过计算代价函数对参数 theta 的梯度来确定“下山”的方向。更新公式如下:
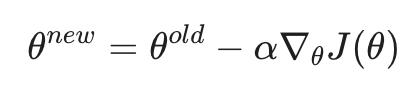
其中 alpha 被称为学习率(Learning Rate)或步长,它决定了我们每一步迈出的距离。如果 alpha 太大,我们可能会越过最低点;如果太小,收敛速度会慢得令人绝望。
3.2 现实的难题:全量梯度下降的瓶颈
虽然上述算法在理论上可行,但在处理 NLP 任务时会遇到一个巨大的问题。我们的代价函数 J(theta) 是语料库中所有窗口的函数。

如果你的语料库有数亿个单词,那么在更新一次词向量之前,你需要遍历整个语料库来计算梯度。这在工程上是不可接受的。
3.3 解决方案:随机梯度下降 (SGD)
为了解决计算速度问题,我们引入了随机梯度下降 (Stochastic Gradient Descent, SGD)。
核心思想:不再等待遍历完整个语料库,而是每看到一个窗口(或一小批窗口 Mini-batch),就立即计算梯度并更新一次词向量。
算法逻辑:
随机采样一个窗口(window)。
计算该窗口下的梯度。
立即更新参数 theta。
回到第一步重复执行。
通过这种方式,我们可以在极短的时间内进行成千上万次的参数微调。尽管单次更新的方向可能由于随机性而略有偏差,但从宏观上看,它依然能高效地带领模型走向“山谷”的最低点。
第四节:负采样 (Negative Sampling)
在标准的 Word2vec 模型中,每一步更新都需要对整个词表的概率进行归一化,这在工程上几乎不可行。Mikolov 等人在 2013 年提出的 负采样(Negative Sampling) 方案,将一个复杂的“多分类”问题转化为了简单的“二分类”问题。
4.1 核心逻辑:从“预测”到“辨析”
负采样的思路非常巧妙:
正样本:给定一个中心词,尝试最大化其周围真实出现的外部词(Real outside word)的概率。
负样本:随机抽取 K 个词作为“噪声词”(Random words),并尝试最小化这些词在当前中心词周围出现的概率。
这意味着,模型不再问“下一个词是 100 万个词中的哪一个?”,而是问“这个词是真实存在的,还是我随机抽取的噪声?”。
4.2 数学实现:Sigmoid 函数的引入
为了处理这个二分类问题,我们放弃了昂贵的 Softmax,改用 Sigmoid 函数。

如图 8 所示,我们的目标函数变为最小化两个对数概率之和:
左项:最大化真实观测到的对(Center-Outside)的概率。
右项:最大化那些“噪声词”不出现的概率。
4.3 采样策略:为什么是 3/4 次方?
我们应该如何抽取那些负样本(噪声词)呢?如果完全随机,频率极高的词(如 "the", "a")会一直被抽到。为了平衡,Word2vec 使用了一个经过微调的概率分布:
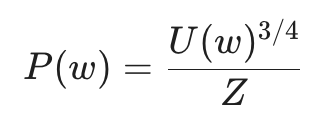
这里的 3/4 次方 是一个经验值。它能稍微增加低频词被抽中的频率,确保模型不会只盯着那些常见的虚词,而是能够更全面地学习整个词表的语义空间。
第五节:共现矩阵与 GloVe
除了 Word2vec 这种每次只看一个局部窗口的迭代方法,NLP 领域还有一类长久存在的方法:基于共现矩阵(Co-occurrence Matrix)。
5.1 传统的共现向量 (Co-occurrence Vectors)
最直接的想法是:如果两个词经常出现在一起,它们就应该有相似的含义。我们可以构建一个巨大的矩阵,记录每个词在语料库中与其他词共同出现的次数。

这种方法虽然利用了全局统计信息(即看到了整个语料库的全貌),但它面临着严重的工程挑战:
维度灾难:词表有多大,向量就有多长。
高维稀疏:存储开销巨大且包含大量噪声。
解决方法:通常使用奇异值分解(SVD)将这些高维向量压缩到较低的维度(如 25-1000 维),从而提取出稠密的语义特征。
5.2 桥接两大流派:GloVe 模型
Word2vec 擅长捕捉复杂的语义模式(如类比推理),但它忽略了语料库的全局统计规律;而 SVD 捕捉了全局信息,但在捕捉语义关联上表现稍逊。
GloVe (Global Vectors) 应运而生,它的目标是将这两者的优点结合起来。

GloVe 的核心洞察在于:共现概率的比率(Ratio)比单纯的概率更能体现词与词之间的微妙关系。
5.3 为什么 GloVe 更高效?
GloVe 的目标函数本质上是在做一种特殊的“带权重的最小二乘回归”:
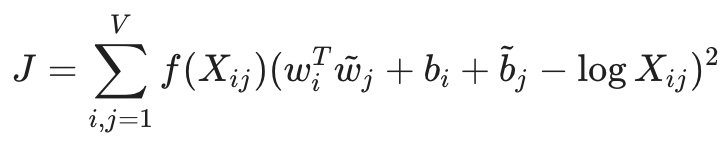
它直接拟合词与词共现次数的对数值。
它使用权重函数 f(Xij) 来平衡:既不让高频词(如 "the")主导损失函数,也不让罕见词产生过多噪声。
最终结果:GloVe 既拥有 Word2vec 那种神奇的线性类比能力(King - Man + Woman = Queen),又能在训练时更充分地利用语料库的全局信息。
第六节:我们如何衡量词向量的好坏?
即便模型在数学上收敛了,我们依然需要评估生成的词向量在实际应用中的质量。在 NLP 领域,评估通常分为两个维度:内部评估与外部评估。
6.1 内部评估 (Intrinsic Evaluation)
内部评估侧重于考察词向量在特定语义任务(如类比或相关性)上的表现。
词比喻任务 (Word Vector Analogies):
这是最著名的评估方法。我们考察向量空间是否满足 a:b :: c:d 的关系。

语义相关度评分:
将词向量计算出的余弦相似度与人类专家的主观评分(如 WordSim353 数据集)进行对比。如果两者的相关性越高,说明模型越符合人类的直觉。
6.2 外部评估 (Extrinsic Evaluation)
外部评估则是将词向量作为预训练特征,投入到具体的下游 NLP 任务中,例如:
命名实体识别 (NER):识别文本中的人名、地名。
情感分析 (Sentiment Analysis):判断评论的正负面倾向。
如果换上这套词向量后,下游任务的准确率提升了,那么这套词向量就是成功的。
6.3 词向量的局限性
尽管 Word2vec 和 GloVe 极大地推动了 NLP 的发展,但它们也存在明显的局限:
一词多义 (Polysemy):在静态词向量中,“Bank”无论是代表“银行”还是“河岸”,都共享同一个向量。
词序缺失:由于基于窗口或共现,模型往往忽略了句子中长距离的逻辑依赖。

