一、密度估计

图中说明了对多维特征向量进行密度估计的设定与公式。

• 训练集：{x⁽¹⁾,x⁽²⁾,…,x^(m)}，每个样本 x_i 有 n 个特征。右侧用列向量表示样本 xx由各维特征组成（x₁,x₂,…,x_n）；右上角坐标轴用 x₁（横轴）与 x₂（纵轴）示意二维情形。

• 模型假设与密度分解：红色公式给出整体密度对各维的分解

  

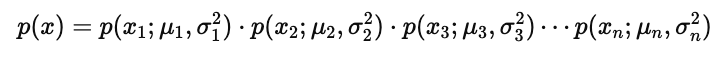
  等价写为

  

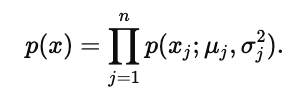
  蓝色箭头标注每一维都有自己的均值 μ_j 与方差 σ_j²（一维分布）。

• 概率示例（右下角）：给出两维事件的概率并用独立性相乘：

  

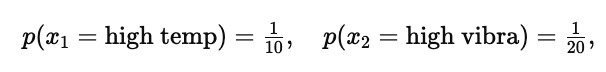
  因而

  

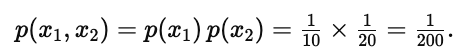
• 记号说明（左下角）：∑→+，∏→×，把求和符号理解为加号、连乘符号理解为乘号。

二、异常检测算法步骤

图中展示了基于高斯分布的异常检测算法流程。

1. 选择特征
   从数据中挑选 nn 个可能与异常有关的特征 x_i。

2. 估计参数
   对每个特征 x_j：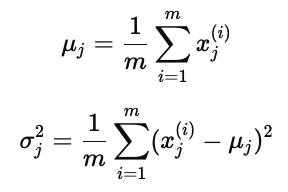

   

   图中红色曲线示意了数据点分布以及概率密度函数 p(x_j)。

3. 计算概率并判定异常
   对新样本 x，计算联合概率：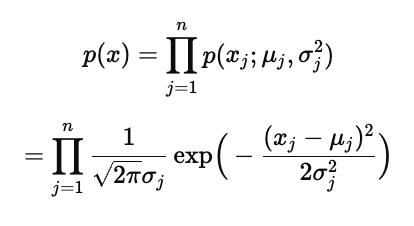

   

   如果

   

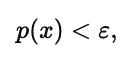
   则判定该样本为异常。

异常检测示例

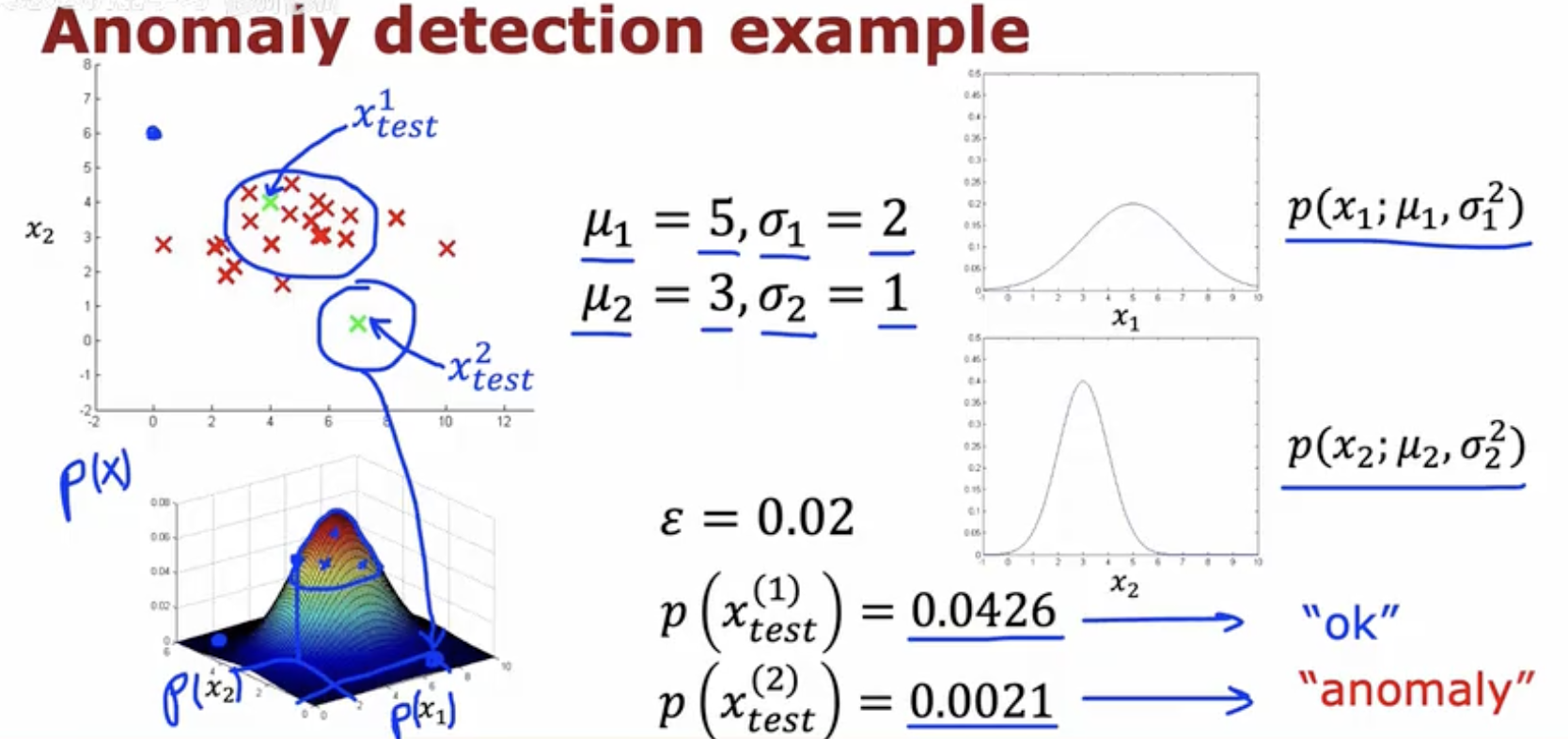
图中展示了利用高斯分布模型进行异常检测的具体例子。

• 参数设定：

  μ₁=5, σ₁=2, μ₂=3, σ₂=1

• 分布可视化：右侧分别展示了特征 x₁、x₂​ 的高斯分布曲线 p(x₁;μ₁,σ₁²)、p(x₂;μ₂,σ₂²)。左下角三维图给出了联合分布 p(x)。

• 判别阈值：设定 ε=0.02。

• 测试样本结果：

  

左上角的散点图直观展示了：第一个测试点位于正常数据分布区域内，而第二个测试点远离主要分布区域，因此被判定为异常。

三、总结

异常检测算法的核心思想是通过学习数据的正常分布来识别偏离该分布的点。算法一般分为以下几个关键步骤：

1. 特征选择：挑选能够反映数据正常与异常差异的特征。

2. 参数估计：利用训练数据估计特征的分布参数（如均值和方差）。

3. 概率计算：在新样本到来时，根据分布模型计算其出现的概率。

4. 阈值判断：设定阈值 εε，若样本概率低于该值，则判定为异常。

总体来说，异常检测算法依赖于概率建模与统计判断，能够有效识别与正常模式差距较大的数据点。