一、正态分布的定义

正态分布（Normal Distribution），又称高斯分布（Gaussian Distribution），是统计学和概率论中最经典、最重要的一种分布形式。它的曲线形状呈对称的钟形，中间高、两边低，且以均值为中心对称展开，数据大多集中在均值附近，越往两端越稀少。正态分布由均值和方差两个参数决定：均值决定曲线的中心位置，方差决定曲线的宽窄程度。由于许多自然现象和社会现象都符合或近似符合正态分布，例如人的身高、考试成绩、测量误差等，因此它在数据分析和科学研究中具有极其重要的地位。

通俗理解：

正态分布可以理解为“多数集中在中间，两边逐渐减少”，就像大部分人身高差不多，而特别矮或特别高的人数就比较少。

二、正态分布的公式与形状对照图

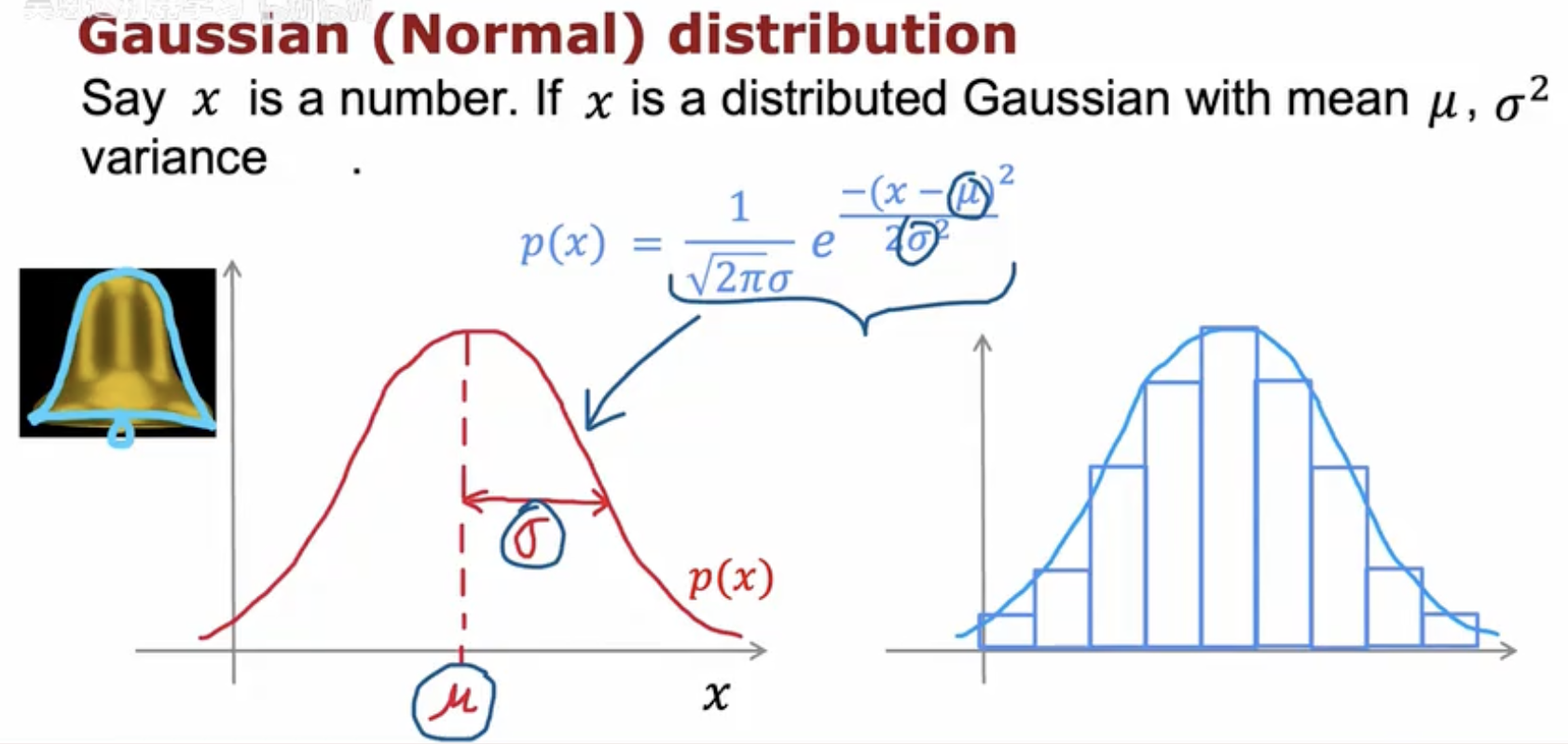
设 x 为一个数，若 x 服从均值为 μ、方差为 σ² 的高斯（正态）分布。

公式给出正态分布的概率密度函数：

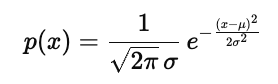
中间的红色钟形曲线表示 p(x) 随 x 的变化；横轴为 x，曲线旁标注 p(x)。虚线竖线落在曲线中心并在横轴处标记 μ，表示均值位置；从中心向右的水平短线标记 σ，示意标准差对应的横向尺度。

左下角的小金色“铃铛”图标用来比喻该曲线的“钟形”外观，与红色曲线的形状相呼应。

右侧蓝色直方图展示样本频率分布，外层叠加的平滑蓝色曲线与之对照，表示理论上的正态密度与样本直方图的大致贴合关系。

三、不同均值与标准差下的高斯分布对比

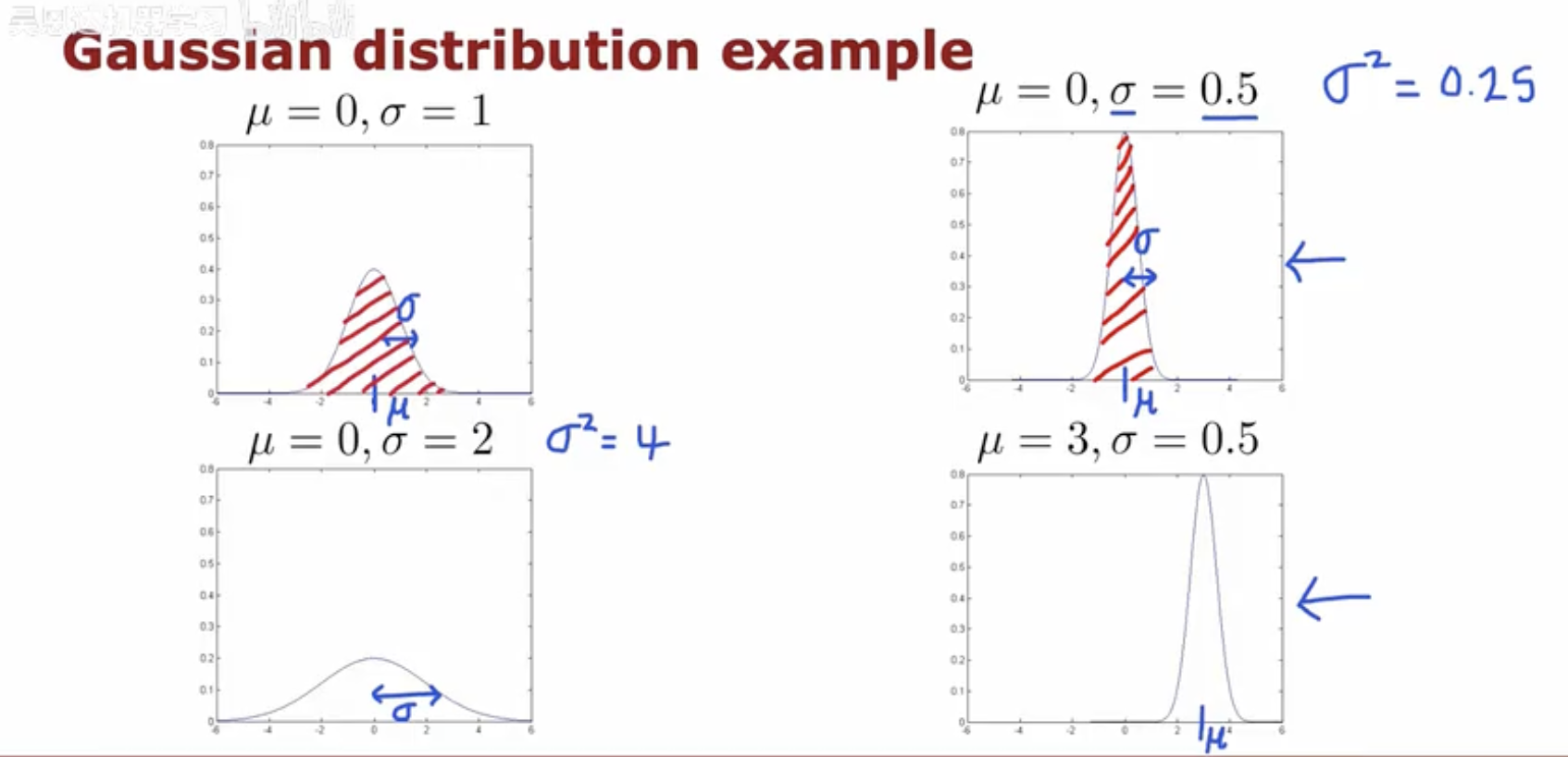
整张图对比参数变化对曲线形状与位置的影响。横轴为数值 x，纵轴为密度，刻度最高到约 0.8。蓝色手写标注处给出方差数值（如 σ2=0.25、σ2=4）并用箭头指向对应子图。

左上角：标注 μ=0, σ=1。曲线是对称的钟形，底部中央用 “μ” 标出中心位置，曲线内部用红色斜线区域着色，并用左右双向蓝箭头标出 σ 的横向尺度，表示此时的“宽度”基准。

右上角：标注 μ=0, σ=0.5，旁边手写 σ2=0.25 并有箭头指向该图。曲线比左上更瘦更高，红色斜线着色区域明显变窄，蓝色双向箭头所示的 σσ 水平距离变短，底部同样以 “μμ” 标记中心在 0。

左下角：标注 μ=0, σ=2，旁边手写 σ2=4。曲线比左上更扁更宽，蓝色双向箭头所示的 σ 横向跨度变大，中心仍在 0，并在底部以 “μ” 标记。

右下角：标注 μ=3, σ=0.5。曲线形状与右上角相似（瘦高），但整体向右平移到 x=3 附近；底部在 3 的位置用 “μ” 标记中心。右侧蓝色箭头标注用于强调这是被平移后的那一幅。

四、正态分布参数估计

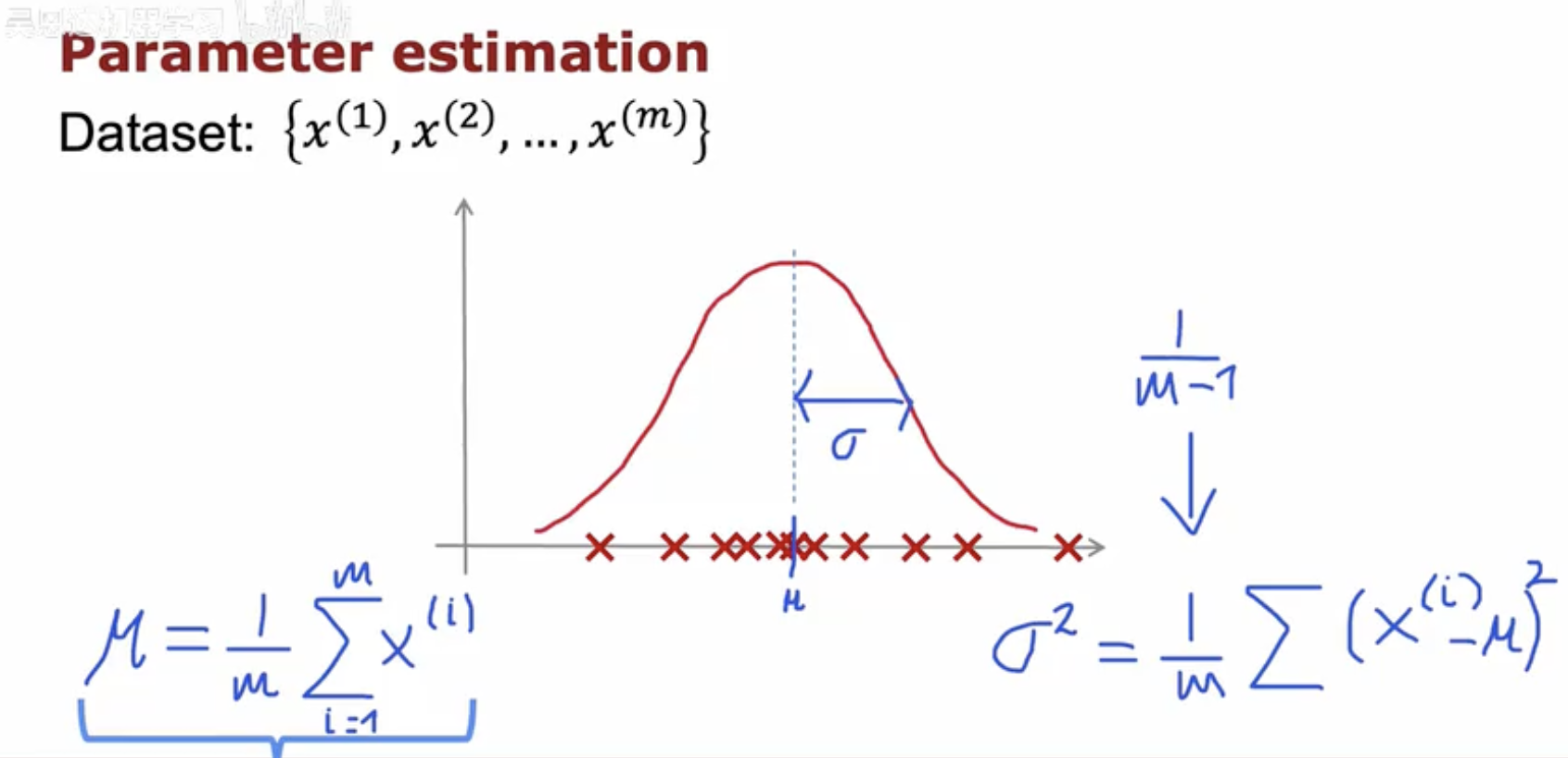
图展示如何从数据集中估计正态分布的参数。左上角给出数据集形式 {x⁽¹⁾,x⁽²⁾,...,x^(m)}。

图中央是一条红色钟形曲线，横轴上标有多个红色叉号，表示采样到的数据点。虚线竖线标记均值 μ 的位置，曲线上用水平箭头标注 σ，表示标准差对应的范围。

左下角写有均值的估计公式：

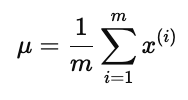
右下角写有方差的估计公式：

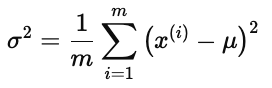
右上角还标注了 1/(m−1​) 的形式，提示在样本量有限时会使用无偏估计公式。整幅图通过公式与曲线直观展示了如何用样本点来计算正态分布的参数均值 μ 和方差 σ²。