一、信息增益的定义

信息增益（Information Gain）是机器学习中，特别是在构建决策树时，用来评估某个特征对分类结果贡献大小的一个指标。它基于信息论中的熵（Entropy）概念，熵是衡量数据集纯度或不确定性的量度。信息增益通过计算数据集在某个特征上的熵的减少量来确定该特征的价值。

通俗理解：

如果我们有一个混乱的数据集，信息增益帮助我们找到一个特征，这个特征能够最好地将数据集划分为更有序、更纯的小组。信息增益越大，意味着使用这个特征进行分裂可以显著提高数据的有序性，减少混乱。在决策树中，我们通常选择信息增益最大的特征作为节点分裂的依据，因为这样的分裂可以最大程度地提高分类的准确性。

信息增益的计算涉及到原始数据集的熵和分裂后子集的熵的加权平均。这个过程实际上是在寻找能够最大化分类信息的分裂点，从而帮助模型更有效地学习和预测。简而言之，信息增益是决策树学习算法中用于优化决策路径的关键工具。

二、信息增益计算示例

1. 初始状态：

   • 根节点（root）中猫的比例 p₁^root​=5/10=0.5。

2. 分裂属性：

   • 选择“耳形（Ear shape）”作为分裂属性，分为“尖耳（Pointy）”和“垂耳（Floppy）”两个子节点。

3. 子节点状态：

   • 尖耳子节点中，猫的比例 p₁^left​=4/5，权重 w^left=5/10。

   • 垂耳子节点中，猫的比例 p₁^right​=1/5，权重 w^right=5/10。

4. 信息增益公式：

   • 信息增益计算公式为：

   • 其中，H(p_1​) 表示熵，w 表示权重（子节点中样本数占总样本数的比例）。

这幅图通过一个具体的例子展示了如何计算信息增益，以选择最佳的分裂属性。

三、决策树学习的基本步骤

1. 开始：从根节点开始，包含所有样本。

2. 计算信息增益：对所有可能的特征计算信息增益，并选择信息增益最高的特征。

3. 分裂数据集：根据选定的特征分裂数据集，创建树的左分支和右分支。

4. 重复分裂过程：继续重复分裂过程，直到满足停止条件：

   • 节点是100%的一个类别。

   • 分裂节点会导致树超过最大深度。

   • 额外分裂的信息增益小于设定的阈值。

   • 节点中的样本数低于设定的阈值。

四、决策树的递归分裂过程

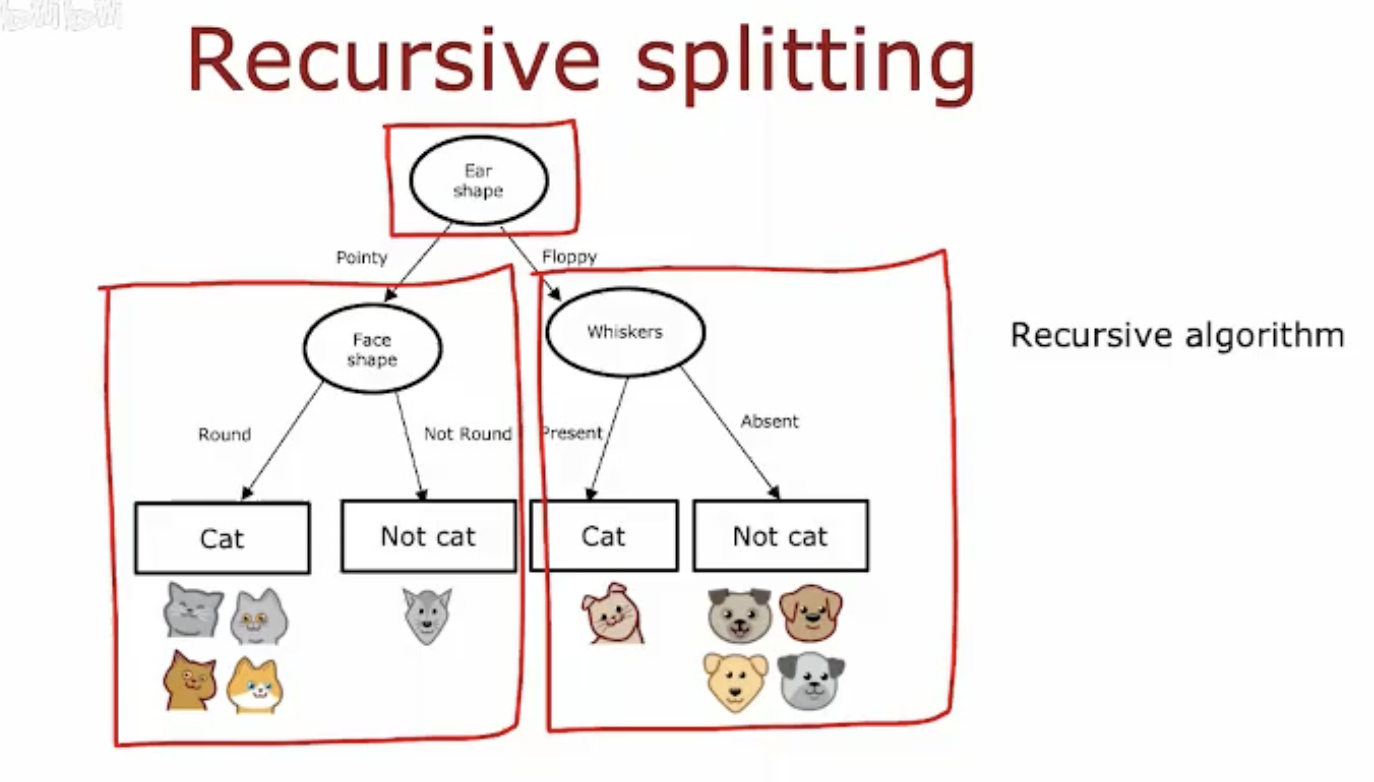
这幅图展示了决策树中的递归分裂过程：

1. 根节点：从“耳形”（Ear shape）特征开始分裂。

2. 第一次分裂：

   • 如果耳形是“尖耳”（Pointy），则根据“脸型”（Face shape）进一步分裂。

     • 如果脸型是“圆脸”（Round），则分类为“猫”（Cat）。

     • 如果脸型不是圆脸，则分类为“非猫”（Not cat）。

   • 如果耳形是“垂耳”（Floppy），则根据“胡须”（Whiskers）进一步分裂。

     • 如果胡须“存在”（Present），则分类为“猫”（Cat）。

     • 如果胡须“不存在”（Absent），则分类为“非猫”（Not cat）。

3. 递归算法：这个过程是递归的，每个节点都可能根据某个特征进一步分裂，直到满足停止条件。