第一节:计算图定义
在深度学习中,软件并不是直接处理一长串复杂的数学公式,而是将神经网络的方程式表示为一张“图”。这种表达方式不仅让复杂的运算变得直观,更是自动求导技术的基础。
1. 什么是计算图?
计算图(Computation Graph)是数学表达式的一种图形化表示。在这种结构中:
源节点(Source nodes):代表输入量(Inputs)。
中间节点(Interior nodes):代表具体的数学运算(Operations)。
边(Edges):负责传递运算的结果。
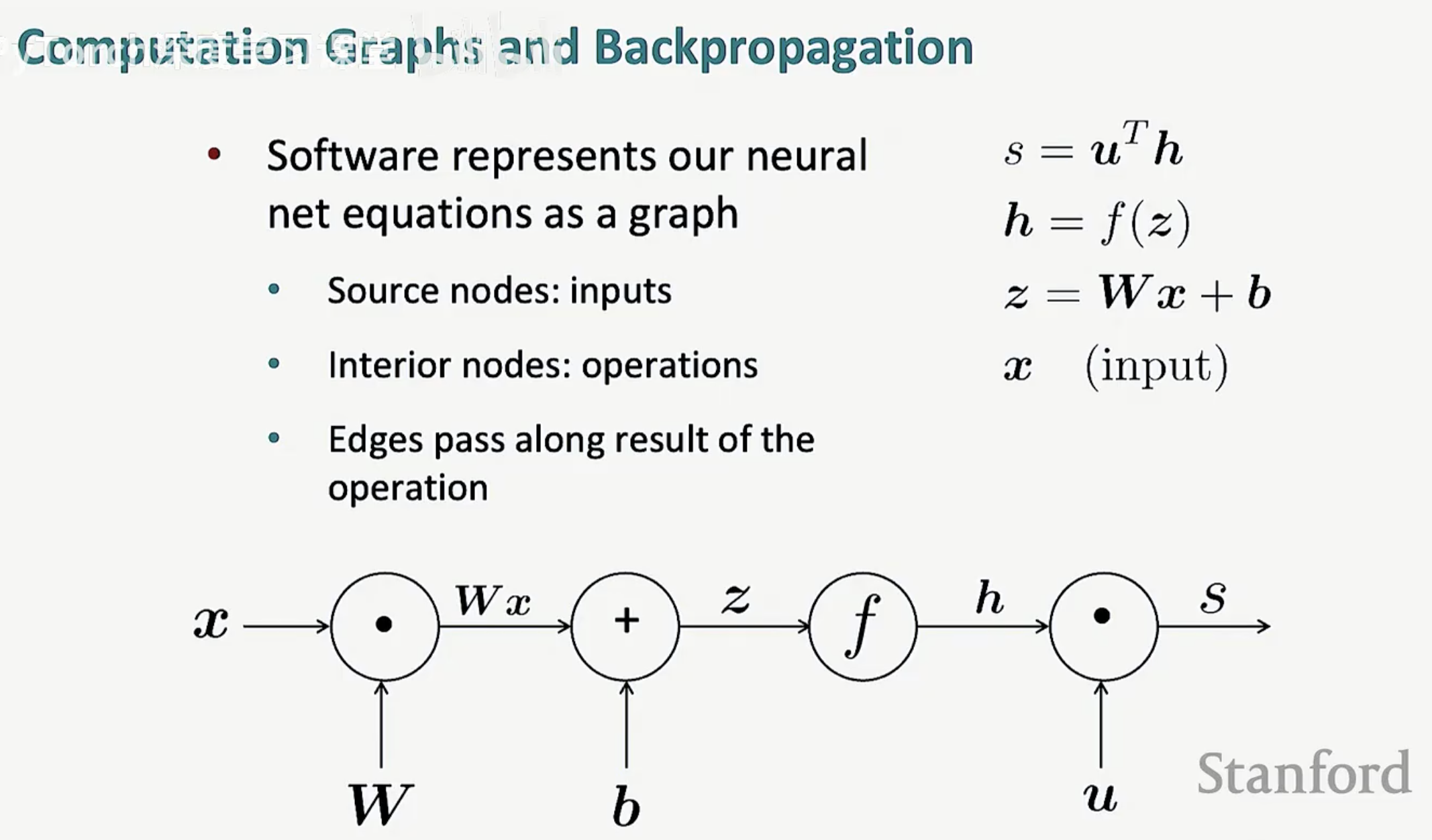
如图所示,方程 z = Wx + b 被拆解为:输入 x 与权重 W 相乘,结果再与偏置 b 相加。每一个圆圈都是一个运算加工厂,而箭头则代表了数据的流动。
2. 反向传播:梯度的“逆流而上”
当我们完成前向计算得到输出 s 后,为了优化模型,我们需要知道每个参数对结果的影响。这时,我们就要沿着边反向运动。
反向遍历:从输出端出发,沿着计算图的边逆向回溯。
传递梯度:在回溯过程中,我们传递的是梯度(Gradients),即输出对某个变量的偏导数。
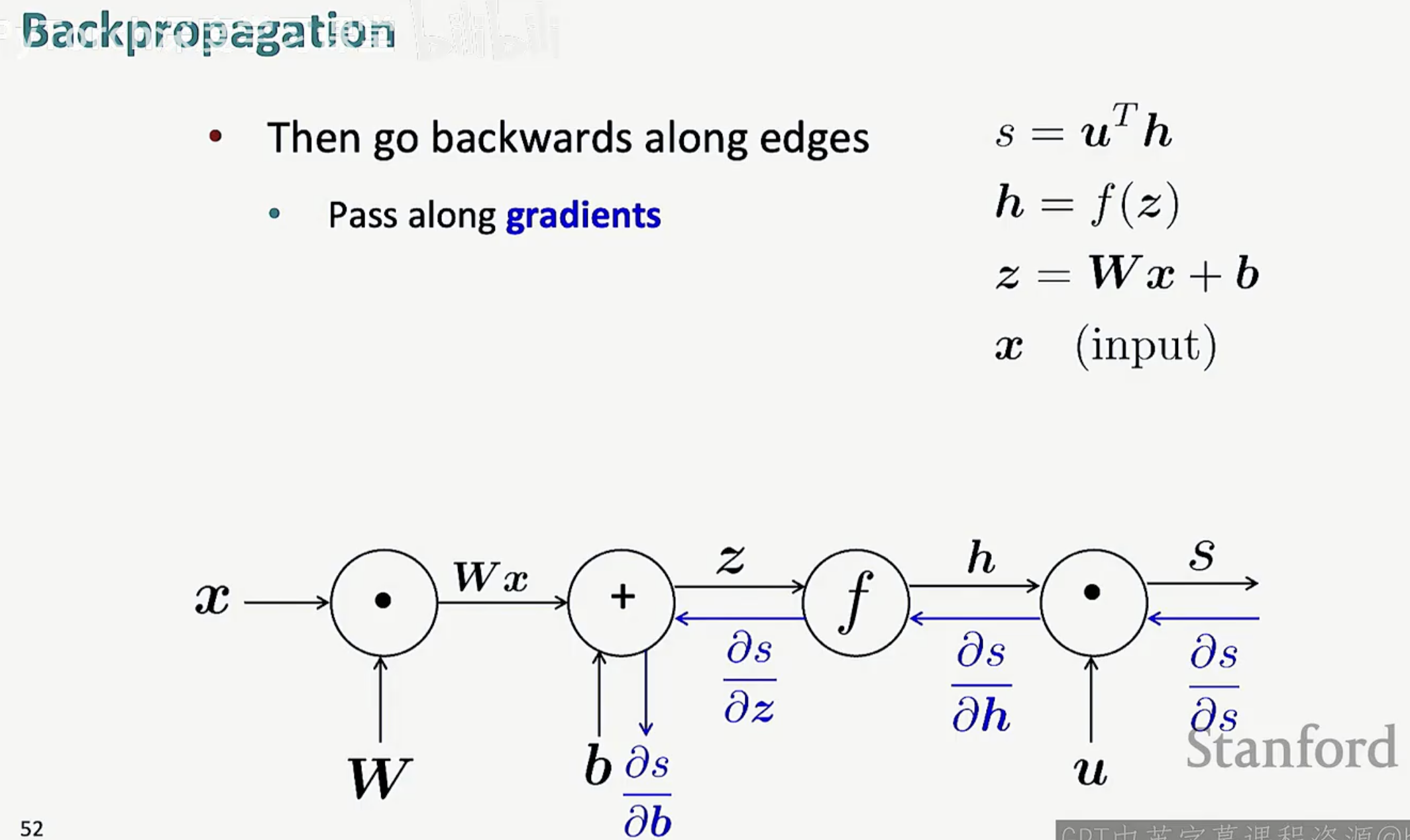
通过这张图可以看到,前向传播(黑色箭头)是在计算“结果”,而反向传播(蓝色箭头)则是在分发“责任”。
3. 单个节点的秘密:局部梯度(Local Gradient)
要实现整个图的反向传播,核心在于理解每一个独立节点是如何处理梯度的。每一个节点其实都自带一种“觉醒”能力:局部梯度。
定义:局部梯度是指该节点的输出相对于其输入的偏导数。
链式法则的协作:
上游梯度(Upstream gradient):从后方传回来的梯度。
下游梯度(Downstream gradient):节点计算出的新梯度,并传给前方。
计算公式:下游梯度 = 上游梯度 x 局部梯度。
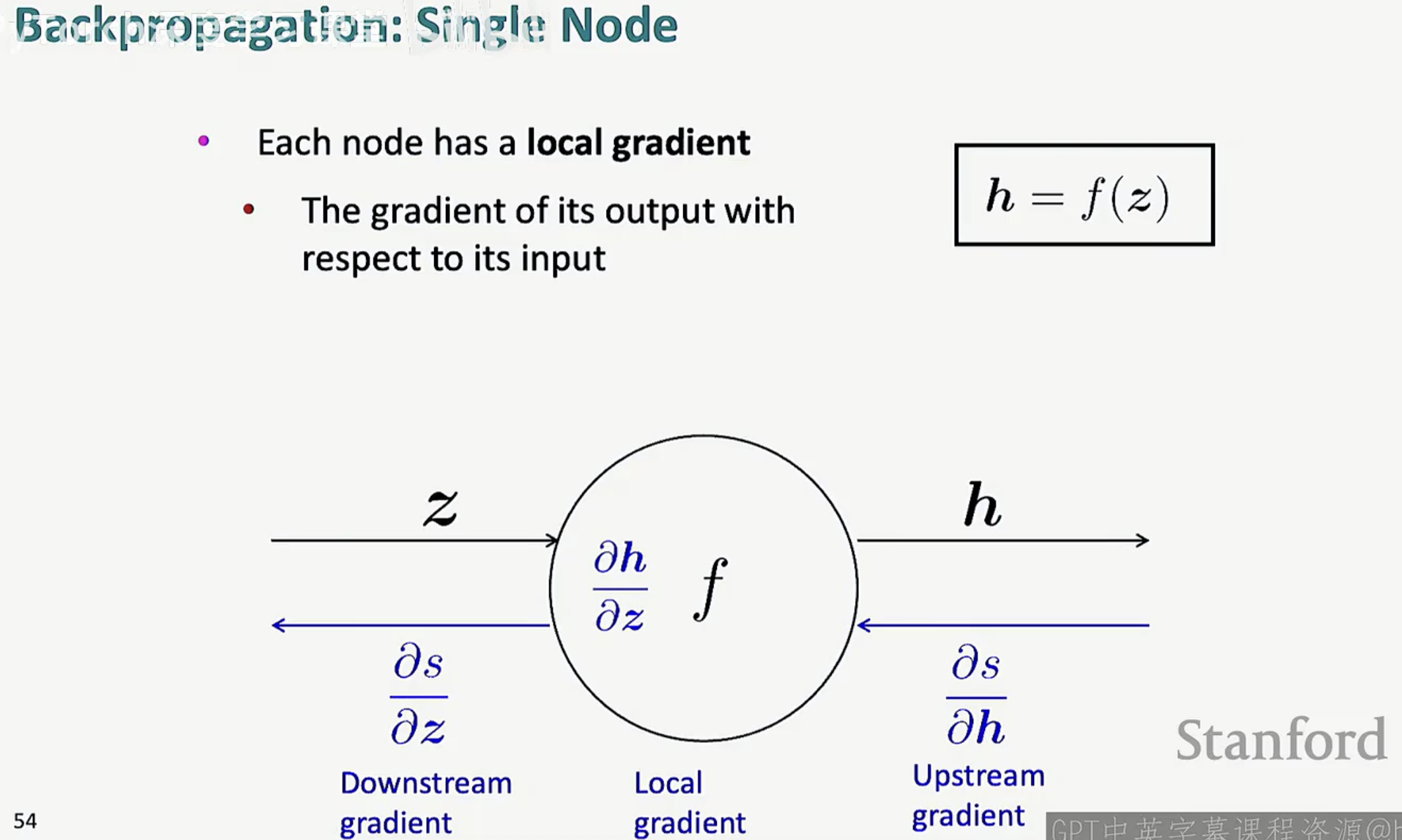
以 h = f(z) 为例,该节点只需要知道自己的局部梯度,然后将其与拿到的上游梯度相乘,就能轻松算出下游梯度 。这种“局部化”的设计,使得无论网络多复杂,每个节点都只需要各司其职。
第二节:多元输入与实战案例推导
1. 多输入节点的梯度分配
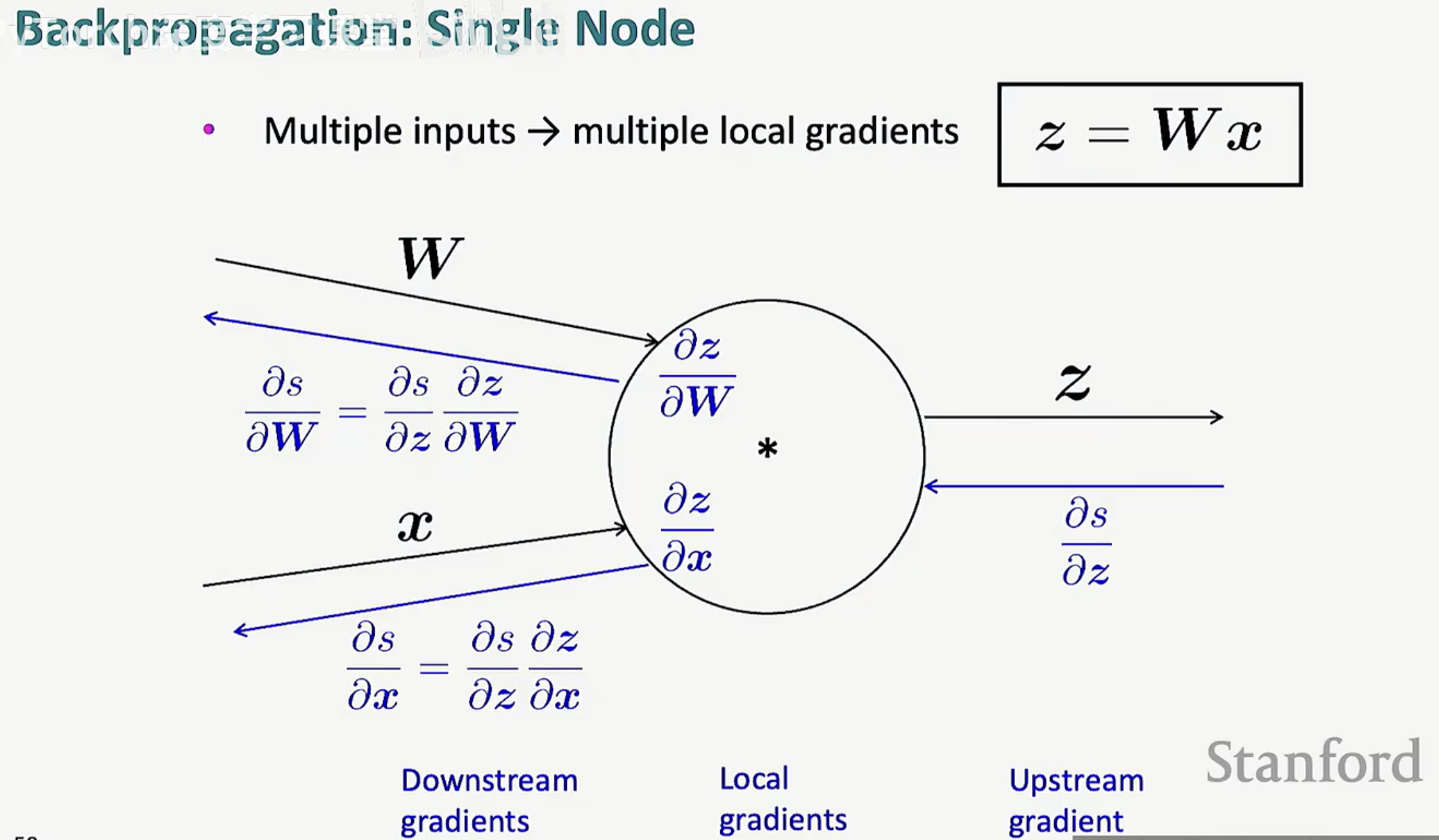
在神经网络中,节点往往不止一个输入。最典型的例子就是矩阵乘法 z = Wx。
多个输入意味着多个局部梯度:当一个操作涉及多个变量时,节点需要分别为每个输入计算局部偏导数。
梯度的分发:同样遵循链式法则。下游梯度等于“上游梯度”乘以“该输入对应的局部梯度”。

2. 全程实战:一个具体的数值例子
为了让抽象的公式落地,我们来看一个包含加法、最大值函数和乘法的综合案例。
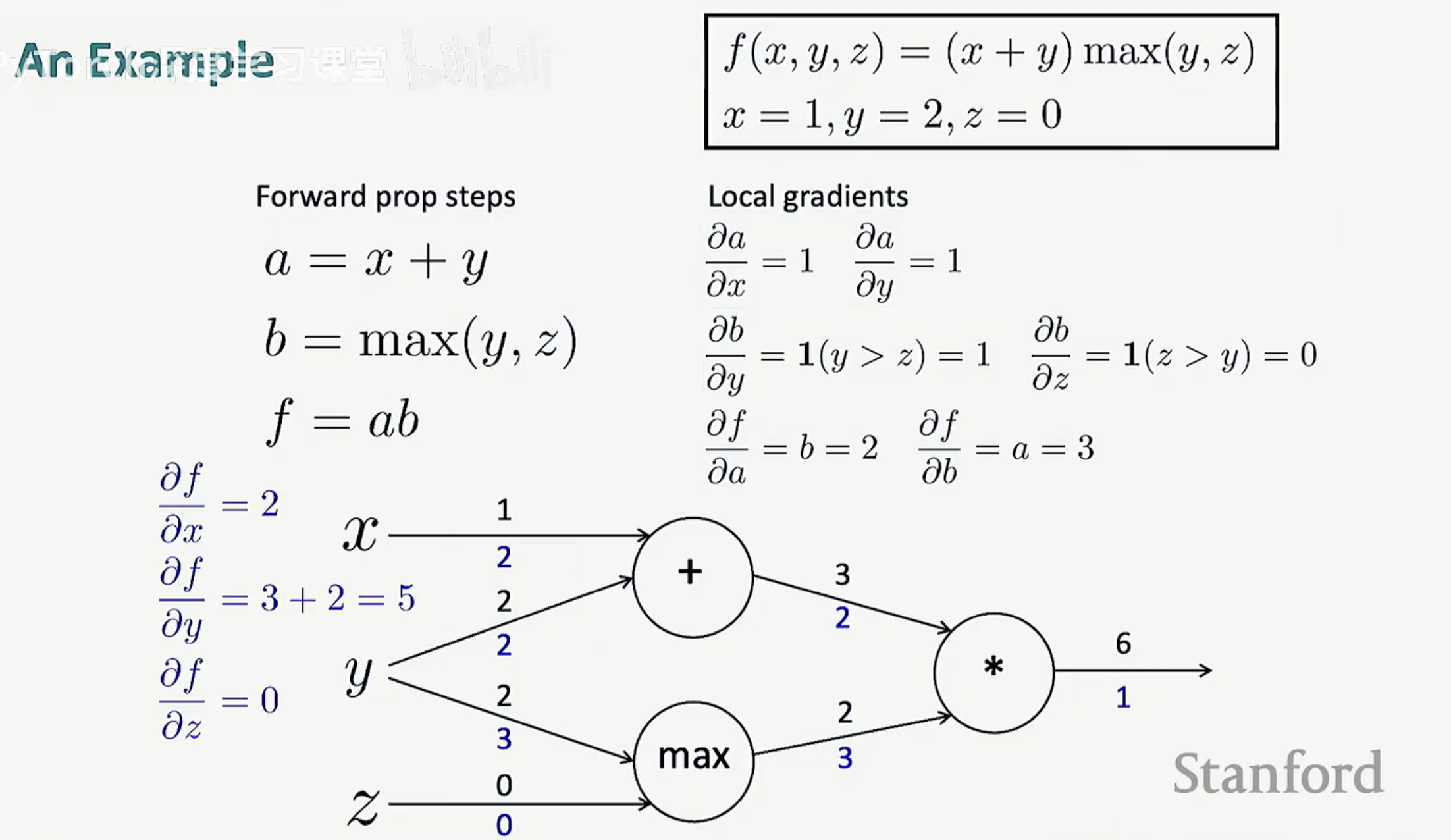
函数表达式为:f(x, y, z) = (x + y) max(y, z)。
设定初始输入为:x = 1, y = 2, z = 0。
第一步:前向传播(计算结果)
我们按照计算图的顺序从左向右计算:
加法节点:a = x + y = 1 + 2 = 3。
Max节点:b = max(y, z) = max(2, 0) = 2。
乘法节点:f = a x b = 3 x 2 = 6。
第二步:计算局部梯度
每个节点根据其数学特性计算偏导数:
乘法节点:对 a 的导数是 b(2),对 b 的导数是 a(3)。
Max节点:因为 y > z,所以对 y 的导数是 1,对 z 的导数是 0。
加法节点:对 x 和 y 的导数均为 1。
第三步:反向传播(计算最终梯度)
从输出端 f 开始,初始梯度为 1,向左回溯:
传给 a:1 x 2 = 2。
传给 b:1 x 3 = 3。
最终输入梯度:

3. 效率的关键:为什么不能独立计算?
在实际的大规模网络中,我们必须通过这种“图遍历”的方式一次性计算所有梯度。
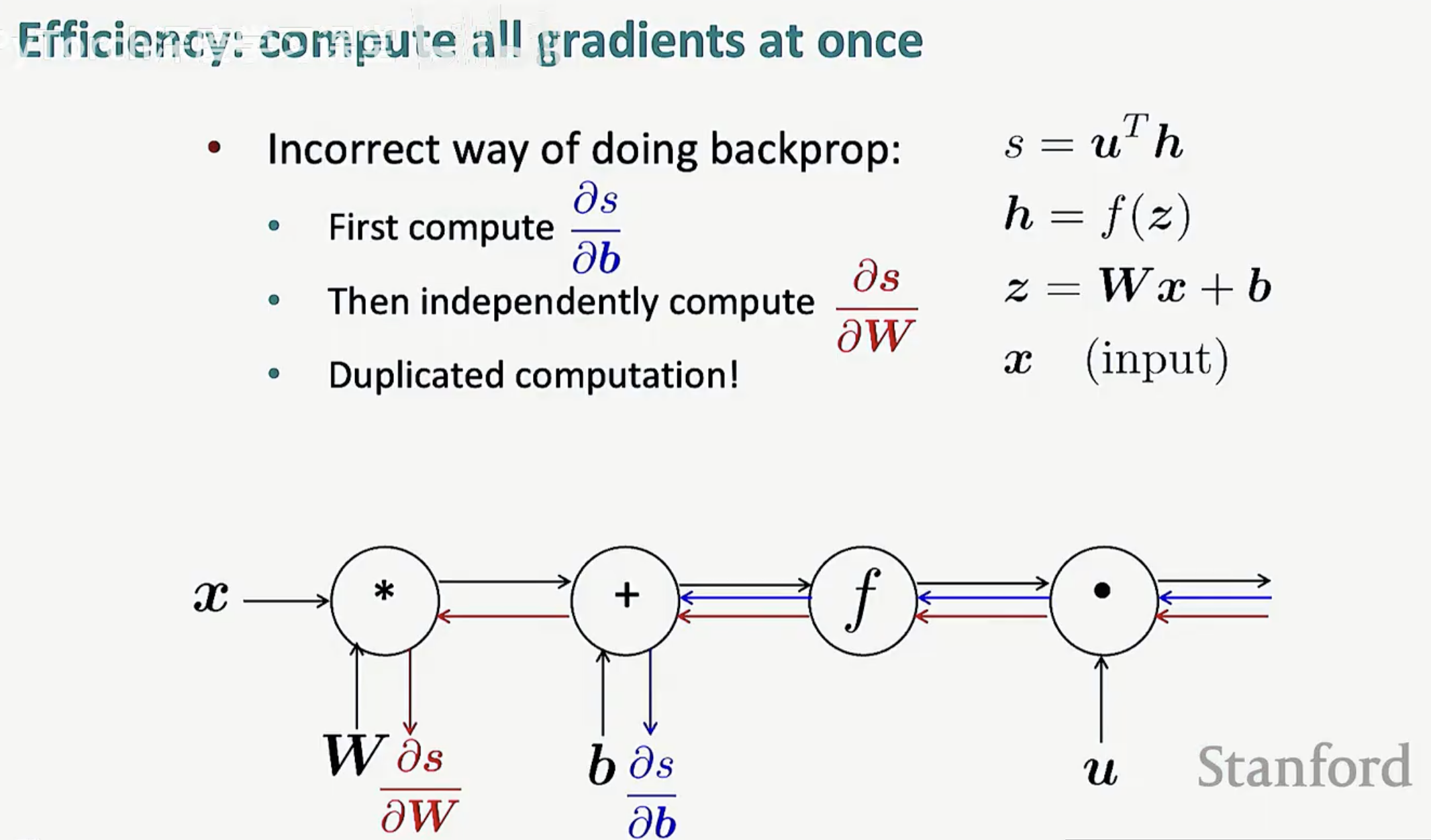
错误做法:如果我们独立地为每个参数(如 W 或 b)单独运行一遍算法,会产生大量的重复计算(Duplicated computation)。
正确做法:先进行一次前向传播,再进行一次统一的反向传播。这种方式的计算复杂度与前向传播处于同一数量级 O(n),极大地提升了效率。
第三节:工程实现——从理论到自动微分框架
1. 通用计算图中的反向传播
在处理任意复杂的神经网络时,我们需要一套标准化的流程来确保梯度计算的正确性与效率:
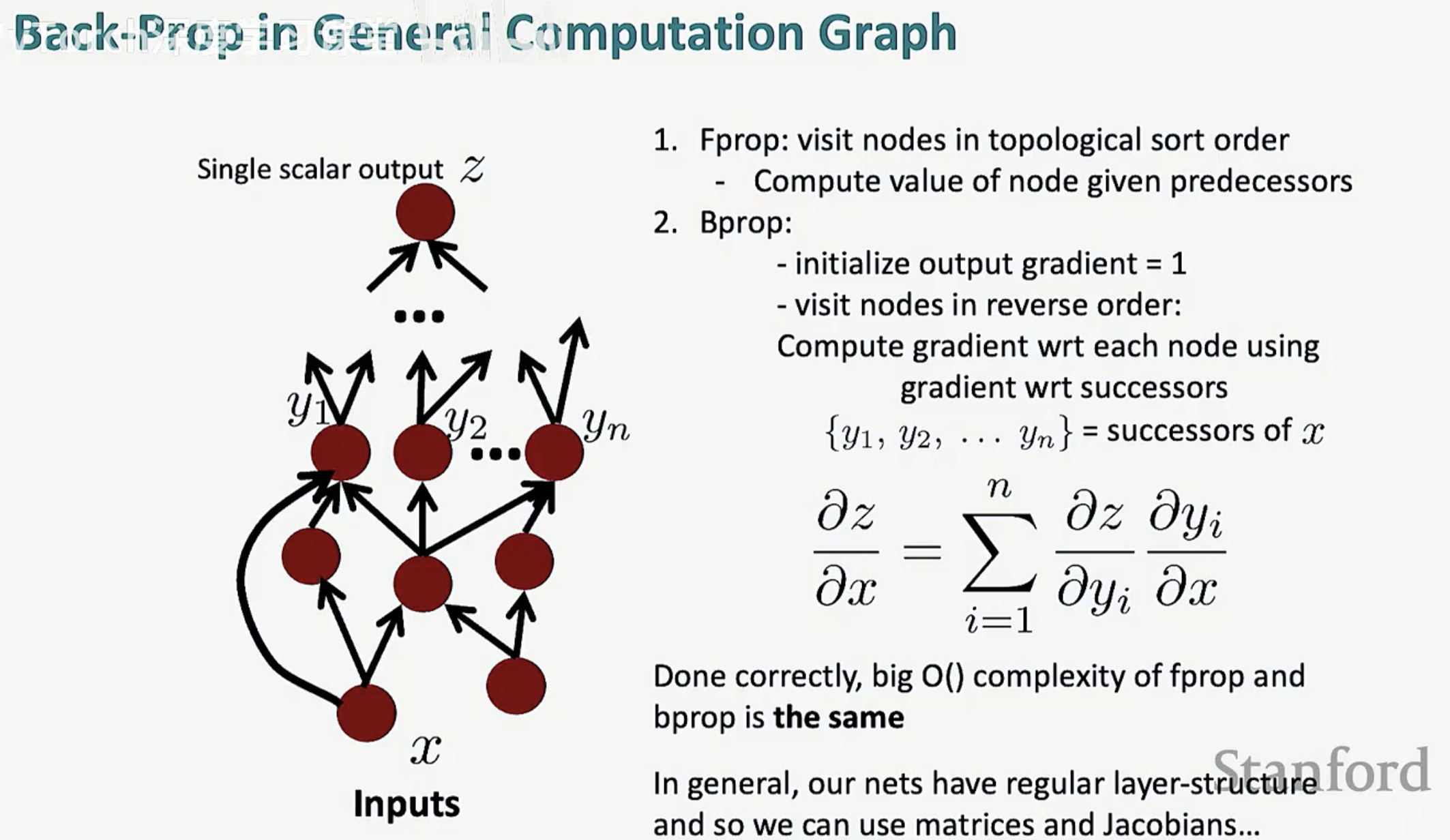
前向传播(Fprop):按照拓扑排序(Topological sort)的顺序访问节点,根据前驱节点的值计算当前节点的值。
反向传播(Bprop):

效率表现:只要实现得当,前向和反向传播的算法复杂度 $O()$ 是完全相同的。
2. 自动微分(Automatic Differentiation)
现代深度学习框架(如 PyTorch 和 TensorFlow)的核心就是自动微分。它极大地减轻了开发者的负担:
符号推导:梯度计算可以从前向传播的符号表达式中自动推导出来。
节点职责:每种节点类型只需要知道两件事:如何计算输出,以及在给定输出梯度的情况下如何计算相对于输入的梯度。
框架分工:现代框架负责处理复杂的反向传播逻辑,而开发者通常只需要手写特定层(Layer)或节点(Node)的局部导数即可。

3. 代码实现 API
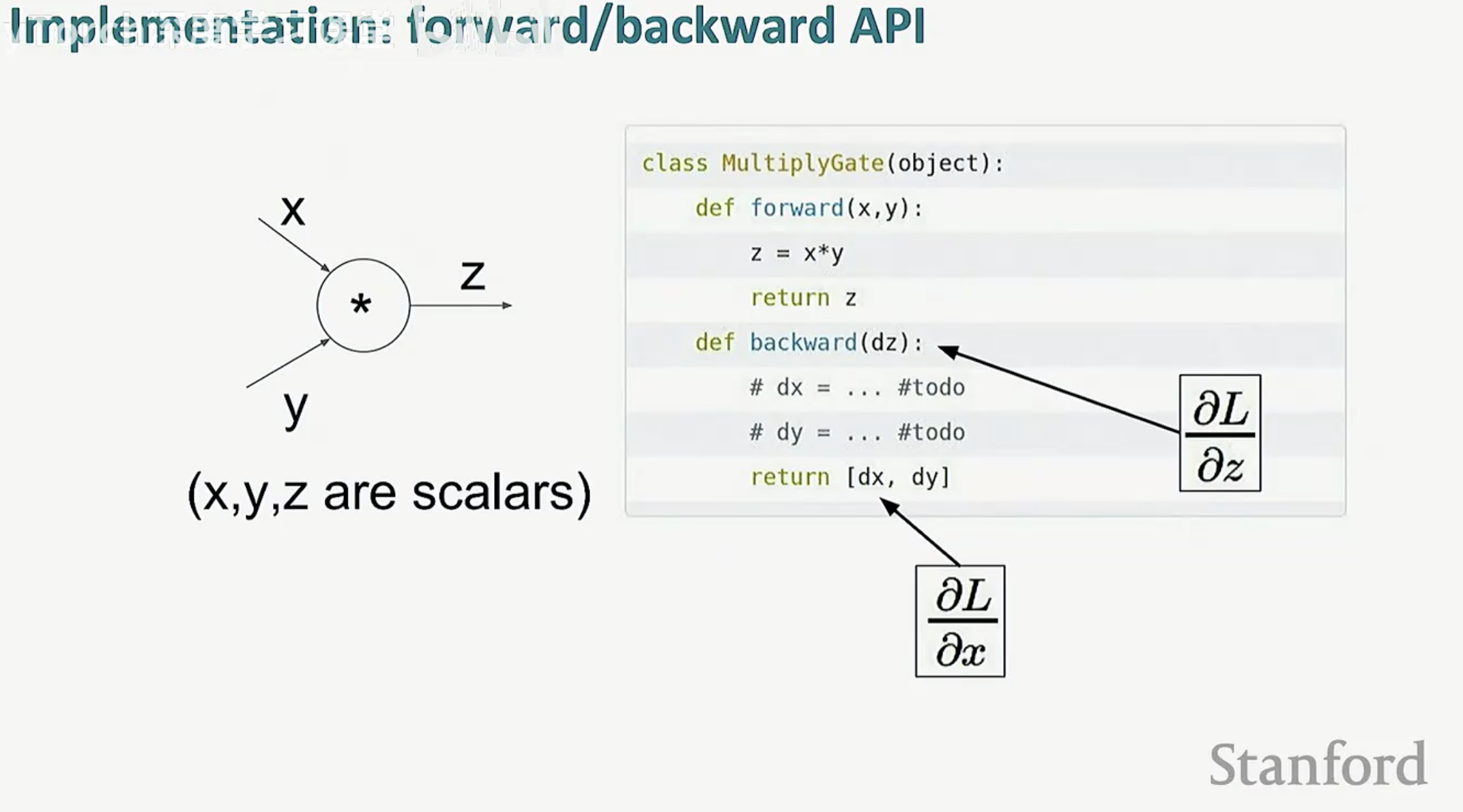
在底层代码实现中,每个功能模块通常被封装为一个具有 forward 和 backward 接口的类。以乘法门(MultiplyGate)为例:

4. 数值梯度检查(Numeric Gradient Check)
即便有了自动微分,我们在手动实现新的算子时仍可能犯错。这时,数值梯度检查就成了必备的调试手段:
原理:利用导数的定义,使用微小的步长 h(约为 1e-4)计算。
优缺点:这种方法实现简单且结果可靠,但由于需要为每一个参数重新计算 $f$,其速度非常缓慢。
应用场景:它不再用于实际训练,但在验证自定义层是否正确实现时,它是最权威的测试标准。

