第一节：从并行逻辑回归到神经网络

1. 神经网络的本质

很多人初学神经网络时会觉得它是一个复杂的“黑箱”，但从数学视角来看，神经网络并不是某种全新的魔法。本质上，一个神经网络可以看作是同时运行的多个逻辑回归。

当我们审视一个简单的单层结构时，它执行的操作与逻辑回归高度相似：对输入特征进行加权求和，然后通过一个激活函数。然而，神经网络的强大之处在于“规模”与“层级”：

• 并行计算：在同一层中，我们运行多个逻辑回归，每个逻辑回归学习数据的不同特征。

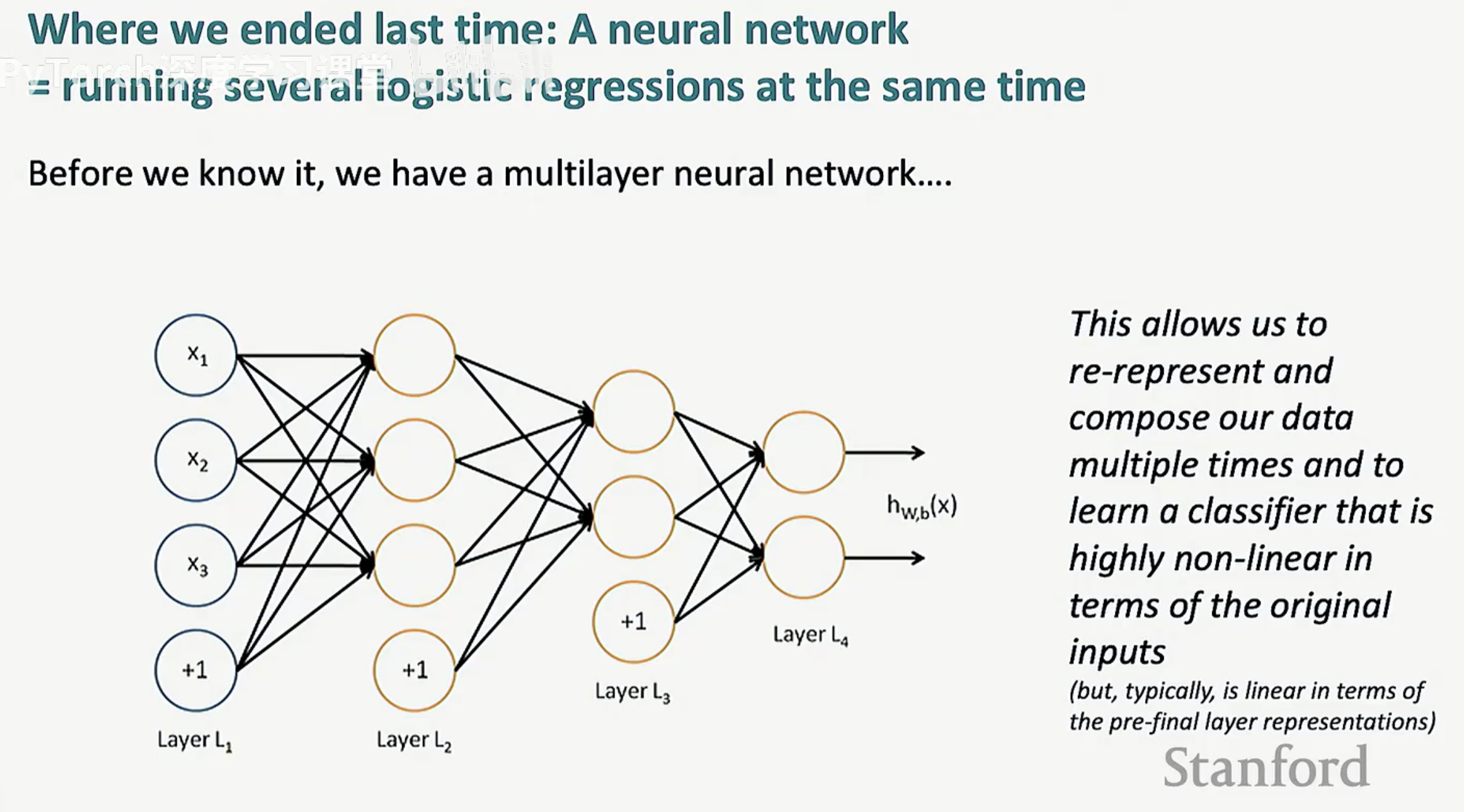
• 层级堆叠：我们将这些并行计算的结果作为下一层的输入。在不知不觉中，我们就构建出了一个多层神经网络（Multilayer Neural Network）。

2. 数据的重表示

这种层级结构（从 L₁ 到 L₄）赋予了模型一种特殊的能力：重表示（Re-representation）。

• 组合与合成：数据在穿过每一层时，都会被重新组合和合成。

• 非线性特征学习：这种多次的重表示允许模型学习到一个相对于原始输入而言高度非线性的分类器。

• 线性与非线性的统一：有趣的是，尽管最终的分类器对原始输入是非线性的，但在最后一层（Pre-final layer）的表示空间里，它通常仍然是一个线性分类器。

通过这种方式，神经网络将复杂的原始数据转化为易于分类的高层特征。

第二节：矩阵化前向传播与非线性驱动

在理解了神经网络的宏观结构后，我们需要一套高效的数学语言来描述数据如何在层与层之间流动。矩阵符号（Matrix Notation）不仅简化了书写，更是现代深度学习框架（如 PyTorch、TensorFlow）实现高性能计算的基础。

1. 矩阵化前向传播

对于神经网络中的任意一层，每一个神经元的计算都可以拆解为线性组合与激活两步。如果我们逐一列举每个神经元的公式，会得到：

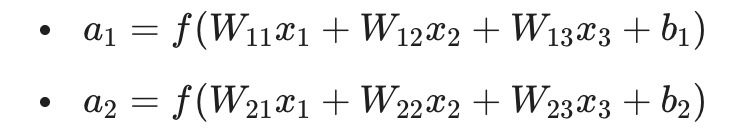
这种表达方式在层数增加时会变得极其冗长。通过矩阵化，我们可以将其浓缩为简洁的两个步骤：

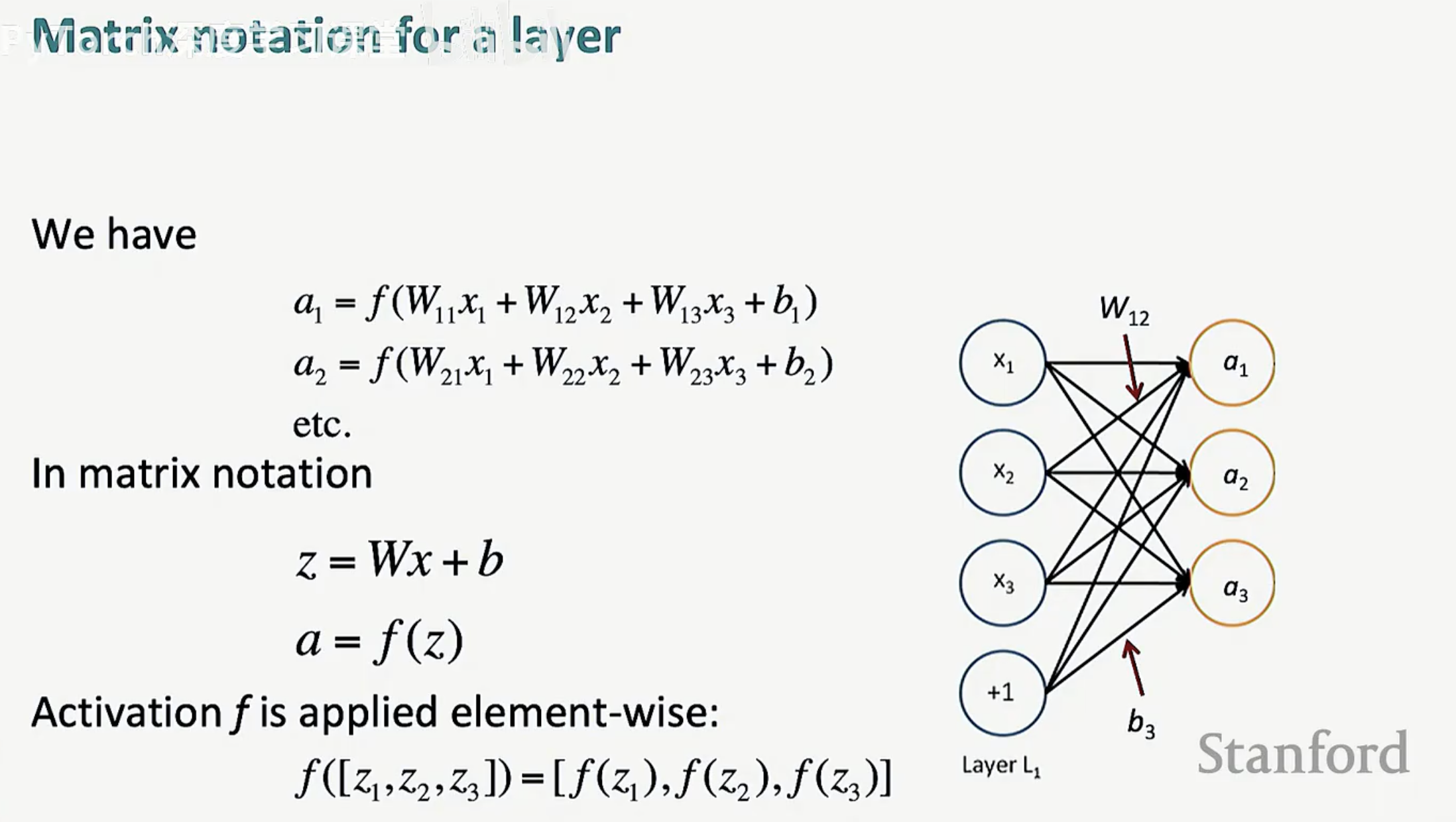
1. 线性映射：z = Wx + b

2. 非线性激活：a = f(z)

这里的激活函数 f 是逐元素（element-wise）作用于向量 z 的，即 f([z₁, z₂, z₃]) = [f(z₁), f(z₂), f(z₃)]。

2. 非线性的必要性

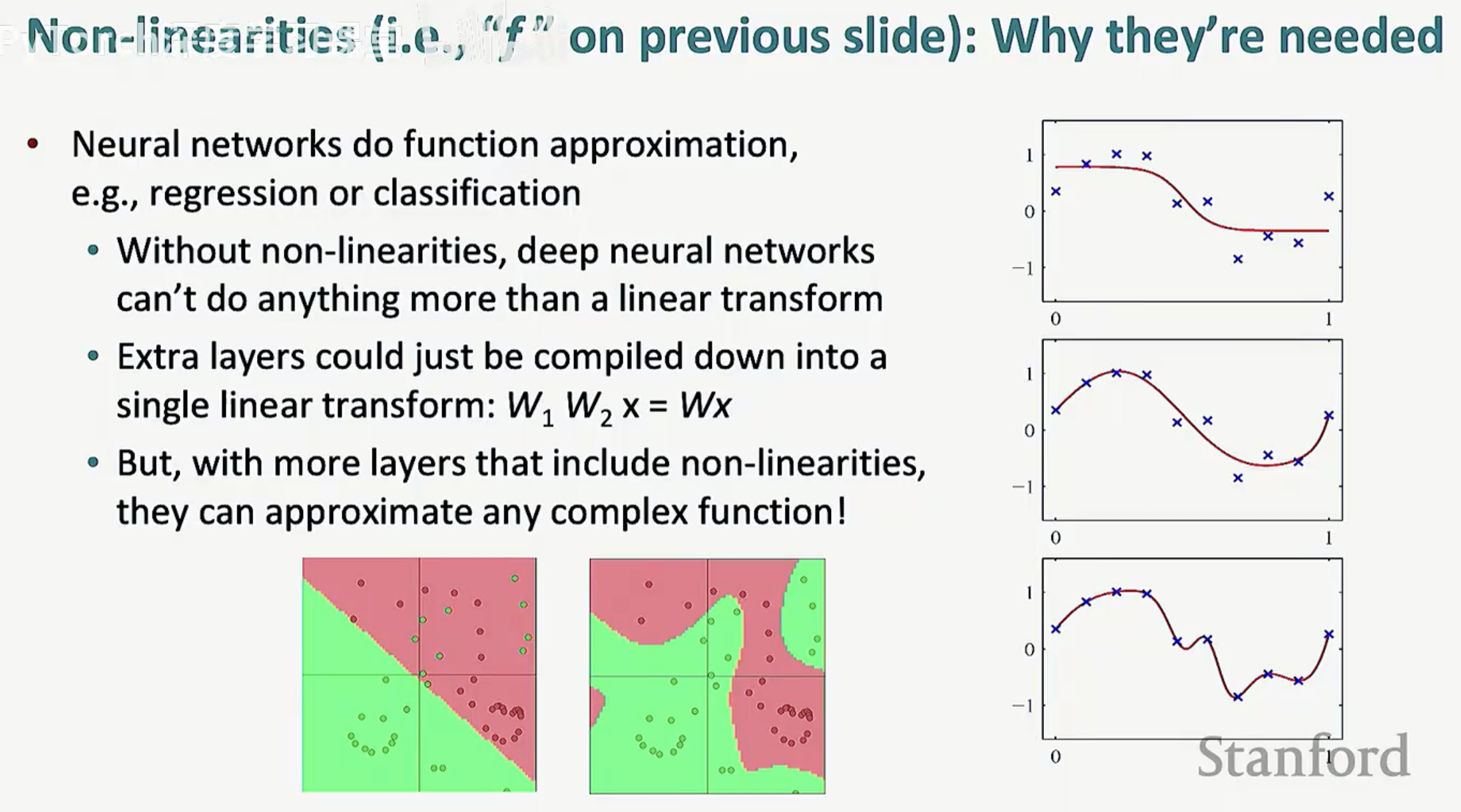
为什么我们不能只用线性层（z = Wx + b）？从数学上讲，如果没有非线性激活函数，深层神经网络将失去其存在的意义。

• 线性坍缩：多个线性层的叠加在数学上等同于一个单一的线性变换（例如 W₁W₂x = Wx）。这意味着无论你堆叠多少层，模型依然只能解决线性可分问题。

• 万能逼近：加入非线性（如 f）后，神经网络才真正具备了函数逼近（Function Approximation）的能力，能够拟合极其复杂的非线性决策边界。

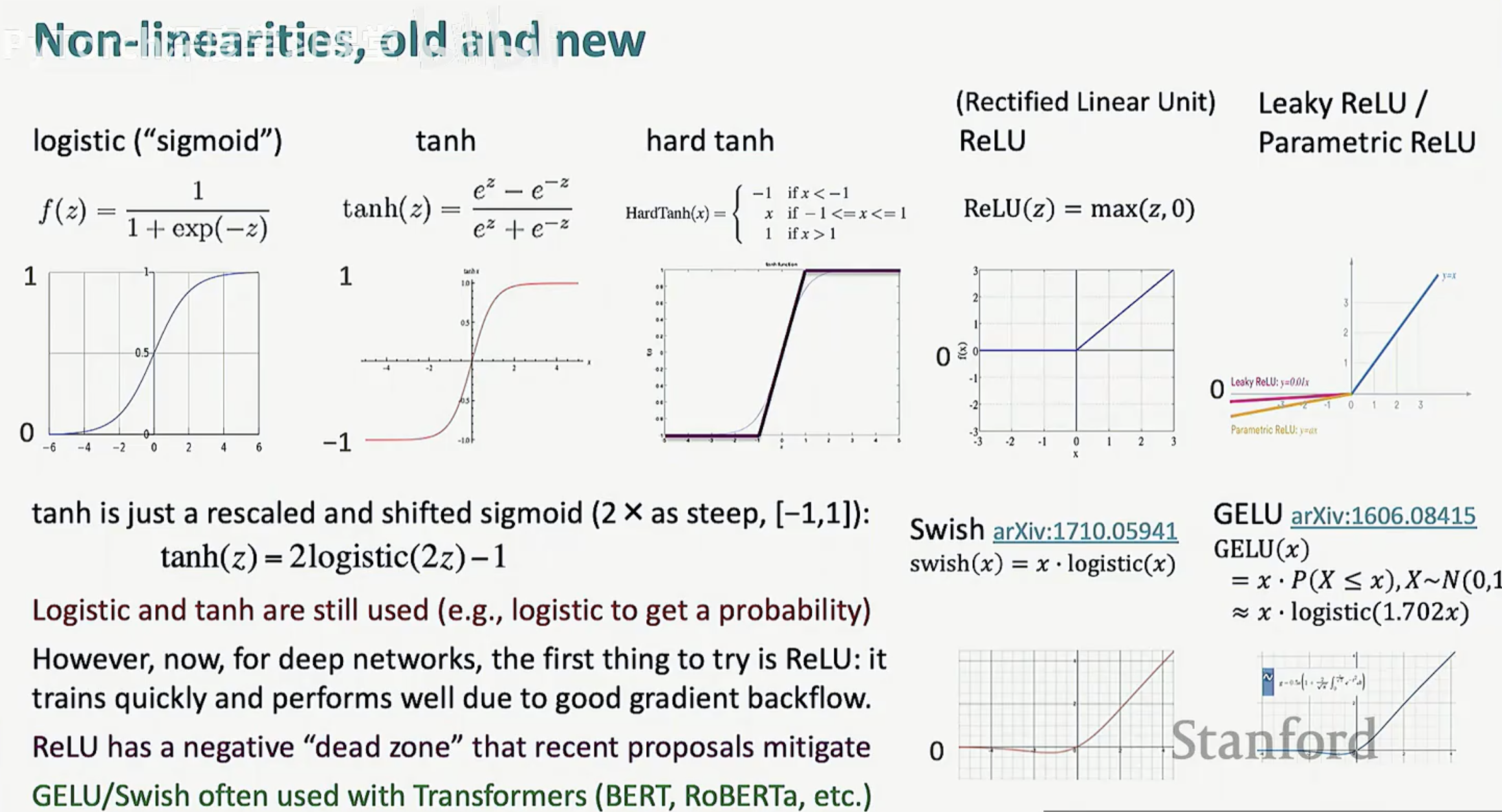
3. 激活函数：从经典到现代

随着研究的演进，激活函数的选择也经历了从生物启发到工程导向的变化：

• 经典选手：Logistic (Sigmoid) 和 Tanh。它们常用于输出层来产生概率，但在深层网络中容易导致梯度消失。

• 工业标准：ReLU (Rectified Linear Unit)。它是深层网络的首选，因为它计算简单且能有效缓解梯度衰减，使训练更高效。

• 前沿演进：Swish 和 GELU。这些变体通过引入更平滑的非线性特性，在 Transformer 等现代架构中表现优异。

第三节：NER 实战中的数据流向

为了更直观地理解上述数学公式如何转化为实际能力，我们以自然语言处理（NLP）中的经典任务——命名实体识别（NER）为例。在这个场景下，我们的目标是判断句子中的中心词是否为一个特定的实体（例如“地点”）。

1. 特征嵌入与输入映射

在 NER 任务中，单词不能直接进入数学公式，必须先转化为向量。

• 词向量嵌入：我们将中心词及其上下文窗口内的单词转化为向量并拼接，形成一个高维输入向量

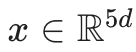
• 线性层处理：这个输入向量 x 乘以权重矩阵 W 并加上偏置 b，得到中间状态 z。

2. 隐藏层的非线性转换

数据进入隐藏层后，会经历我们之前提到的非线性变换：

• 激活计算：计算 h = f(Wx + b)，其中 f 通常选用 ReLU、Tanh 或 Sigmoid。

• 特征提取：这一步的本质是提取单词在当前语境下的深层语义特征。

3. 分数计算与概率预测

最后，模型需要给出一个“得分”，告诉我们这个词是地点的可能性有多大：

• 线性得分：通过向量内积 s = u^T h 计算出一个标量分数 s。

• 概率映射：为了进行监督学习，我们使用 Sigmoid 函数 \sigma(s) 将分数映射到 (0, 1) 区间，得到预测概率 J_t(\theta)。

如果这个词真的是地点（Location），我们希望通过训练让这个预测概率趋近于 1。

4. u 的含义：权重向量

在这一步中，u 是一个权重向量（Weight Vector）。

• 角色：它的作用类似于之前层里的权重矩阵 $W$，但因为它直接连接到最终的输出得分 $s$（一个标量），所以它通常被简化为一个向量。

• 目的：它负责将隐藏层提取到的高维特征 $h$ 进行“加权转换”，提炼出最关键的信息来决定预测结果。

5. T 的含义：转置符号

T 代表线性代数中的转置操作（Transpose）。

• 维度对齐：在标准的数学约定中，向量通常默认是“列向量”。如果我们有两个列向量 u 和 h，直接相乘是不符合矩阵乘法规则的。

• 点积运算：通过将 u 转置（从立着的列变成横着的行），u^T 就可以与列向量 h 进行矩阵乘法。

第四节：反向传播与雅可比矩阵

既然我们已经通过前向传播得到了得分 s，那么当预测出现偏差时，我们需要一套数学机制来更新参数。这就是反向传播的用武之地。

1. 梯度：灵敏度测试

梯度本质上是在问一个问题：“如果我微调输入，输出会改变多少？”

• 标量示例：对于函数 f(x) = x³，其梯度（导数）为 3x²。这意味着在 x=4 时，输出的变化率大约是输入的 48 倍。

• 多维推广：当输入变为向量 x 时，梯度就变成了一个由各个偏导数组成的向量。

2. 雅可比矩阵

如果函数不仅有多个输入，还有多个输出，我们就引入了雅可比矩阵（Jacobian Matrix）。

• 定义：一个 m X n 的矩阵，记录了 m 个输出对 n 个输入的每一个偏导数。

• 重要性：它是链式法则在高维空间的唯一语言。在计算 h = f(z) 的梯度时，由于 f 是逐元素作用的，其雅可比矩阵是一个对角矩阵，对角线上的元素正是 f'(z_i)。

3. 链式法则

反向传播其实就是雅可比矩阵的连乘。

• 通过将下游的梯度（已经算出来的误差）乘以当前的雅可比矩阵，我们就能将误差信号一路传回最开始的权重参数。

第五节：维度对齐与工程实现细节

在理解了反向传播的数学链条后，真正的挑战往往出现在代码实现阶段。当你面对成千上万维度的矩阵时，理论上的导数公式必须转化为可编程的矩阵运算。

1. 误差信号 \delta 的复用

在多层网络中，重复计算每一个梯度的开销是巨大的。为了优化性能，我们引入了误差信号（Error Signal），通常记作 \delta。

• 定义：\delta 代表了损失函数对某一输出层 z 的导数。

• 计算复用：反向传播的核心精髓在于，每一层的梯度都可以通过上一层传回的 \delta 与当前层的雅可比矩阵相乘得到。这种“下游乘上游”的策略避免了大量的重复求导运算。

2. 维度对齐惯例（Shape Convention）

在数学推导中，雅可比矩阵可能是一个巨大的、稀疏的 m X n 矩阵，但在深度学习工程实现（如 PyTorch）中，我们遵循一个硬性准则：参数的梯度形状必须与其本身的形状完全一致。

• 矩阵求导技巧：当我们计算损失对权重矩阵 W 的导数时，不能简单套用标量公式。

• 外积的应用：例如，对于线性层 z = Wx + b，经过推导和维度对齐，你会发现最终用于更新 W 的梯度公式是 \delta x^T。这种通过转置（T）实现的维度匹配，确保了梯度可以直接累加到参数矩阵上。

3. 逐元素函数的特殊性

正如我们在前向传播中看到的，激活函数是逐元素作用的。在反向传播时，这意味着它的雅可比矩阵是一个对角矩阵（Diagonal Matrix）。

• 计算简化：在编程实现中，我们不需要真的创建一个庞大的对角矩阵，只需要将传入的梯度与激活函数的导数 f'(z) 进行逐元素相乘（Hadamard Product）即可。