一、K-means算法的定义
K-means算法是一种经典的聚类算法,它通过将数据划分为K个簇来实现聚类目标。算法的核心思想是通过迭代优化簇中心的位置,使得簇内的数据点尽可能接近簇中心,而不同簇之间的数据点尽可能远离。
通俗理解:
就好像是在一个操场上把一群乱跑的小孩分成几个小组,让每个小组里的小孩尽量靠近自己的组长,而不同小组之间的小孩尽量拉开距离。这个过程会不断重复调整,直到找到最合适的分组方式,让每个小组都尽可能地紧密。
二、K-means算法直观理解
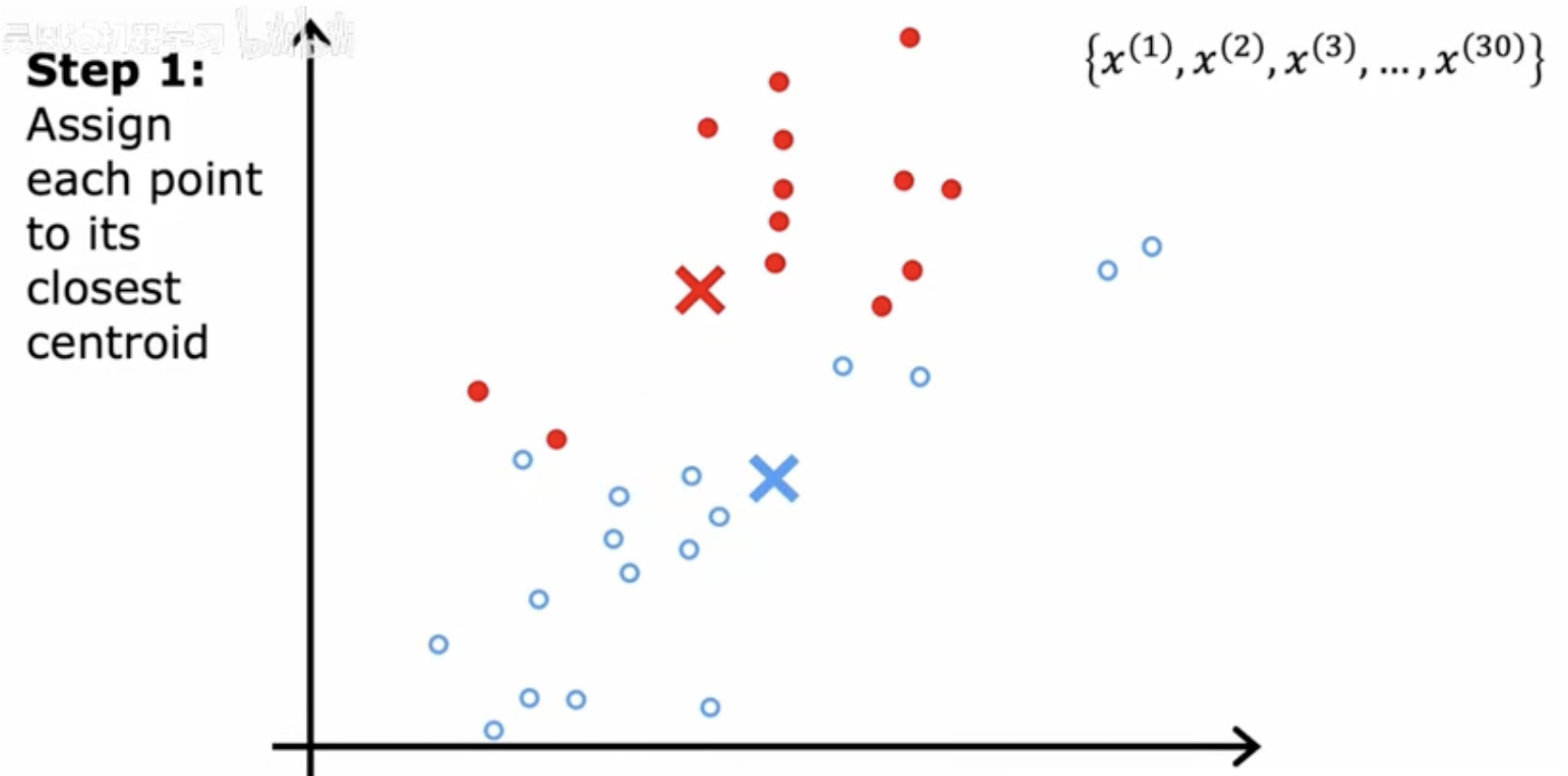
步骤1 - 分配数据点到最近的中心点

这张图展示了K-means算法的第一步,即“分配”阶段。在这个阶段,每个数据点(图中黄色点)被分配到最近的簇中心(图中红色和蓝色点)。每个数据点根据其与簇中心的距离来决定归属的簇。图中黑色箭头表示数据点到其最近簇中心的分配路径。
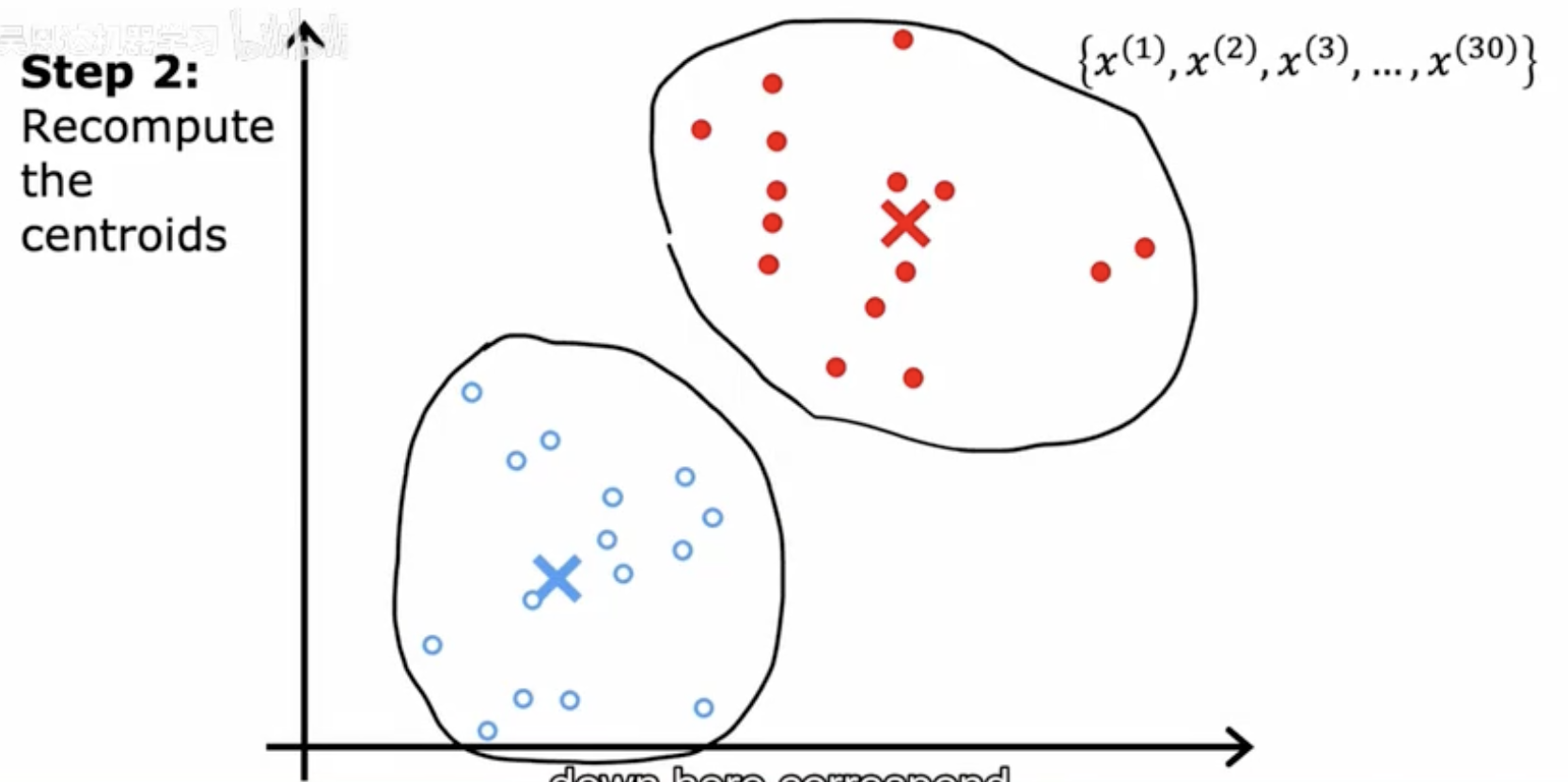
步骤2 - 重新计算簇中心
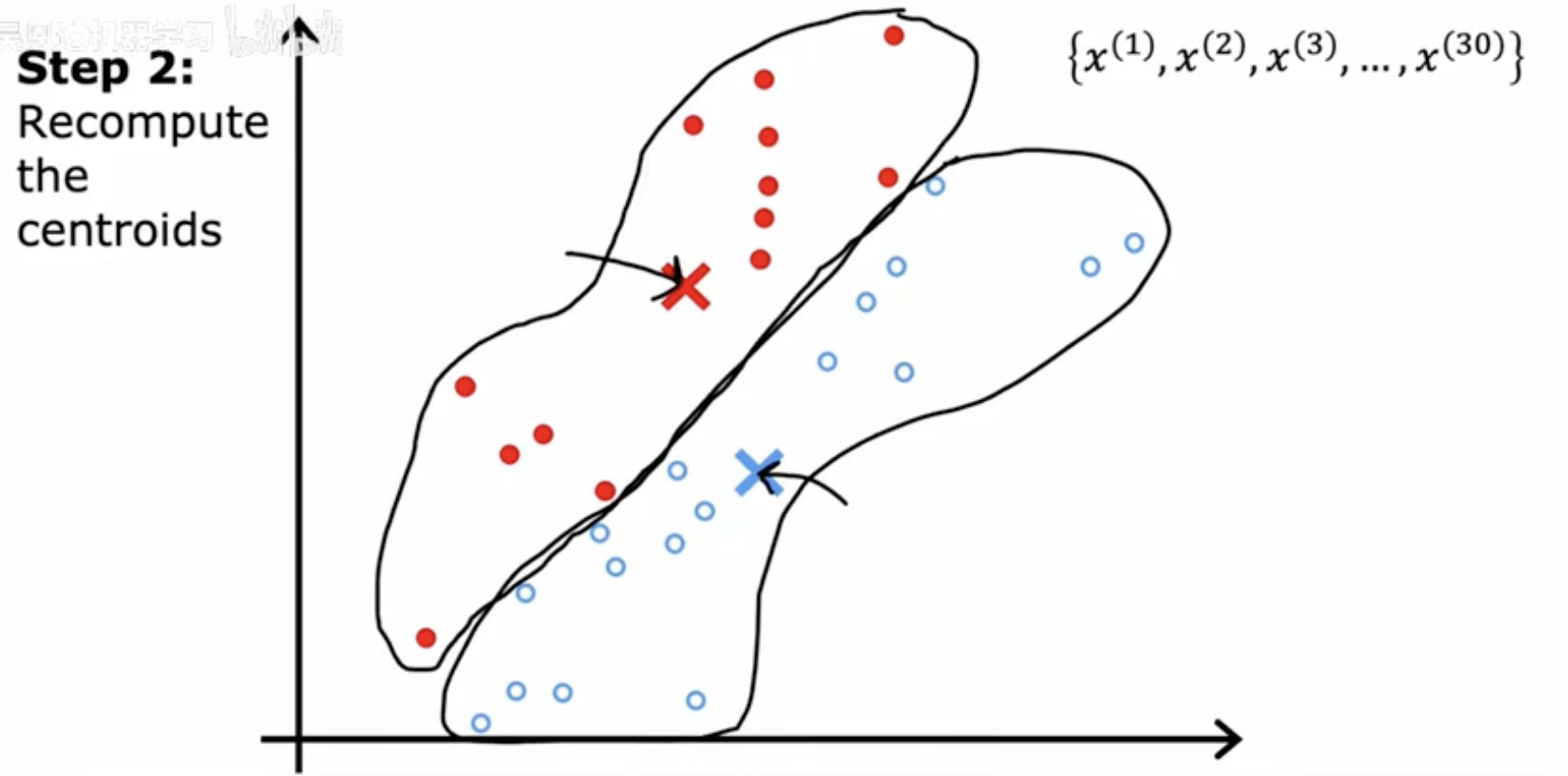
这张图展示了K-means算法的第二步,即“重新计算”阶段。在这个阶段,一旦所有数据点都被分配到相应的簇中,算法会重新计算每个簇的中心点。簇中心被定义为该簇所有点的平均位置。图中黑色轮廓线表示重新计算后的新簇边界,而簇中心(红色和蓝色点)根据簇内所有点的平均位置进行了更新。
步骤3 - 后续迭代直至收敛

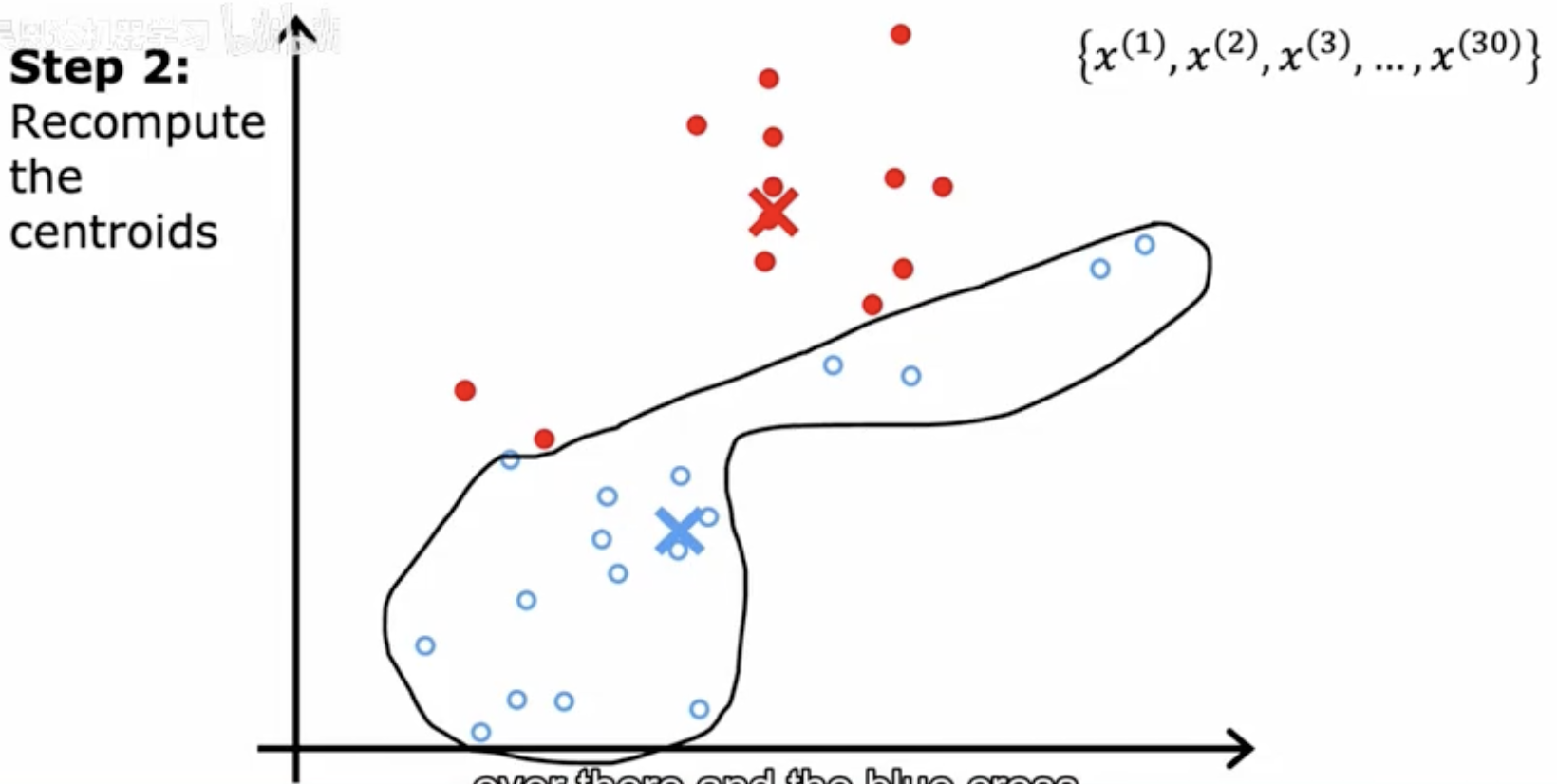
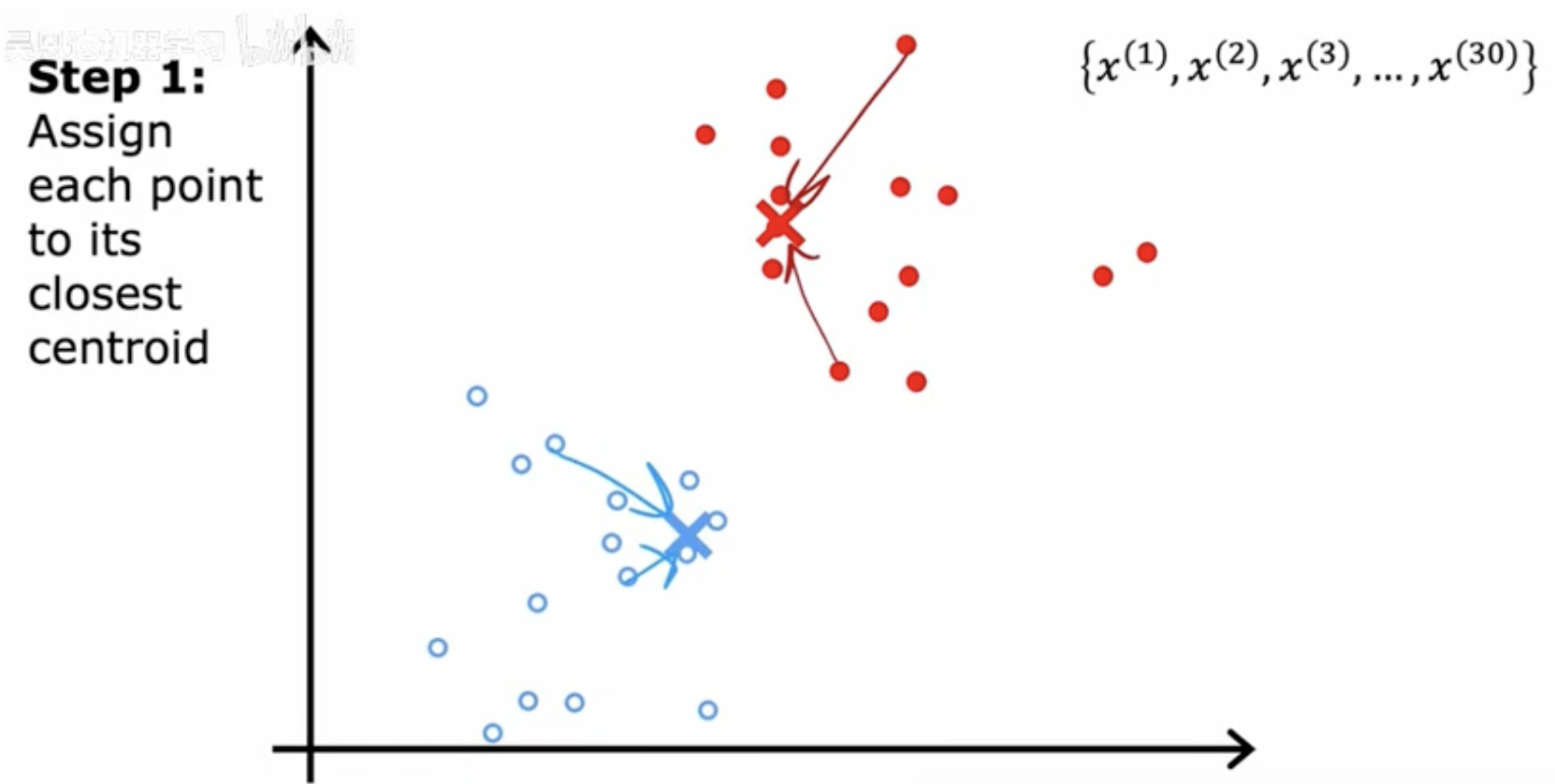
在后续的迭代中,算法继续重复步骤1和步骤2,即重新分配点到最近的簇中心,然后再次重新计算簇中心。这个过程会一直持续,直到簇中心的位置不再有显著变化,或者达到预设的迭代次数,从而完成聚类过程。图中展示了簇中心的进一步优化和簇边界的调整,直到算法收敛。
三、K-means算法流程与示例图解

这幅图片展示了K-means算法的伪代码和对应的示意图。
左侧是K-means算法的伪代码:
首先,随机初始化K个簇中心(μ1, μ2, ..., μK)。
然后,进入一个重复执行的循环:
分配步骤:对于每个数据点x(i),找到最近的簇中心,并将其分配给该簇(c(i)表示x(i)最近的簇中心的索引)。
移动步骤:对于每个簇k,重新计算簇中心μk,它是该簇所有已分配点的平均值。
右侧是K-means算法的示意图:
图中显示了二维空间上的一些数据点(黑色点),以及两个簇中心(红色叉号)。
每个簇中心用一个圆圈表示其簇的边界,圆圈内的点属于该簇。
红色圆圈和蓝色圆圈分别代表两个簇,簇中心用红色和蓝色叉号表示。
图中还标注了n=2和K=2,表示数据点的维度为2,簇的数量为2。
公式μ1 = 1/4[x(1) + x(5) + x(6) + x(10)]展示了如何计算簇1的中心点,即簇内四个点的平均位置。
特殊情况:

右侧的示意图中,大部分数据点(黑色点)已经被分配到了两个簇中,分别由红色和蓝色圆圈表示。然而,有一个数据点(位于x1和x2之间的黑色点)没有被包含在任何一个圆圈内,这表明它没有被分配到任何簇中。
这种情况可能是由于算法初始化时簇中心选择不当或者数据点的分布特性导致的。在实际应用中,这种情况可能需要通过调整算法参数(如簇的数量K)或者使用其他聚类方法来解决。
四、K-means算法在处理不完全分离簇时的挑战
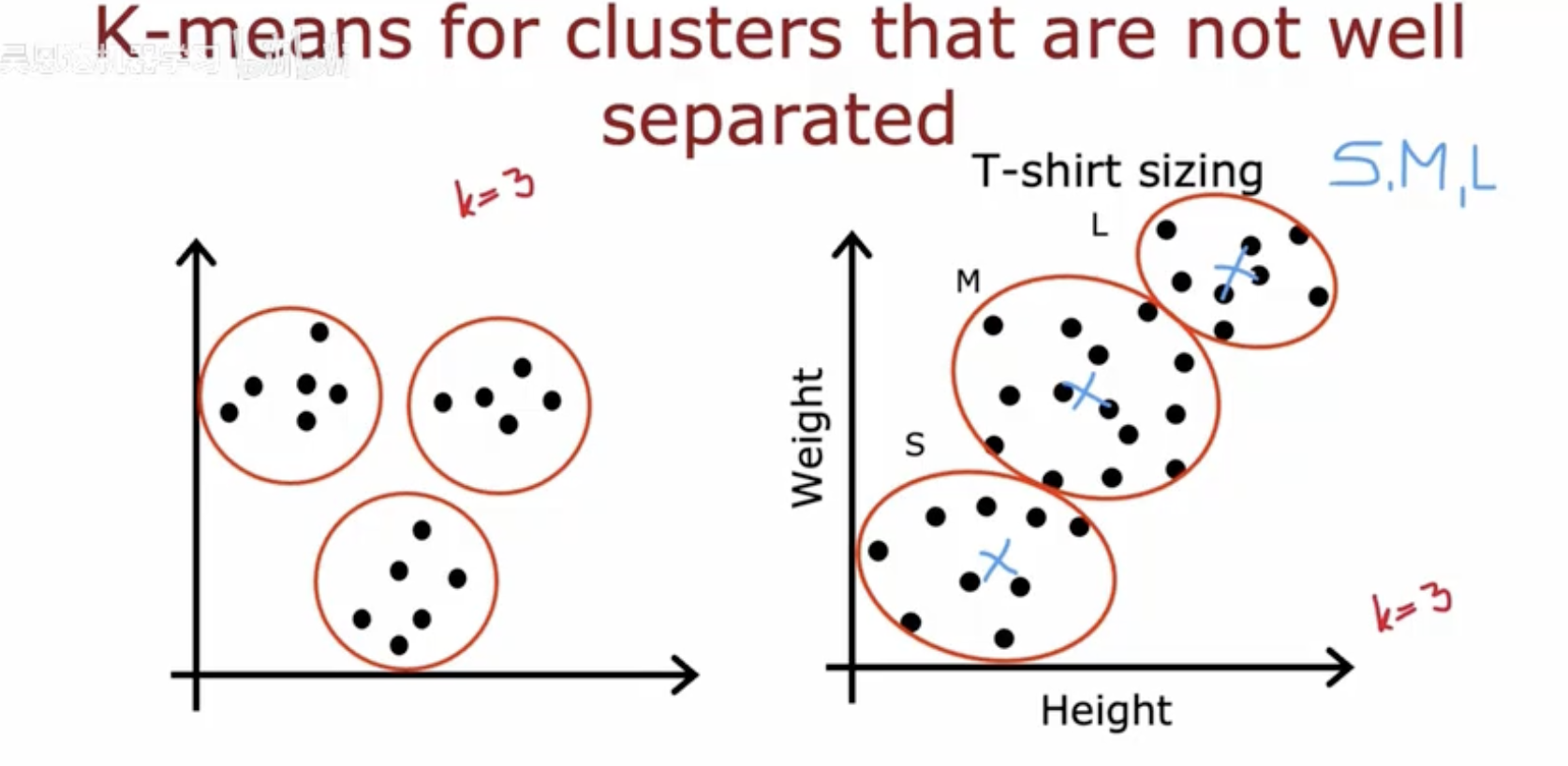
左侧图示:
显示了在二维空间中,K-means算法试图将数据点分为3个簇(k=3)。
每个簇用一个圆圈表示,圆圈内的点属于同一个簇。
尽管数据点被分成了3个簇,但这些簇之间并没有明显的边界,说明簇之间不是完全分离的。
右侧图示:
展示了一个更实际的例子,即根据身高和体重来对T恤尺寸进行聚类(k=3)。
圆圈代表不同的T恤尺寸(S, M, L),每个尺寸对应一个簇。
簇中心用叉号表示,代表该尺寸簇内点的平均身高和体重。
由于身高和体重数据的重叠,导致某些簇之间的边界不清晰,这可能会影响K-means算法聚类的效果。
总体来说,这幅图说明了K-means算法在处理不完全分离的簇时可能会遇到的问题,即簇之间的边界可能不够明确,导致聚类结果不理想。
